Chapter 25
3D Alpha Shapes

Assume we are given a set $$S of points in 2D or 3D and we'd like to have something like ``the shape formed by these points.'' This is quite a vague notion and there are probably many possible interpretations, the alpha shape being one of them. Alpha shapes can be used for shape reconstruction from a dense unorganized set of data points. Indeed, an alpha shape is demarcated by a frontier, which is a linear approximation of the original shape [BB97].

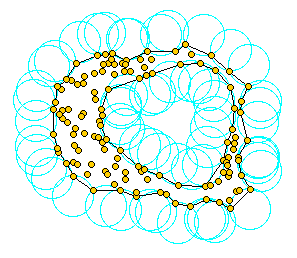
As mentionned in Edelsbrunner's and Mücke's paper [EM94], one can intuitively think of an alpha shape as the following. Imagine a huge mass of ice-cream making up the space $$ ³ and containing the points as ``hard'' chocolate pieces. Using one of those sphere-formed ice-cream spoons we carve out all parts of the ice-cream block we can reach without bumping into chocolate pieces, thereby even carving out holes in the inside (eg. parts not reachable by simply moving the spoon from the outside). We will eventually end up with a (not necessarily convex) object bounded by caps, arcs and points. If we now straighten all ``round'' faces to triangles and line segments, we have an intuitive description of what is called the alpha shape of $$S. Here's an example for this process in 2D (where our ice-cream spoon is simply a circle):

Alpha shapes depend on a parameter $$ from which they are named. What is $$ in the ice-cream game? $$ is the squared radius of the carving spoon. A very small value will allow us to eat up all of the ice-cream except the chocolate points themselves. Thus we already see that the alpha shape degenerates to the point-set $$S for $$ 0. On the other hand, a huge value of $$ will prevent us even from moving the spoon between two points since it's way too large. So we will never spoon up ice-cream lying in the inside of the convex hull of $$S, and hence the alpha shape for $$ is the convex hull of $$S.¹

25.1   Definitions

More precisely, the definition of alpha shapes is based on an underlying triangulation that may be a Delaunay triangulation in case of basic alpha shapes or a regular triangulation (cf. 22.3) in case of weighted alpha shapes.

Let us consider the basic case with a Delaunay triangulation. We first define the alpha complex of the set of points $$S. The alpha complex is a subcomplex of the Delaunay triangulation. For a given value of $$, the alpha complex includes all the simplices in the Delaunay triangulation which have an empty circumsphere with squared radius equal or smaller than $$. Here ``empty'' means that the open sphere do not include any points of $$S. The alpha shape is then simply the domain covered by the simplices of the alpha complex (see [EM94]).

In general, an alpha complex is a non-connected and non-pure complex. This means in particular that the alpha complex may have singular faces. For $$0 k d-1, a $$k-simplex of the alpha complex is said to be singular if it is not a facet of a $$(k+1)-simplex of the complex CGAL provides two versions of the alpha shapes. In the general mode, the alpha shapes correspond strictly to the above definition. The regularized mode provides a regularized version of the alpha shapes corresponding to the domain covered by a regularized version of the alpha complex where singular faces are removed.

The alpha shapes of a set of points $$S form a discrete family, even though they are defined for all real numbers $$. The entire family of alpha shapes can be represented through the underlying triangulation of $$S. In this representation each $$k-simplex of the underlying triangulation is associated with an interval that specifies for which values of $$ the $$k-simplex belongs to the alpha complex. Relying on this fact, the family of alpha shapes can be computed efficiently and relatively easily. Furthermore, we can select the optimal value of $$ to get an alpha shape including all data points and having less than a given number of connected components. Also, the alpha-values allows to define a filtration on the faces of the triangulation of a set of points. In this filtration, the faces of the triangulation are output in increasing order of the alpha value for which they appear in the alpha complex. In case of equal alpha value lower dimensional faces are output first.

The definition is analog in the case of weigthed alpha shapes. The input set is now a set of weighted points (which can be regarded as spheres) and the underlying triangulation is the regular triangulation of this set. Two spheres, or two weighted points , with centers $$C₁, C₂ and radii $$r₁, r₂ are said to be orthogonal iff $$ C₁C₂ ² = r₁² + r₂² and suborthogonal iff $$ C₁C₂ ² < r₁² + r₂². For a given value of $$ the weighted alpha complex is formed with the simplices of the regular triangulation triangulation such that there is a sphere orthogonal to the weighted points associated with the vertices of the simplex and suborthogonal to all the other input weighted points. Once again the alpha shape is then defined as the domain covered by a the alpha complex and arise in two versions general or regularized.

25.2   Functionality

The class CGAL::Alpha_shape_3<Dt> represents the whole family of alpha shapes for a given set of points. The class includes the underlying triangulation Dt of the set, and associates to each $$k-face of this triangulation an interval specifying for which values of $$ the face belongs to the alpha complex.

The class CGAL::Alpha_shape_3<Dt> provides functions to set and get the current $$-value, as well as an iterator that enumerates the $$ values where the alpha shape changes.

The class provides member functions to classify for a given value of $$alpha the different faces of the triangulation as EXTERIOR, SINGULAR, REGULAR or INTERIOR with respect to the alpha shape. A $$k face on the boundary of the alpha complex is said to be REGULAR if it is a subface of the alpha complex which is a subface of some $$k+1 face of the alpha complex and SINGULAR otherwise.

The class provides also output iterators to get for a given $$alpha value the vertices, edges, facets and cells of the different types (EXTERIOR, SINGULAR, REGULAR or INTERIOR).

Also the class has a filtration member function that, given an output iterator with CGAL::object as value type, outputs the faces of the triangulation according to the order of apparition in the alpha complex when alpha increases.

Finally, it provides a function to determine the smallest value $$ such that the alpha shape satisfies the following two properties 
(ii) all data points are either on the boundary or in the interior of the regularized version of the alpha shape (no singular faces).
(i) The number of components is equal or less than a given number .

The current implementation is static, that is after its construction points cannot be inserted or removed.

25.3   Concepts and Models

We currently do not specify concepts for the underlying triangulation type. Models that work for a basic alpha-shape are the classes CGAL::Delaunay_triangulation_3 and CGAL::Triangulation_hierarchy_3 templatized with a Delaunay triangulation. A model that works for a weighted alpha-shape is the class CGAL::Regular_triangulation_3.

The triangulation needs a geometric traits class as argument. The requirements of this class are described in the concept CGAL::AlphaShapeTraits_3 for which the CGAL kernels are models in the non-weighted case, and for which the class CGAL::Weighted_alpha_shape_euclidean_traits_3 is model in the weighted case.

The triangulation data structure of the triangulation with any has to be a model of the concept CGAL::TriangulationDataStructure_3. However it must be parameterized with vertex and cell classes, which are model of the concepts AlphaShapeVertex_3 and AlphaShapeCell_3. The package provides by default the classes CGAL::Alpha_shape_vertex_base_3<Gt> and CGAL::Alpha_shape_cell_base_3<Gt>.

25.4   Examples

25.4.1   Example for Basic Alpha-Shapes

This example builds a basic alpha shape using a Delaunay triangulation as underlying triangulation.

// examples/Alpha_shapes_3/example_alpha.C

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/Alpha_shape_3.h>

#include <fstream>
#include <list>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};

typedef CGAL::Alpha_shape_vertex_base_3<K>          Vb;
typedef CGAL::Alpha_shape_cell_base_3<K>            Fb;
typedef CGAL::Triangulation_data_structure_3<Vb,Fb> Tds;
typedef CGAL::Delaunay_triangulation_3<K,Tds>       Triangulation_3;
typedef CGAL::Alpha_shape_3<Triangulation_3>        Alpha_shape_3;

typedef K::Point_3                                  Point;
typedef Alpha_shape_3::Alpha_iterator               Alpha_iterator;

int main()
{
  std::list<Point> lp;

  //read input
  std::ifstream is("./data/bunny_1000");
  int n;   
  is >> n;
  std::cout << "Reading " << n << " points " << std::endl; 
  Point p;
  for( ; n>0 ; n--)    { 
    is >> p;      
    lp.push_back(p);
  }
  
  // compute alpha shape  
  Alpha_shape_3 as(lp.begin(),lp.end());
  std::cout << "Alpha shape computed in REGULARIZED mode by defaut" 
	    << std::endl;

  // find optimal alpha value
  Alpha_iterator opt = as.find_optimal_alpha(1);
  std::cout << "Optimal alpha value to get one connected component is " 
	    <<  *opt    << std::endl;
  as.set_alpha(*opt);
  assert(as.number_of_solid_components() == 1);
  return 0;
}

25.4.2   Building Basic Alpha Shapes for Many Points

// examples/Alpha_shapes_3/example_big_alpha.C

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/Triangulation_hierarchy_3.h>
#include <CGAL/Alpha_shape_3.h>

#include <fstream>
#include <list>

struct K : CGAL::Exact_predicates_inexact_constructions_kernel {};

typedef CGAL::Alpha_shape_vertex_base_3<K>               Vb;
typedef CGAL::Triangulation_hierarchy_vertex_base_3<Vb>  Vbh;
typedef CGAL::Alpha_shape_cell_base_3<K>                 Fb;
typedef CGAL::Triangulation_data_structure_3<Vbh,Fb>     Tds;
typedef CGAL::Delaunay_triangulation_3<K,Tds>            Delaunay;
typedef CGAL::Triangulation_hierarchy_3<Delaunay>        Delaunay_hierarchy;
typedef CGAL::Alpha_shape_3<Delaunay_hierarchy>          Alpha_shape_3;

typedef K::Point_3                                  Point;
typedef Alpha_shape_3::Alpha_iterator               Alpha_iterator;
typedef Alpha_shape_3::NT                           NT;

int main()
{
  Delaunay_hierarchy dt;
  std::ifstream is("./data/bunny_1000");
  int n;
  is >> n;
  Point p;
  std::cout << n << " points read" << std::endl;
  for( ; n>0 ; n--) {
    is >> p;
    dt.insert(p);
  }
  std::cout << "Delaunay computed." << std::endl;

  // compute alpha shape  
  Alpha_shape_3 as(dt);
  std::cout << "Alpha shape computed in REGULARIZED mode by defaut." 
	    << std::endl;

   // find optimal alpha values
  Alpha_shape_3::NT alpha_solid = as.find_alpha_solid();
  Alpha_iterator opt = as.find_optimal_alpha(1);
  std::cout << "Smallest alpha value to get a solid through data points is " 
	    << alpha_solid << std::endl;
  std::cout << "Optimal alpha value to get one connected component is " 
	    <<  *opt    << std::endl;
  as.set_alpha(*opt);
  assert(as.number_of_solid_components() == 1);
  return 0;
}

25.4.3   Example for Weighted Alpha-Shapes

The following examples build a weighted alpha shape requiring a regular triangulation as underlying triangulation. The alpha shape is build in GENERAL mode.

// examples/Alpha_shapes_3/example_weight.C

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Weighted_alpha_shape_euclidean_traits_3.h>
#include <CGAL/Regular_triangulation_3.h>
#include <CGAL/Alpha_shape_3.h>
#include <list>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K;

typedef CGAL::Weighted_alpha_shape_euclidean_traits_3<K> Gt;

typedef CGAL::Alpha_shape_vertex_base_3<Gt>         Vb;
typedef CGAL::Alpha_shape_cell_base_3<Gt>           Fb;
typedef CGAL::Triangulation_data_structure_3<Vb,Fb> Tds;
typedef CGAL::Regular_triangulation_3<Gt,Tds>       Triangulation_3;
typedef CGAL::Alpha_shape_3<Triangulation_3>        Alpha_shape_3;

typedef Alpha_shape_3::Cell_handle          Cell_handle;
typedef Alpha_shape_3::Vertex_handle        Vertex_handle;
typedef Alpha_shape_3::Facet                Facet;
typedef Alpha_shape_3::Edge                 Edge;
typedef Gt::Weighted_point                  Weighted_point;
typedef Gt::Bare_point                      Bare_point;

int main()
{
  std::list<Weighted_point> lwp;

  //input : a small molecule
  lwp.push_back(Weighted_point(Bare_point( 1, -1, -1), 4));
  lwp.push_back(Weighted_point(Bare_point(-1,  1, -1), 4));
  lwp.push_back(Weighted_point(Bare_point(-1, -1,  1), 4));
  lwp.push_back(Weighted_point(Bare_point( 1,  1,  1), 4));
  lwp.push_back(Weighted_point(Bare_point( 2,  2,  2), 1));

  //build alpha_shape  in GENERAL mode and set alpha=0
  Alpha_shape_3  as(lwp.begin(), lwp.end(), 0, Alpha_shape_3::GENERAL);

  //explore the 0-shape - It is dual to the boundary of the union.
  std::list<Cell_handle> cells;
  std::list<Facet>       facets;
  std::list<Edge>        edges;
  as.get_alpha_shape_cells(std::back_inserter(cells),
			   Alpha_shape_3::INTERIOR);
  as.get_alpha_shape_facets(std::back_inserter(facets),
			    Alpha_shape_3::REGULAR);
  as.get_alpha_shape_facets(std::back_inserter(facets),
			    Alpha_shape_3::SINGULAR);
  as.get_alpha_shape_edges(std::back_inserter(edges),
			   Alpha_shape_3::SINGULAR);
  std::cout << " The 0-shape has : " << std::endl;
  std::cout << cells.size() << " interior tetrahedra" << std::endl;
  std::cout << facets.size() << " boundary facets" << std::endl;
  std::cout << edges.size()  << " singular edges" << std::endl;
  return 0;
}

Footnotes

1	ice cream, ice cream!!! The wording of this introductory paragraphs is borrowed from Kaspar Fischer's `` Introduction to Alpha Shapes'' which can be found at http://n.ethz.ch/student/fischerk/alphashapes/as/index.html. The picture has been taken from Walter Luh's homepage at http://www.stanford.edu/&wtilde;luh/cs448b/alphashapes.html.