2D Boolean Operations on Nef Polygons Embedded on the Sphere Reference

Peter Hachenberger and Lutz Kettner

This package offers the equivalent to 2D Nef Polygons in the plane. Here halfplanes correspond to half spheres delimited by great circles.

Introduced in: CGAL 3.1
Depends on: 2D Boolean Operations on Nef Polygons
BibTeX: cgal:hk-bonpes2-18b
License: GPL

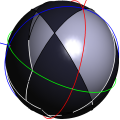
Nef polyhedra are defined as a subset of the d-dimensional space obtained by a finite number of set complement and set intersection operations on halfspaces.

Due to the fact that all other binary set operations like union, difference and symmetric difference can be reduced to intersection and complement calculations, Nef polyhedra are also closed under those operations. Also, Nef polyhedra are closed under topological unary set operations. Given a Nef polyhedron one can determine its interior, its boundary, and its closure.

Additionally, a d-dimensional Nef polyhedron has the property, that its boundary is a (d-1)-dimensional Nef polyhedron. This property can be used as a way to represent 3-dimensional Nef polyhedra by means of planar Nef polyhedra. This is done by intersecting the neighborhood of a vertex in a 3D Nef polyhedron with an \( \epsilon\)-sphere. The result is a planar Nef polyhedron embedded on the sphere.

The intersection of a halfspace going through the center of the \( \epsilon\)-sphere, with the \( \epsilon\)-sphere, results in a halfsphere which is bounded by a great circle. A binary operation of two halfspheres cuts the great circles into great arcs.

The incidence structure of planar Nef polyhedra can be reused. The items are denoted as svertex, shalfedge and sface, analogous to their counterparts in CGAL::Nef_polyhedron_2. Additionally, there is the shalfloop representing the great circles.

Classified Reference Pages

Classes
class	CGAL::Nef_polyhedron_S2< Traits >
	An instance of data type Nef_polyhedron_S2<Traits> is a subset of the sphere \( S_2\) that is the result of forming complements and intersections starting from a finite set H of halfspaces bounded by a plane containing the origin. More...
class	CGAL::Nef_polyhedron_S2< Traits >::Sphere_circle
	An object c of type Sphere_circle is an oriented great circle on the surface of a unit sphere. More...
class	CGAL::Nef_polyhedron_S2< Traits >::Sphere_point
	An object p of type Sphere_point<R> is a point on the surface of a unit sphere. More...
class	CGAL::Nef_polyhedron_S2< Traits >::Sphere_segment
	An object s of type Sphere_segment is a segment in the surface of a unit sphere that is part of a great circle trough the origin. More...
class	CGAL::Nef_polyhedron_S2< Traits >::SFace_cycle_iterator
	The type SFace_cycle_iterator iterates over a list of Object_handles. More...
class	CGAL::Nef_polyhedron_S2< Traits >::SFace
	Figures figureNefS2SVertexIncidences and figureNefS2SHalfloopIncidences illustrate the incidences of an sface. More...
class	CGAL::Nef_polyhedron_S2< Traits >::SHalfedge
	A shalfedge is a great arc on a sphere map. More...
class	CGAL::Nef_polyhedron_S2< Traits >::SHalfloop
	A sloop is a great circle on a sphere. More...
class	CGAL::Nef_polyhedron_S2< Traits >::SVertex
	Figure figureNefS2SVertexIncidences illustrates the incidence of a svertex on a sphere map. More...