2D Hyperbolic Delaunay Triangulations Reference

Mikhail Bogdanov, Iordan Iordanov, and Monique Teillaud

This package enables building and handling Delaunay triangulations of point sets in the Poincaré disk model of the hyperbolic plane. Triangulations are built incrementally and can be modified by insertion and removal of vertices; point location facilities are also offered, as well as primitives to build the dual Voronoi diagrams.

Introduced in: CGAL 4.14
Depends on: 2D Triangulation
BibTeX: cgal:bt-ht2-17-19a
License: GPL
Windows Demo: Hyperbolic Delaunay Triangulation
Common Demo Dlls: dlls

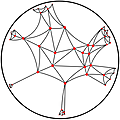
The Delaunay triangulation of a set of points \(P\) in the hyperbolic plane \(\mathbb H^2\) is a two-dimensional connected simplicial complex with vertex set defined by the points \(P\).

Classified Reference Pages

Concepts

• HyperbolicDelaunayTriangulationTraits_2 describes the requirements for an interface for geometric objects, constructions, and predicates in the hyperbolic plane.
• HyperbolicTriangulationFaceBase_2 describes the requirements for faces of the hyperbolic Delaunay triangulation to be filtered from the faces of the Euclidean Delaunay triangulation.

Classes

• CGAL::Hyperbolic_Delaunay_triangulation_2 is the main class of the 2D Hyperbolic Triangulation package. It enables the constructions of Delaunay triangulations in the hyperbolic plane. It offers all the functionalities provided by CGAL::Delaunay_triangulation_2, such as point location, insertion, and removal. Construction of the dual Voronoi diagram is also provided.
• CGAL::Hyperbolic_triangulation_face_base_2

Two models for the concept HyperbolicDelaunayTriangulationTraits_2 are provided:

• CGAL::Hyperbolic_Delaunay_triangulation_traits_2 is by default based upon CGAL::Exact_predicates_exact_constructions_kernel_with_sqrt and guarantees exact constructions of Delaunay triangulations and dual objects for input points with algebraic coordinates.
• CGAL::Hyperbolic_Delaunay_triangulation_CK_traits_2 is based upon CGAL::Circular_kernel_2 and guarantees exact constructions of Delaunay triangulations and dual objects when the input points have rational coordinates.

The model CGAL::Hyperbolic_Delaunay_triangulation_CK_traits_2 is faster than CGAL::Hyperbolic_Delaunay_triangulation_traits_2 for points with rational coordinates.

Modules
	Concepts
	Main Classes
	Traits Classes
	Face Classes