3D Boolean Operations on Nef Polyhedra Reference

Peter Hachenberger and Lutz Kettner

3D Nef polyhedra, are a boundary representation for cell-complexes bounded by halfspaces that supports Boolean operations and topological operations in full generality including unbounded cells, mixed dimensional cells (e.g., isolated vertices and antennas). Nef polyhedra distinguish between open and closed sets and can represent non-manifold geometry.

Introduced in: CGAL 3.1
Depends on: 2D Boolean Operations on Nef Polygons, 2D Boolean Operations on Nef Polygons Embedded on the Sphere
BibTeX: cgal:hk-bonp3-19a
License: GPL
Windows Demo: Polyhedron demo
Common Demo Dlls: dlls

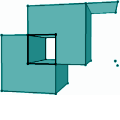
A Nef polyhedron is any point set generated from a finite number of open halfspaces by set complement and set intersection operations. In our implementation of Nef polyhedra in 3-dimensional space, we offer a B-rep data structures that is closed under boolean operations and with all their generality. Starting from halfspaces (and also directly from oriented 2-manifolds), we can work with set union, set intersection, set difference, set complement, interior, exterior, boundary, closure, and regularization operations. In essence, we can evaluate a CSG-tree with halfspaces as primitives and convert it into a B-rep representation.

In fact, we work with two data structures; one that represents the local neighborhoods of vertices, which is in itself already a complete description, and a data structure that connects these neighborhoods up to a global data structure with edges, facets, and volumes. We offer a rich interface to investigate these data structures, their different elements and their connectivity. We provide affine (rigid) tranformations and a point location query operation. We have a custom file format for storing and reading Nef polyhedra from files. We offer a simple OpenGL visualization for debugging and illustrations.

Classified Reference Pages

Classes

• CGAL::Nef_polyhedron_3<Traits>
• CGAL::Nef_polyhedron_3<Traits>::Vertex
• CGAL::Nef_polyhedron_3<Traits>::Halfedge
• CGAL::Nef_polyhedron_3<Traits>::Halffacet
• CGAL::Nef_polyhedron_3<Traits>::Volume
• CGAL::Nef_polyhedron_3<Traits>::SHalfedge
• CGAL::Nef_polyhedron_3<Traits>::SHalfloop
• CGAL::Nef_polyhedron_3<Traits>::SFace
• CGAL::Nef_polyhedron_3<Traits>::SFace_cycle_iterator

Functions

• CGAL::OFF_to_nef_3()
• CGAL::convert_nef_polyhedron_to_polygon_mesh()
• CGAL::operator<<()
• CGAL::operator>>()

Modules
	I/O Functions

Classes
class	CGAL::Nef_nary_union_3< Nef_polyhedron_3 >
	This class helps to perform the union of a set of 3D Nef polyhedra efficiently. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::Halfedge
	A Halfedge has a double meaning. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::Halffacet_cycle_iterator
	The type Halffacet_cycle_iterator iterates over a list of Object_handles. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::Halffacet
	A halffacet is an oriented, rectilinear bounded part of a plane. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::SFace_cycle_iterator
	The type SFace_cycle_iterator iterates over a list of Object_handles. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::SFace
	An sface is described by its boundaries. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::SHalfedge
	A shalfedge is a great arc on a sphere map. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::SHalfloop
	A shalfloop is a great circle on a sphere map. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::Vertex
	A vertex is a point in the 3-dimensional space. More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >::Volume
	A volume is a full-dimensional connected point set in \( \mathbb{R}^3\). More...
class	CGAL::Nef_polyhedron_3< Nef_polyhedronTraits_3, Nef_polyhedronItems_3 >
	A 3D Nef polyhedron is a subset of the 3-dimensional space that is the result of forming complements and intersections starting from a finite set H of 3-dimensional halfspaces. More...