|
CGAL 4.9.1 - Halfedge Data Structures
|
|
CGAL 4.9.1 - Halfedge Data Structures
|
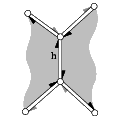
A halfedge data structure (abbreviated as HalfedgeDS, or HDS for template parameters) is an edge-centered data structure capable of maintaining incidence information of vertices, edges and faces, for example for planar maps or polyhedral surfaces. It is a combinatorial data structure, geometric interpretation is added by classes built on top of the halfedge data structure.These classes might be more convenient to use than the halfedge data structure directly, since the halfedge data structure is meant as an implementation layer.See for example the Polyhedron_3 class in the package 3D Polyhedral Surface.
The data structure provided here is known as the FE-structure [9], as halfedges [6], [2] or as the doubly connected edge list (DCEL) [3], although the original reference for the DCEL [7] describes a related but different data structure. The halfedge data structure can also be seen as one of the variants of the quad-edge data structure [4]. In general, the quad-edge data can represent non-orientable 2-manifolds, but the variant here is restricted to orientable 2-manifolds only. An overview and comparison of these different data structures together with a thorough description of the design implemented here can be found in [5].
HalfedgeDS<Traits,Items,Alloc>HalfedgeDSItemsHalfedgeDSVertexHalfedgeDSHalfedgeHalfedgeDSFaceCGAL::HalfedgeDS_default<Traits,HalfedgeDSItems,Alloc>CGAL::HalfedgeDS_list<Traits,HalfedgeDSItems,Alloc>CGAL::HalfedgeDS_vector<Traits,HalfedgeDSItems,Alloc>CGAL::HalfedgeDS_min_itemsCGAL::HalfedgeDS_items_2CGAL::HalfedgeDS_vertex_base<Refs>CGAL::HalfedgeDS_halfedge_base<Refs>CGAL::HalfedgeDS_face_base<Refs>CGAL::HalfedgeDS_vertex_min_base<Refs>CGAL::HalfedgeDS_halfedge_min_base<Refs>CGAL::HalfedgeDS_face_min_base<Refs>CGAL::HalfedgeDS_items_decorator<HDS>CGAL::HalfedgeDS_decorator<HDS>CGAL::HalfedgeDS_const_decorator<HDS> Modules | |
| Concepts | |
| Halfedge Data Structures | |
| Item Classes | |
| Vertices, Halfedges, Faces | |
| Decorators | |
| Classes that provide additional functions to examine and to modify a halfedge data structure. | |