Julia Flötotto

This package implements different methods for scattered data interpolation: Given measures of a function on a set of discrete data points, the task is to interpolate this function on an arbitrary query point. The package further offers functions for natural neighbor interpolation.

Introduced in: CGAL 3.1
BibTeX: cgal:f-i-20b
License: GPL

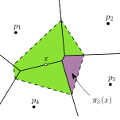
Scattered data interpolation solves the following problem: given measures of a function on a set of discrete data points, the task is to interpolate this function on an arbitrary query point.

If the function is a linear function and given barycentric coordinates that allow to express the query point as the convex combination of some data points, the function can be exactly interpolated. If the function gradients are known, we can exactly interpolate quadratic functions given barycentric coordinates. Any further properties of these interpolation functions depend on the properties of the barycentric coordinates. They are provided in this package under the names linear_interpolation() and quadratic_interpolation().

Natural Neighbor Interpolation

Natural neighbor coordinates are defined by Sibson in 1980 and are based on the Voronoi diagram of the data points. Interpolation methods based on natural neighbor coordinates are particularly interesting because they adapt easily to non-uniform and highly anisotropic data. This package contains Sibson's \( C^1\) continuous interpolation method which interpolates exactly spherical quadrics (of the form \( \Phi(\mathbf{x})= a + \mathbf{b}^t \mathbf{x} +\gamma\ \mathbf{x}^t\mathbf{x}\)) and Farin's \( C^1\) continuous interpolation method based on Bernstein-Bézier techniques and interpolating exactly quadratic functions - assuming that the function gradient is known. In addition, Sibson defines a method to approximate the function gradients for data points that are in the interior of the convex hull. This method is exact for spherical quadrics.

This CGAL package provides functions to compute the natural neighbor coordinates with respect to a two-dimensional Voronoi diagram (i. e., from the Delaunay triangulation of the data points) and to a two-dimensional power diagram for weighted points (i. e., from their regular triangulation). Natural neighbor coordinates on closed and well-sampled surfaces can also be computed if the normal to the surface at the query point is known. The latter coordinates are only approximately barycentric, see [2]. Furthermore, it implements Sibson's and Farin's interpolation functions as well as Sibson's function gradient fitting method. For a more thorough introduction, see the User Manual .

Classified Reference Pages

Concepts

Interpolation Functions

Natural Neighbor Coordinate Computation

Surface Neighbor and Surface Neighbor Coordinate Computation

Modules
	Concepts

	Interpolation Functions

	Natural Neighbor Coordinate Computation

	Surface Neighbor and Surface Neighbor Coordinate Computation

Classes
struct	CGAL::Data_access< Map >
	The struct `Data_access` implements a functor that allows to retrieve data from an associative container. More...