
 |
The classes CGAL::HalfedgeDS_items_decorator<HDS>, CGAL::HalfedgeDS_decorator<HDS>, and CGAL::HalfedgeDS_const_decorator<HDS> provide additional functions to examine and to modify a halfedge data structure HDS. The class CGAL::HalfedgeDS_items_decorator<HDS> provides additional functions for vertices, halfedges, and faces of a halfedge data structure without knowing the containing halfedge data structure. The class CGAL::HalfedgeDS_decorator<HDS> stores a reference to the halfedge data structure and provides functions that modify the halfedge data structure, for example Euler-operators. The class CGAL::HalfedgeDS_const_decorator<HDS> stores a const reference to the halfedge data structure. It contains non-modifying functions, for example the test for validness of the data structure.
All these additional functions take care of the different capabilities a halfedge data structure may have or may not have. The functions evaluate the type tags of the halfedge data structure to decide on the actions. If a particular feature is not supported nothing is done. Note that for example the creation of new halfedges is mandatory for all halfedge data structures and will not appear here again.
#include <CGAL/HalfedgeDS_decorator.h>
CGAL::HalfedgeDS_items_decorator<HDS>
|
| |
|
keeps internally a reference to hds.
| |
The following member functions do not update affected incidence relations except if mentioned otherwise.
|
|
|
removes the first vertex if vertices are supported.
| ||||
|
|
| removes the last vertex if vertices are supported. | ||||
|
|
| |||||
removes the vertex if vertices are supported.
| ||||||
|
|
| |||||
removes the range if vertices
are supported.
| ||||||
|
|
|
removes the first face if faces are supported.
| ||||
|
|
| removes the last face if faces are supported. | ||||
|
|
|
removes the face if faces are supported.
| ||||
|
|
| |||||
removes the range if faces are
supported.
| ||||||
|
|
|
removes the
face incident to h from hds and changes all halfedges
incident to the face into border edges or removes them from the
halfedge data structure if they were already border edges. If this
creates isolated vertices they get removed as well. See
make_hole(h) for a more specialized variant.
| ||||
|
|
| |||||
removes the vertices, halfedges, and faces that belong to the
connected component of .
| ||||||
|
|
|
removes the face incident to h from hds and creates a hole.
| ||||
|
|
|
fills the hole incident to h with a new face from hds.
Returns h.
| ||||
|
|
| |||||
fills the hole incident to h with a copy of face .
Returns h.
| ||||||
|
|
| |||||
extends the surface with a new face from hds into the hole
incident to and . It creates a new edge connecting the vertex
denoted by with the vertex denoted by and fills this separated
part of the hole with a new face, such that the new face is incident
to . Returns the new halfedge that is incident to the new face.
| ||||||
|
|
| |||||
extends the surface with a copy of face into the hole
incident to and . It creates a new edge connecting the tip of
with the tip of and fills this separated part of the hole with a
copy of face , such that the new face is incident to . Returns
the new halfedge that is incident to the new face.
| ||||||
The following Euler operations modify consistently the combinatorial structure of the halfedge data structure. The geometry remains unchanged. Note that well known graph operations are also captured with these Euler operators, for example an edge contraction is equal to a join_vertex() operation, or an edge removal to join_face().
Given a halfedge data structure hds and a halfedge handle four special applications of the Euler operators are worth mentioning: split_vertex(h,h) results in an antenna emanating from the tip of h; split_vertex(h,h->next()->opposite()) results in an edge split of the halfedge h->next with a new vertex in-between; split_face(h,h) results in a loop directly following h; and split_face(h,h->next()) results in a bridge parallel to the halfedge h->next with a new face in-between.
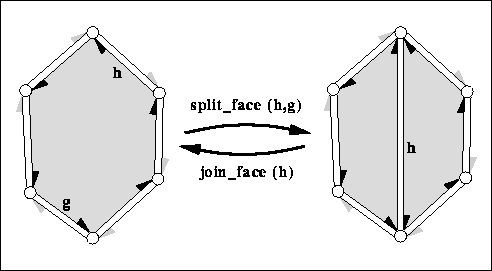
|
|
| |||
| splits the face incident to h and g into two faces with a new diagonal between the two vertices denoted by h and g respectively. The second (new) face obtained from hds is a copy of the first face. Returns h->next() after the operation, i.e., the new diagonal. The new face is to the right of the new diagonal, the old face is to the left. The time is proportional to the distance from h to g around the face. | ||||
|
|
|
joins the two faces incident to . The face incident to
h->opposite() gets removed from hds. Both faces might be
holes. Returns the predecessor of around the face. The invariant
join_face( split_face( h, g)) returns and keeps
the data structure unchanged. The time is proportional to the size
of the face removed and the time to compute h->prev().
| ||
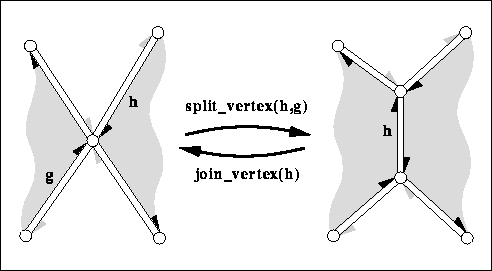
|
|
| |||
| splits the vertex incident to h and g into two vertices and connects them with a new edge. The second (new) vertex obtained from hds is a copy of the first vertex. Returns h->next()->opposite() after the operation, i.e., the new edge in the orientation towards the new vertex. The time is proportional to the distance from h to g around the vertex. | ||||
|
|
| |||
joins the two vertices incident to . The vertex denoted by
h->opposite() gets removed by hds. Returns the predecessor of
around the vertex, i.e., h->opposite()->prev(). The invariant
join_vertex( split_vertex( h, g)) returns
and keeps the polyhedron unchanged.
The time is proportional to the degree of the vertex removed and
the time to compute h->prev() and h->opposite()->prev().
| ||||
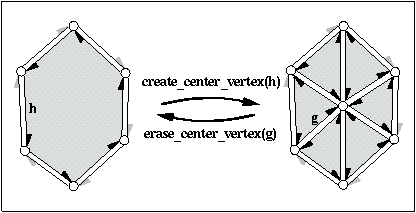
|
|
| |||||
barycentric triangulation of h->face(). Creates a new vertex,
a copy of h->vertex(), and connects it to each vertex incident
to h->face() splitting h->face() into triangles.
h remains incident to the original face, all other triangles
are copies of this face. Returns the halfedge h->next()
after the operation, i.e., a halfedge pointing to the new vertex.
The time is proportional to the size of the face.
| ||||||
|
|
| |||||
reverses create_center_vertex. Erases the
vertex pointed to by g and all incident halfedges thereby
merging all incident faces. Only g->face() remains.
The neighborhood of g->vertex() may not be triangulated,
it can have larger faces. Returns the halfedge g->prev().
Thus, the invariant h == erase_center_vertex( create_center_vertex(h)) holds if h is not a border halfedge.
The time is proportional to the sum of the size of all incident faces.
| ||||||
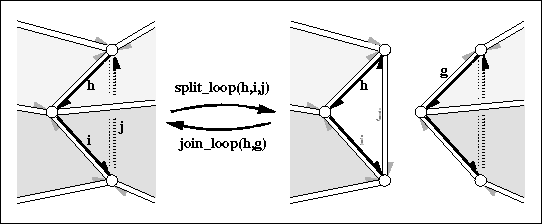
|
|
| |||||
cuts the halfedge data structure into two parts along the cycle .
Three new vertices (one copy for each vertex in the cycle) and three
new halfedges (one copy for each halfedge in the cycle), and two new
triangles are created. will be incident to the first new triangle.
The return value will be the halfedge incident to the second new triangle
which is the copy of h-opposite().
| ||||||
|
|
| |||||
glues the boundary of the two faces denoted by and together
and returns . Both faces and the vertices along the face denoted
by gets removed. Both faces may be holes. The invariant
join_loop( h, split_loop( h, i, j)) returns and keeps the
data structure unchanged.
| ||||||
These operations are the same as for CGAL::HalfedgeDS_const_decorator<HDS>.
|
|
| |
|
|
| |
|
|
|
reverses face orientations.
|
CGAL::HalfedgeDS_items_decorator<HDS>
CGAL::HalfedgeDS_const_decorator<HDS>
The following program fragment illustrates the implementation of the Euler operator split_vertex() for a simplified polyhedron class.
template <class Traits>
namespace CGAL {
class Polyhedron {
typedef HalfedgeDS_default<Traits> HDS;
HDS hds;
public:
// ...
Halfedge_handle split_vertex( Halfedge_handle h, Halfedge_handle g) {
HalfedgeDS_decorator<HDS> D(hds);
// Stricter preconditions than for HalfedgeDS only.
CGAL_precondition( D.get_vertex(h) == D.get_vertex(g));
CGAL_precondition( h != g);
return D.split_vertex( h, g);
}
};
}