|
Comparison_result
|
fo.operator() ( K::Point_3 a1, K::Point_3 b1, K::Point_3 c1, K::Point_3 d1, K::FT cosine)
|
| |
compares the dihedral angles 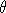 1 and 1 and 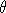 2, where 2, where
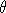 1 is the dihedral angle, in [0, π], of the tetrahedron
(a1, b1, c1, d1) at the edge (a1, b1), and 1 is the dihedral angle, in [0, π], of the tetrahedron
(a1, b1, c1, d1) at the edge (a1, b1), and 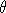 2 is
the angle in [0, π] such that cos( 2 is
the angle in [0, π] such that cos(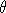 2) = cosine.
The result is the same as operator()(b1-a1, c1-a1, d1-a1, cosine). 2) = cosine.
The result is the same as operator()(b1-a1, c1-a1, d1-a1, cosine).
| Precondition: | a1, b1, c1 are not collinear,
and a1, b1, d1 are not collinear. |
|
|
|
Comparison_result
|
|
| |
compares the dihedral angles 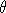 1 and 1 and 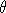 2, where 2, where
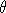 i is the dihedral angle in the tetrahedron (ai, bi,
ci, di) at the edge (ai, bi). These two angles are computed
in [0, π].
The result is the same as operator()(b1-a1, c1-a1, d1-a1, b2-a2, c2-a2, d2-a2). i is the dihedral angle in the tetrahedron (ai, bi,
ci, di) at the edge (ai, bi). These two angles are computed
in [0, π].
The result is the same as operator()(b1-a1, c1-a1, d1-a1, b2-a2, c2-a2, d2-a2).
| Precondition: | For i ∈ {1,2}, ai, bi, ci are not
collinear, and ai, bi, di are not collinear. |
|
|
|
Comparison_result
|
fo.operator() ( K::Vector_3 u1, K::Vector_3 v1, K::Vector_3 w1, K::FT cosine)
|
| |
compares the dihedral angles 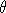 1 and 1 and 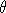 2, where 2, where
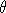 1 is the dihedral angle, in [0, π], between the
vectorial planes defined by (u1, v1) and (u1, w1), and 1 is the dihedral angle, in [0, π], between the
vectorial planes defined by (u1, v1) and (u1, w1), and
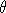 2 is the angle in [0, π] such that cos( 2 is the angle in [0, π] such that cos(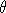 2) =
cosine. 2) =
cosine.
| Precondition: | u1 and v1 are not collinear,
and u1 and w1 are not collinear. |
|
|
|
Comparison_result
|
|
| |
compares the dihedral angles 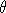 1 and 1 and 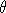 2, where 2, where
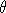 i is the dihedral angle between the vectorial planes
defined by (ui, vi) and (ui, wi). These two angles are
computed in [0, π]. i is the dihedral angle between the vectorial planes
defined by (ui, vi) and (ui, wi). These two angles are
computed in [0, π].
| Precondition: | For i ∈ {1,2}, ui and vi are not collinear,
and ui and wi are not collinear. |
|