\( \newcommand{\E}{\mathrm{E}} \) \( \newcommand{\A}{\mathrm{A}} \) \( \newcommand{\R}{\mathrm{R}} \) \( \newcommand{\N}{\mathrm{N}} \) \( \newcommand{\Q}{\mathrm{Q}} \) \( \newcommand{\Z}{\mathrm{Z}} \) \( \def\ccSum #1#2#3{ \sum_{#1}^{#2}{#3} } \def\ccProd #1#2#3{ \sum_{#1}^{#2}{#3} }\)
CGAL 4.10.1 - Point Set Processing
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Groups Pages
User Manual

Authors
Pierre Alliez, Clément Jamin, Quentin Mérigot, Jocelyn Meyron, Laurent Saboret, Nader Salman, Shihao Wu

Introduction

This CGAL component implements methods to analyze and process 3D point sets. The input is an unorganized 3D point set, possibly with normal attributes (unoriented or oriented). The input point set can be analyzed to measure geometric properties such as average spacing between the points and their k nearest neighbors. It can be processed with functions devoted to the simplification, regularization, upsampling, outlier removal, smoothing, normal estimation and normal orientation. The processing of point sets is often needed in applications dealing with measurement data, such as surface reconstruction from laser scanned data (see Figure 70.1).

introduction.jpg
Figure 70.1 Point set processing. Left: 275K points sampled on the statue of an elephant with a Minolta laser scanner. Right: point set after outlier removal, denoising and simplification to 17K points.

In the context of surface reconstruction we can position the elements of this component along the common surface reconstruction pipeline (Figure 70.2) which involves the following steps:

  1. Scanning and scan alignment to produce a set of points or points with normals (alignment is not covered in CGAL);
  2. Outlier removal;
  3. Simplification to reduce the number of input points;
  4. Smoothing to reduce noise in the input data;
  5. Normal estimation and orientation when the normals are not already provided by the acquisition device; and
  6. Surface reconstruction. Chapter Poisson Surface Reconstruction deals with surface reconstruction from point sets with normal attributes.

pipeline.jpg
Figure 70.2 Point set processing pipeline for surface reconstruction. The algorithms listed in gray are available from other CGAL components (bounding volumes and principal component analysis).

Property Maps

The algorithms of this component take as input parameters iterator ranges of 3D points, or of 3D points with normals. The property maps are used to access the point or normal information from the input data, so as to let the user decide upon the implementation of a point with normal. The latter can be represented as, e.g., a class derived from the CGAL 3D point, or as a std::pair<Point_3<K>, Vector_3<K>>, or as a boost::tuple<..,Point_3<K>, ..., Vector_3<K> >.

The following classes described in Chapter CGAL and Boost Property Maps provide property maps for the implementations of points with normals listed above:

Identity_property_map<Point_3> is the default value of the position property map expected by all functions in this component.

See below examples using pair and tuple property maps.

Users of this package may use other types to represent positions and normals if they implement the corresponding property maps.

Points and normals can even be stored in separate containers and accessed by their index, as any built-in vector is also a property map.


File Point_set_processing_3/grid_simplify_indices.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/grid_simplify_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/property_map.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
int main(int argc, char*argv[])
{
// Reads a .xyz point set file in points[].
std::vector<Point> points;
std::vector<Vector> normals;
const char* fname = (argc>1)?argv[1]:"data/fin90_with_PCA_normals.xyz";
std::ifstream stream(fname);
Point p;
Vector v;
while(stream >> p >> v){
points.push_back(p);
normals.push_back(v);
}
std::cout << points.size() << " input points" << std::endl;
std::vector<std::size_t> indices(points.size());
for(std::size_t i = 0; i < points.size(); ++i){
indices[i] = i;
}
// simplification by clustering using erase-remove idiom
double cell_size = 0.05;
std::vector<std::size_t>::iterator end;
end = CGAL::grid_simplify_point_set(indices.begin(),
indices.end(),
CGAL::make_property_map(points),
cell_size);
std::size_t k = end - indices.begin();
std::cerr << "Keep " << k << " of " << indices.size() << "indices" << std::endl;
{
std::vector<Point> tmp_points(k);
std::vector<Vector> tmp_normals(k);
for(std::size_t i=0; i<k; ++i){
tmp_points[i] = points[indices[i]];
tmp_normals[i] = normals[indices[i]];
}
points.swap(tmp_points);
normals.swap(tmp_normals);
}
std::cout << points.size() << " points after the simplification" << std::endl;
return EXIT_SUCCESS;
}

Input/Output

Streams

We provide functions to read and write sets of points or sets of points with normals from the following ASCII file formats: XYZ (three point coordinates x y z per line or three point coordinates and three normal vector coordinates x y z nx ny nz per line), OFF (Object File Format) [8] and PLY (Polygon File Format).

Note that PLY reading functions accepts binary PLY format in addition of ASCII. read_ply_custom_points() provides the user with a means to read any point property from a PLY file (for example, colors), see Example of custom PLY reader.

Example

The following example reads a point set from an input file and writes it to a file, both in the XYZ format. Positions and normals are stored in pairs and accessed through property maps.
File Point_set_processing_3/read_write_xyz_point_set_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <utility> // defines std::pair
#include <vector>
#include <fstream>
#include <iostream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored as a std::pair.
typedef std::pair<Point, Vector> Pwn;
int main(int argc, char*argv[])
{
const char* fname = (argc>1)?argv[1]:"data/oni.xyz";
// Reads a .xyz point set file in points[].
// Note: read_xyz_points_and_normals() requires an output iterator
// over points and as well as property maps to access each
// point position and normal.
std::vector<Pwn> points;
std::ifstream in(fname);
if (!in ||
!CGAL::read_xyz_points_and_normals(
in,std::back_inserter(points),
CGAL::First_of_pair_property_map<Pwn>(),
CGAL::Second_of_pair_property_map<Pwn>()))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
// Saves point set.
// Note: write_xyz_points_and_normals() requires an output iterator
// over points as well as property maps to access each
// point position and normal.
std::ofstream out("oni_copy.xyz");
if (!out ||
!CGAL::write_xyz_points_and_normals(
out, points.begin(), points.end(),
CGAL::First_of_pair_property_map<Pwn>(),
CGAL::Second_of_pair_property_map<Pwn>()))
{
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}

Example of custom PLY reader

PLY files are designed to embed an arbitrary number of additional attributes. More specifically, point sets may contain normal vectors, visibility vectors, RGB colors, intensity, etc. As it is not possible to provide dedicated functions to every possible combination of PLY properties, CGAL provides a simple way to write custom PLY readers so that the user can adapt its programs to its PLY input.

The function read_ply_custom_points() uses the concept PlyInterpreter to read specific properties defined by the user. CGAL provides, for this concept, the model CGAL::Ply_interpreter_points_and_normals_3: it is the standard interpreter that is used internally by read_ply_points() and read_ply_points_and_normals().

The following example shows how to define a custom interpreter that reads a point set with points, normals and RGB colors, and stores these attributes in user-defined containers.


File Point_set_processing_3/read_ply_points_with_colors_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_ply_points.h>
#include <utility>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored as a std::pair.
typedef std::pair<Point, Vector> Pwn;
// Color is red/green/blue array
typedef CGAL::cpp11::array<unsigned char, 3> Color;
// Custom interpreter that reads points, normals and colors and stores
// them in the appropriate container
class My_ply_interpreter
{
std::vector<Pwn>& points;
std::vector<Color>& colors;
public:
My_ply_interpreter (std::vector<Pwn>& points,
std::vector<Color>& colors)
: points (points), colors (colors)
{ }
// Init and test if input file contains the right properties
bool is_applicable (CGAL::Ply_reader& reader)
{
return reader.does_tag_exist<FT> ("x")
&& reader.does_tag_exist<FT> ("y")
&& reader.does_tag_exist<FT> ("z")
&& reader.does_tag_exist<FT> ("nx")
&& reader.does_tag_exist<FT> ("ny")
&& reader.does_tag_exist<FT> ("nz")
&& reader.does_tag_exist<unsigned char> ("red")
&& reader.does_tag_exist<unsigned char> ("green")
&& reader.does_tag_exist<unsigned char> ("blue");
}
// Describes how to process one line (= one point object)
void process_line (CGAL::Ply_reader& reader)
{
FT x = (FT)0., y = (FT)0., z = (FT)0.,
nx = (FT)0., ny = (FT)0., nz = (FT)0.;
Color c = {{ 0, 0, 0 }};
reader.assign (x, "x");
reader.assign (y, "y");
reader.assign (z, "z");
reader.assign (nx, "nx");
reader.assign (ny, "ny");
reader.assign (nz, "nz");
reader.assign (c[0], "red");
reader.assign (c[1], "green");
reader.assign (c[2], "blue");
points.push_back (std::make_pair (Point (x, y, z), Vector (nx, ny, nz)));
colors.push_back (c);
}
};
int main(int argc, char*argv[])
{
const char* fname = (argc>1) ? argv[1] : "data/colors.ply";
// Reads a .ply point set file with normal vectors and colors
std::vector<Pwn> points; // store points with normals
std::vector<Color> colors; // store colors in separate container
My_ply_interpreter interpreter(points, colors); // init interpreter
std::ifstream in(fname);
if (!in ||
!CGAL::read_ply_custom_points (in, interpreter, Kernel()))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
// Display points with pure r/g/b colors
for (std::size_t i = 0; i < points.size (); ++ i)
if (colors[i][0] == 255 && colors[i][1] == 0 && colors[i][2] == 0)
std::cerr << "Point " << points[i].first << " is red." << std::endl;
else if (colors[i][0] == 0 && colors[i][1] == 255 && colors[i][2] == 0)
std::cerr << "Point " << points[i].first << " is green." << std::endl;
else if (colors[i][0] == 0 && colors[i][1] == 0 && colors[i][2] == 255)
std::cerr << "Point " << points[i].first << " is blue." << std::endl;
return EXIT_SUCCESS;
}

Average Spacing

Function compute_average_spacing() computes the average spacing of all input points to their k nearest neighbor points, k being specified by the user. As it provides an order of a point set density, this function is used downstream the surface reconstruction pipeline to automatically determine some parameters such as output mesh sizing for surface reconstruction.

Example

The following example reads a point set in the xyz format and computes the average spacing. Index, position and color are stored in a tuple and accessed through property maps.
File Point_set_processing_3/average_spacing_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/compute_average_spacing.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
#include <boost/tuple/tuple.hpp>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_3 Point;
// Data type := index, followed by the point, followed by three integers that
// define the Red Green Blue color of the point.
typedef boost::tuple<int, Point, int, int, int> IndexedPointWithColorTuple;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(int argc, char*argv[])
{
const char* fname = (argc>1)?argv[1]:"data/sphere_20k.xyz";
// Reads a .xyz point set file in points.
// As the point is the second element of the tuple (that is with index 1)
// we use a property map that accesses the 1st element of the tuple.
std::vector<IndexedPointWithColorTuple> points;
std::ifstream stream(fname);
if (!stream ||
!CGAL::read_xyz_points(
stream, std::back_inserter(points),
CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>()))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
// Initialize index and RGB color fields in tuple.
// As the index and RGB color are respectively the first and third-fifth elements
// of the tuple we use a get function from the property map that accesses the 0
// and 2-4th elements of the tuple.
for(unsigned int i = 0; i < points.size(); i++)
{
points[i].get<0>() = i; // set index value of tuple to i
points[i].get<2>() = 0; // set RGB color to black
points[i].get<3>() = 0;
points[i].get<4>() = 0;
}
// Computes average spacing.
const unsigned int nb_neighbors = 6; // 1 ring
FT average_spacing = CGAL::compute_average_spacing<Concurrency_tag>(
points.begin(), points.end(),
CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>(),
nb_neighbors);
std::cout << "Average spacing: " << average_spacing << std::endl;
return EXIT_SUCCESS;
}

Note that other functions such as centroid or bounding volumes are found in other CGAL components:

Automatic Scale Estimation

Point sets are often used to sample objects with a higher dimension, typically a curve in 2D or a surface in 3D. In such cases, finding the scale of the objet is crucial, that is to say finding the minimal number of points (or the minimal local range) such that the subset of points has the appearance of a curve in 2D or a surface in 3D [1].

CGAL provides 2 functions that automatically estimate the scale of a 2D point set sampling a curve or a 3D point set sampling a surface:

Functions such as jet_estimate_normals() or remove_outliers() require a K neighbor scale while others such as grid_simplify_point_set() require a range scale. vcm_estimate_normals() is an example of a function that accepts both.

In some specific cases, the scale of a point set might not be homogeneous (for example if the point set contains variable noise). CGAL also provides 2 functions that automatically estimate the scales of a point set at a set of user-defined query points:

The 4 functions presented here work both with 2D points and 3D points and they shouldn't be used if the point sets do not sample a curve in 2D or a surface in 3D.

Global Scale Example

The following example reads a 3D point set in the xyz format and:

  • Estimates the K neighbor global scale
  • Uses it to smooth the point set
  • Estimates the range global scale
  • Uses it to simplify the point set


File Point_set_processing_3/scale_estimation_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/estimate_scale.h>
#include <CGAL/jet_smooth_point_set.h>
#include <CGAL/grid_simplify_point_set.h>
#include <CGAL/Timer.h>
#include <CGAL/Memory_sizer.h>
#include <vector>
#include <fstream>
#include <boost/tuple/tuple.hpp>
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_3 Point_3;
int main (int argc, char** argv)
{
const char* fname = (argc>1)?argv[1]:"data/sphere_20k.xyz";
CGAL::Timer task_timer;
std::vector<Point_3> points;
std::ifstream stream(fname);
// read input
if (!(stream
&& CGAL::read_xyz_points(stream, std::back_inserter(points))))
{
std::cerr << "Error: can't read input file" << std::endl;
return EXIT_FAILURE;
}
// estimate k scale
task_timer.start();
std::size_t k_scale = CGAL::estimate_global_k_neighbor_scale (points.begin(), points.end());
task_timer.stop();
// Example: use estimated k as scale for jet smoothing
CGAL::jet_smooth_point_set<Concurrency_tag>
(points.begin(), points.end(),
static_cast<unsigned int>(k_scale));
// estimate range scale
task_timer.start();
FT range_scale = CGAL::estimate_global_range_scale (points.begin(), points.end());
task_timer.stop();
// Example: use estimated range for grid simplification
points.erase (CGAL::grid_simplify_point_set (points.begin(), points.end(), range_scale),
points.end());
// print some informations on runtime
std::size_t memory = CGAL::Memory_sizer().virtual_size();
double time = task_timer.time();
std::cout << "Scales computed in " << time << " second(s) using "
<< (memory>>20) << " MiB of memory:" << std::endl;
std::cout << " * Global K scale: " << k_scale << std::endl;
std::cout << " * Global range scale: " << range_scale << std::endl;
return EXIT_SUCCESS;
}

Local Scales Example

This second example generates a 2D point set sampling a circle with variable noise. It then estimates the scale at 3 different query points in the domain.


File Point_set_processing_3/scale_estimation_2d_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/estimate_scale.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/Random.h>
#include <vector>
#include <fstream>
#include <boost/tuple/tuple.hpp>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_2 Point_2;
int main (int, char**)
{
std::vector<Point_2> samples;
samples.reserve (100000);
// Generate circle with gradually variable noise
// - noise-free for points with x close to (-1)
// - noisy for points with x close to (+1)
for (std::size_t i = 0; i < 100000; ++ i)
{
FT theta = CGAL::get_default_random().get_double(0, 2. * CGAL_PI);
FT noise = 0.5 * (std::cos(theta) + 1.) * CGAL::get_default_random().get_double(0., 0.2);
int mult = (CGAL::get_default_random().get_bool() ? 1 : -1);
samples.push_back (Point_2 (std::cos(theta) * (1. + mult * noise * noise),
std::sin(theta) * (1. + mult * noise * noise)));
}
// Search for local scales on 3 different locations
std::vector<Point_2> queries;
queries.reserve (3);
queries.push_back (Point_2 (-1., 0.));
queries.push_back (Point_2 (0., 1.));
queries.push_back (Point_2 (1., 0.));
std::vector<std::size_t> k_scales;
CGAL::estimate_local_k_neighbor_scales (samples.begin(), samples.end(),
queries.begin(), queries.end(),
std::back_inserter (k_scales));
// Display results
std::cerr << "K-Scales found:" << std::endl
<< " - On noise-free region: " << k_scales[0] << std::endl // Should be small
<< " - On moderately noisy region: " << k_scales[1] << std::endl // Should be higher
<< " - On very noisy region: " << k_scales[2] << std::endl; // Should be even higher
return EXIT_SUCCESS;
}

Outlier Removal

Function remove_outliers() deletes a user-specified fraction of outliers from an input point set. More specifically, it sorts the input points in increasing order of average squared distances to their k nearest neighbors and deletes the points with largest value.

Example

The following example reads a point set and removes 5% of the points. It uses the Identity_property_map<Point_3> property map (optional as it is the default position property map of all functions in this component.)
File Point_set_processing_3/remove_outliers_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/compute_average_spacing.h>
#include <CGAL/remove_outliers.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
#include <iostream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(int argc, char*argv[])
{
const char* fname = (argc>1)?argv[1]:"data/oni.xyz";
// Reads a .xyz point set file in points[].
// The Identity_property_map property map can be omitted here as it is the default value.
std::vector<Point> points;
std::ifstream stream(fname);
if (!stream ||
!CGAL::read_xyz_points(stream, std::back_inserter(points),
CGAL::Identity_property_map<Point>()))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
// Removes outliers using erase-remove idiom.
// The Identity_property_map property map can be omitted here as it is the default value.
const int nb_neighbors = 24; // considers 24 nearest neighbor points
// Estimate scale of the point set with average spacing
const double average_spacing = CGAL::compute_average_spacing<CGAL::Sequential_tag>
(points.begin(), points.end(), nb_neighbors);
// FIRST OPTION //
// I don't know the ratio of outliers present in the point set
std::vector<Point>::iterator first_to_remove
= CGAL::remove_outliers(points.begin(), points.end(),
CGAL::Identity_property_map<Point>(),
nb_neighbors,
100., // No limit on the number of outliers to remove
2. * average_spacing); // Point with distance above 2*average_spacing are considered outliers
std::cerr << (100. * std::distance(first_to_remove, points.end()) / (double)(points.size()))
<< "% of the points are considered outliers when using a distance threshold of "
<< 2. * average_spacing << std::endl;
// SECOND OPTION //
// I know the ratio of outliers present in the point set
const double removed_percentage = 5.0; // percentage of points to remove
points.erase(CGAL::remove_outliers(points.begin(), points.end(),
CGAL::Identity_property_map<Point>(),
nb_neighbors,
removed_percentage, // Minimum percentage to remove
0.), // No distance threshold (can be omitted)
points.end());
// Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
std::vector<Point>(points).swap(points);
return EXIT_SUCCESS;
}

Simplification

Four simplification functions are devised to reduce an input point set.

Function random_simplify_point_set() randomly deletes a user-specified fraction of points from the input point set. This algorithm is fast.

Function grid_simplify_point_set() considers a regular grid covering the bounding box of the input point set, and clusters all points sharing the same cell of the grid by picking as representant one arbitrarily chosen point. This algorithm is slower than random_simplify_point_set().

Function hierarchy_simplify_point_set() provides an adaptive simplification of the point set through local clusters [7]. The size of the clusters is either directly selected by the user or it automatically adapts to the local variation of the point set.

Function wlop_simplify_and_regularize_point_set() not only simplifies, but also regularizes downsampled points. This is an implementation of the Weighted Locally Optimal Projection (WLOP) algorithm [3].

Grid Simplification Example

The following example reads a point set and simplifies it by clustering.
File Point_set_processing_3/grid_simplification_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/grid_simplify_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(int argc, char*argv[])
{
// Reads a .xyz point set file in points[].
std::vector<Point> points;
const char* fname = (argc>1)?argv[1]:"data/oni.xyz";
std::ifstream stream(fname);
if (!stream ||
!CGAL::read_xyz_points(stream, std::back_inserter(points)))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
// simplification by clustering using erase-remove idiom
double cell_size = 0.001;
points.erase(CGAL::grid_simplify_point_set(points.begin(), points.end(), cell_size),
points.end());
// Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
std::vector<Point>(points).swap(points);
return EXIT_SUCCESS;
}

grid_simplification.jpg
Figure 70.3 Point set simplification through grid-based clustering. Removed points are depicted in red. Notice how low-density areas (in green) are not simplified.

Hierarchy Simplification Example

The following example reads a point set and produces a set of clusters.


File Point_set_processing_3/hierarchy_simplification_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/hierarchy_simplify_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <CGAL/Timer.h>
#include <CGAL/Memory_sizer.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
int main(int argc, char*argv[])
{
// Reads a .xyz point set file in points[].
std::vector<Point> points;
const char* fname = (argc>1)?argv[1]:"data/oni.xyz";
std::ifstream stream(fname);
if (!stream ||
!CGAL::read_xyz_points(stream, std::back_inserter(points)))
{
std::cerr << "Error: cannot read file " << fname << std::endl;
return EXIT_FAILURE;
}
std::cout << "Read " << points.size () << " point(s)" << std::endl;
CGAL::Timer task_timer; task_timer.start();
// simplification by clustering using erase-remove idiom
points.erase (CGAL::hierarchy_simplify_point_set (points.begin (), points.end (),
100, // Max cluster size
0.01), // Max surface variation
points.end ());
std::size_t memory = CGAL::Memory_sizer().virtual_size();
std::cout << points.size () << " point(s) kept, computed in "
<< task_timer.time() << " seconds, "
<< (memory>>20) << " Mib allocated." << std::endl;
std::ofstream f ("out.xyz");
CGAL::write_xyz_points (f, points.begin (), points.end ());
return EXIT_SUCCESS;
}

Parameter: size

The hierarchy simplification algorithm recursively split the point set in two until each cluster's size is less than the parameter size.

hierarchical_clustering_size.jpg
Figure 70.4 Input point set and hierarchy simplification with different size parameter: \(10\), \(100\) and \(1000\). In the 3 cases, var_max \(=1/3\).

Parameter: var_max

In addition to the size parameter, a variation parameter allows to increase simplification in monotoneous regions. For each cluster, a surface variation measure is computed using the sorted eigenvalues of the covariance matrix:

\[ \sigma(p) = \frac{\lambda_0}{\lambda_0 + \lambda_1 + \lambda_2}. \]

This function goes from \(0\) if the cluster is coplanar to \(1/3\) if it is fully isotropic. If a cluster's variation is above var_max, it is split. If var_max is equal to \(1/3\), this parameter has no effect and the clustering is regular on the whole point set.

hierarchical_clustering_var_max.jpg
Figure 70.5 Input point set and hierarchy simplification with different var_max parameter: \(0.00001\), \(0.001\) and \(0.1\). In the 3 cases, size \(=1000\).

WLOP Simplification Example

The following example reads a point set, simplifies and regularizes it by WLOP.


File Point_set_processing_3/wlop_simplify_and_regularize_point_set_example.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/wlop_simplify_and_regularize_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <vector>
#include <fstream>
#include <iostream>
// types
typedef CGAL::Simple_cartesian<double> Kernel;
typedef Kernel::Point_3 Point;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(int argc, char** argv)
{
const char* input_filename = (argc>1)?argv[1]:"data/sphere_20k.xyz";
const char* output_filename = (argc>2)?argv[2]:"data/sphere_20k_WLOPED.xyz";
// Reads a .xyz point set file in points[]
std::vector<Point> points;
std::ifstream stream(input_filename);
if (!stream || !CGAL::read_xyz_points(stream, std::back_inserter(points)))
{
std::cerr << "Error: cannot read file " << input_filename << std::endl;
return EXIT_FAILURE;
}
std::vector<Point> output;
//parameters
const double retain_percentage = 2; // percentage of points to retain.
const double neighbor_radius = 0.5; // neighbors size.
CGAL::wlop_simplify_and_regularize_point_set
<Concurrency_tag>
(points.begin(),
points.end(),
std::back_inserter(output),
retain_percentage,
neighbor_radius
);
std::ofstream out(output_filename);
if (!out || !CGAL::write_xyz_points(
out, output.begin(), output.end()))
{
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}

simplification_comparison.jpg
Figure 70.6 Comparison for three simplification methods: Left: Random simplification result. Middle: Grid simplification result. Right: WLOP simplification result.

Parameter: require_uniform_sampling

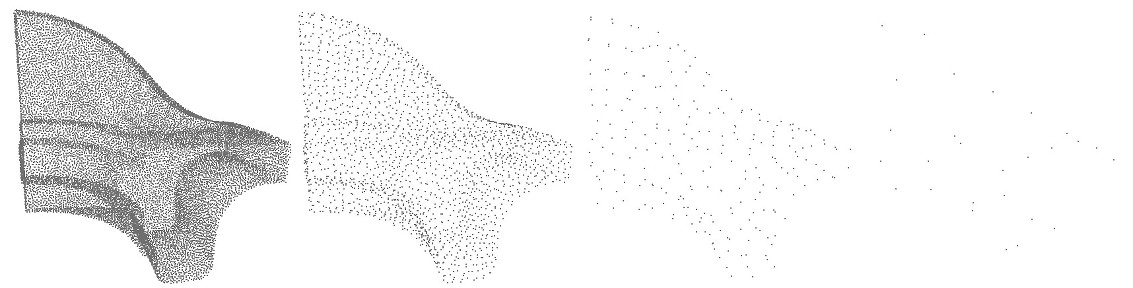
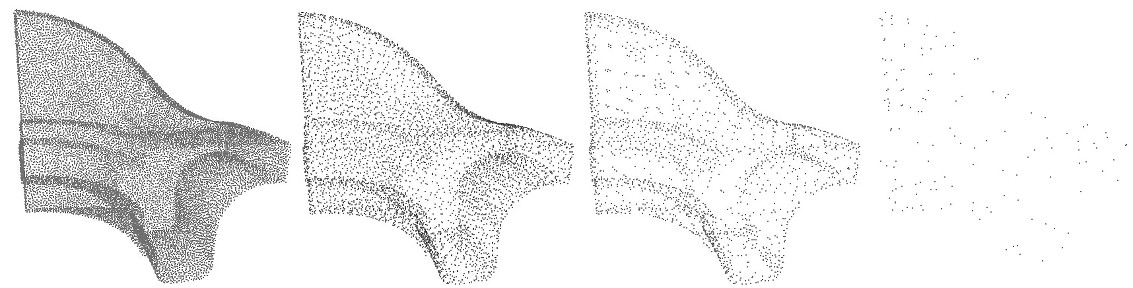
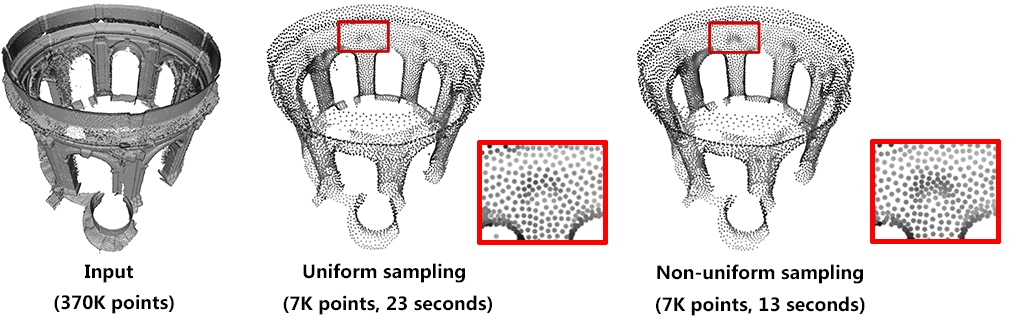
Computing density weights for each point is an optional preprocessing. For example, as shown in the following figure, when require_uniform_sampling is set to false, WLOP preserves the intrinsic non-uniform sampling of the original points; if require_uniform_sampling is set to true, WLOP is resilient to non-uniform sampling and generates sample points with more uniform distribution, at the expense of computational time.

WLOP_parameter_density.jpg
Figure 70.7 Comparison between with and without density: Left: input. Middle: require_uniform_sampling = false. Right: require_uniform_sampling=true.

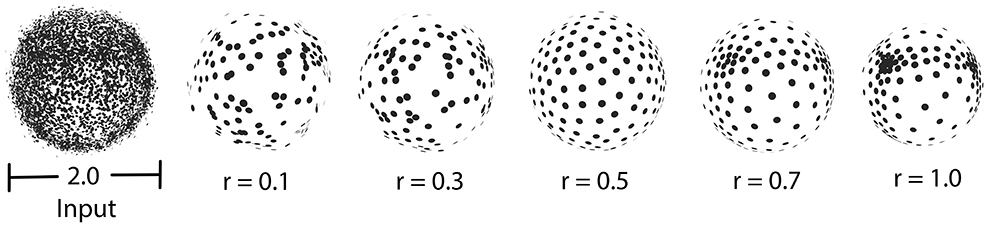
Parameter: neighbor_radius

Usually, the neighborhood of sample points should include at least two rings of neighboring sample points. Using a small neighborhood size may not be able to generate regularized result, while using big neighborhood size will make the sample points shrink into the interior of the local surface (under-fitting). The function will use a neighborhood size estimation if this parameter value is set to default or smaller that zero.

WLOP_parameter_neighborhood_size.jpg
Figure 70.8 Comparison between different sizes of neighbor radius.

Parallel Performance

A parallel version of WLOP is provided and requires the executable to be linked against the Intel TBB library. To control the number of threads used, the user may use the tbb::task_scheduler_init class. See the TBB documentation for more details. We provide below a speed-up chart generated using the parallel version of the WLOP algorithm. The machine used is a PC running Windows 7 64-bits with a 4-core i7-47.nosp@m.00HQ.nosp@m.@2.40.nosp@m.GHz CPU with 8GB of RAM.

parallel_WLOP_performance.jpg
Figure 70.9 Parallel WLOP speed-up, compared to the sequential version of the algorithm.

Smoothing

Two smoothing functions are devised to smooth an input point set.

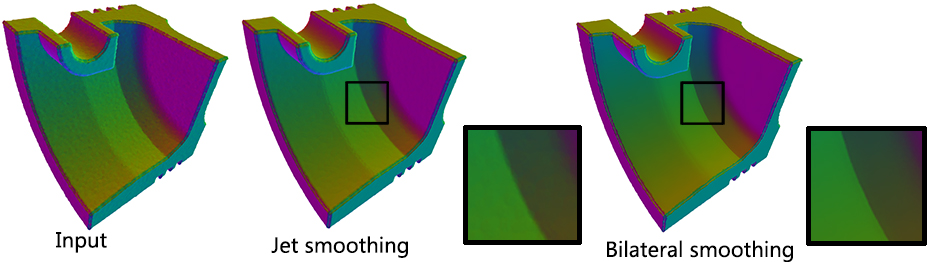
Function jet_smooth_point_set() smooths the input point set by projecting each point onto a smooth parametric surface patch (so-called jet surface) fitted over its k nearest neighbors.

Function bilateral_smooth_point_set() smooths the input point set by iteratively projecting each point onto the implicit surface patch fitted over its k nearest neighbors. Bilateral projection preserves sharp features according to the normal (gradient) information. Normals are thus required as input. For more details, see section 4 of [4].

Jet Smoothing Example

The following example generates a set of 9 points close to the xy plane and smooths them using 8 nearest neighbors:
File Point_set_processing_3/jet_smoothing_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/jet_smooth_point_set.h>
#include <vector>
// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(void)
{
// generate point set
std::vector<Point> points;
points.push_back(Point( 0.0, 0.0, 0.001));
points.push_back(Point(-0.1,-0.1, 0.002));
points.push_back(Point(-0.1,-0.2, 0.001));
points.push_back(Point(-0.1, 0.1, 0.002));
points.push_back(Point( 0.1,-0.1, 0.000));
points.push_back(Point( 0.1, 0.2, 0.001));
points.push_back(Point( 0.2, 0.0, 0.002));
points.push_back(Point( 0.2, 0.1, 0.000));
points.push_back(Point( 0.0,-0.1, 0.001));
// Smoothing.
const unsigned int nb_neighbors = 8; // default is 24 for real-life point sets
CGAL::jet_smooth_point_set<Concurrency_tag>(points.begin(), points.end(), nb_neighbors);
return EXIT_SUCCESS;
}

Bilateral Smoothing Example

The following example reads a set of points with normals and smooths them via bilateral smoothing:
File Point_set_processing_3/bilateral_smooth_point_set_example.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <CGAL/bilateral_smooth_point_set.h>
#include <CGAL/tags.h>
#include <utility> // defines std::pair
#include <fstream>
// Types
typedef CGAL::Simple_cartesian<double> Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(int argc, char*argv[])
{
const char* input_filename = (argc>1)?argv[1]:"data/fin90_with_PCA_normals.xyz";
const char* output_filename = (argc>2)?argv[2]:"data/fin90_with_PCA_normals_bilateral_smoothed.xyz";
// Reads a .xyz point set file in points[] * with normals *.
std::vector<PointVectorPair> points;
std::ifstream stream(input_filename);
if (!stream ||
!CGAL::read_xyz_points_and_normals(stream,
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>()))
{
std::cerr << "Error: cannot read file " << input_filename << std::endl;
return EXIT_FAILURE;
}
// Algorithm parameters
int k = 120; // size of neighborhood. The bigger the smoother the result will be.
// This value should bigger than 1.
double sharpness_angle = 25; // control sharpness of the result.
// The bigger the smoother the result will be
int iter_number = 3; // number of times the projection is applied
for (int i = 0; i < iter_number; ++i)
{
/* double error = */
CGAL::bilateral_smooth_point_set <Concurrency_tag>(
points.begin(),
points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
k,
sharpness_angle);
}
std::ofstream out(output_filename);
if (!out ||
!CGAL::write_xyz_points_and_normals(
out, points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>()))
{
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}

smoothing_comparison.jpg
Figure 70.10 Comparison for two smoothing methods: Left: Input, 250K points, normal-color mapping. Middle: Jet smoothing result, 197 seconds. Right: Bilateral smoothing result, 110 seconds.

Parallel

Performance: A parallel version of bilateral smoothing is provided and requires the executable to be linked against the Intel TBB library. The number of threads used is controlled through the tbb::task_scheduler_init class. See the TBB documentation for more details. We provide below a speed-up chart generated using the parallel version of the bilateral smoothing algorithm. The machine used is a PC running Windows 7 64-bits with a 4-core i7-47.nosp@m.00HQ.nosp@m.@2.40.nosp@m.GHz CPU with 8GB of RAM.

parallel_bilateral_smooth_point_set_performance.jpg
Figure 70.11 Parallel bilateral smoothing speed-up, compared to the sequential version of the algorithm.

Normal Estimation

Assuming a point set sampled over an inferred surface S, two functions provide an estimate of the normal to S at each point. The result is an unoriented normal vector for each input point.

Function jet_estimate_normals() estimates the normal direction at each point from the input set by fitting a jet surface over its k nearest neighbors. The default jet is a quadric surface. This algorithm is well suited to point sets scattered over curved surfaces.

Function pca_estimate_normals() estimates the normal direction at each point from the set by linear least squares fitting of a plane over its k nearest neighbors. This algorithm is simpler and faster than jet_estimate_normals().

Function vcm_estimate_normals() estimates the normal direction at each point from the set by using the Voronoi Covariance Measure of the point set. This algorithm is more complex and slower than the previous algorithms. It is based on the article [6].

Normal Orientation

Function mst_orient_normals() orients the normals of a set of points with unoriented normals using the method described by Hoppe et al. in Surface reconstruction from unorganized points [2]. More specifically, this method constructs a Riemannian graph over the input points (the graph of the k nearest neighbor points) and propagates a seed normal orientation within a minimum spanning tree computed over this graph. The result is an oriented normal vector for each input unoriented normal, except for the normals which cannot be successfully oriented.

mst_orient_normals.jpg
Figure 70.12 Normal orientation of a sampled cube surface. Left: unoriented normals. Right: orientation of right face normals is propagated to bottom face.

Example

The following example reads a point set from a file, estimates the normals through PCA over the 6 nearest neighbors and orients the normals:
File Point_set_processing_3/normals_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/pca_estimate_normals.h>
#include <CGAL/mst_orient_normals.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <utility> // defines std::pair
#include <list>
#include <fstream>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(int argc, char*argv[])
{
const char* fname = (argc>1)?argv[1]:"data/sphere_1k.xyz";
// Reads a .xyz point set file in points[].
std::list<PointVectorPair> points;
std::ifstream stream(fname);
if (!stream ||
!CGAL::read_xyz_points(stream,
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>()))
{
std::cerr << "Error: cannot read file " << fname<< std::endl;
return EXIT_FAILURE;
}
// Estimates normals direction.
// Note: pca_estimate_normals() requires an iterator over points
// as well as property maps to access each point's position and normal.
const int nb_neighbors = 18; // K-nearest neighbors = 3 rings
CGAL::pca_estimate_normals<Concurrency_tag>(points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
nb_neighbors);
// Orients normals.
// Note: mst_orient_normals() requires an iterator over points
// as well as property maps to access each point's position and normal.
std::list<PointVectorPair>::iterator unoriented_points_begin =
CGAL::mst_orient_normals(points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
nb_neighbors);
// Optional: delete points with an unoriented normal
// if you plan to call a reconstruction algorithm that expects oriented normals.
points.erase(unoriented_points_begin, points.end());
return EXIT_SUCCESS;
}

Upsampling

The function edge_aware_upsample_point_set() generates a denser point set from an input point set. This has applications in point-based rendering, hole filling, and sparse surface reconstruction. The algorithm can progressively upsample the point set while approaching the edge singularities. See [4] for more details.

Example

The following example reads a point set from a file, upsamples it to get a denser result.


File Point_set_processing_3/edge_aware_upsample_point_set_example.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/edge_aware_upsample_point_set.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <vector>
#include <fstream>
// types
typedef CGAL::Simple_cartesian<double> Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;
// Concurrency
#ifdef CGAL_LINKED_WITH_TBB
typedef CGAL::Parallel_tag Concurrency_tag;
#else
typedef CGAL::Sequential_tag Concurrency_tag;
#endif
int main(int argc, char* argv[])
{
const char* input_filename = (argc>1)?argv[1]:"data/before_upsample.xyz";
const char* output_filename = (argc>2)?argv[2]:"data/before_upsample_UPSAMPLED.xyz";
// Reads a .xyz point set file in points[], *with normals*.
std::vector<PointVectorPair> points;
std::ifstream stream(input_filename);
if (!stream ||
!CGAL::read_xyz_points_and_normals(stream,
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>()))
{
std::cerr << "Error: cannot read file " << input_filename << std::endl;
return EXIT_FAILURE;
}
//Algorithm parameters
const double sharpness_angle = 25; // control sharpness of the result.
const double edge_sensitivity = 0; // higher values will sample more points near the edges
const double neighbor_radius = 0.25; // initial size of neighborhood.
const std::size_t number_of_output_points = points.size() * 4;
//Run algorithm
CGAL::edge_aware_upsample_point_set<Concurrency_tag>(
points.begin(),
points.end(),
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>(),
sharpness_angle,
edge_sensitivity,
neighbor_radius,
number_of_output_points);
// Saves point set.
std::ofstream out(output_filename);
if (!out ||
!CGAL::write_xyz_points_and_normals(
out, points.begin(), points.end(),
CGAL::First_of_pair_property_map<PointVectorPair>(),
CGAL::Second_of_pair_property_map<PointVectorPair>()))
{
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}

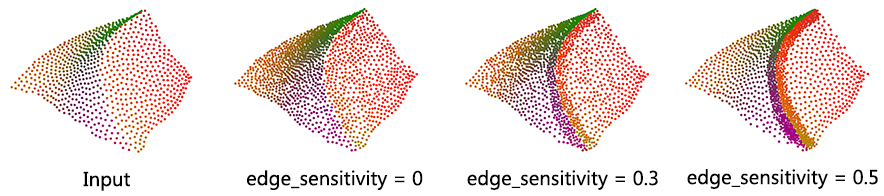
Parameter: edge_sensitivity

This parameter controls where the new points are inserted. Larger values of edge-sensitivity give higher priority to inserting points along the sharp features. For example, as shown in the following figure, high value is preferable when one wants to insert more points on sharp features, where the local gradient is high, e.g., darts, cusps, creases and corners. In contrast, points are evenly inserted when edge_sensitivity is set to 0. The range of possible value is [0, 1].

upsample_edge_sensitivity.jpg
Figure 70.13 Upsampling for different edge-sensitivity parameter values. The input containing 850 points is upsampled to 1,500 points in all cases depicted.

Parameter: sharpness_angle

This parameter controls the preservation of sharp features.

upsample_sharpness_angle.jpg
Figure 70.14 Upsampling for different sharpness_angle parameter values. The input containing 850 points is upsampled to 425K points in all cases depicted.

Parameter: neighbor_radius

Usually, the neighborhood of sample points should include at least one ring of neighboring sample points. Using small neighborhood size may not be able to insert new points. Using big neighborhood size can fill small holes, but points inserted on the edges could be irregular. The function will use a neigbhorhood size estimation if this parameter value is set to default or smaller than zero.

upsample_neighborhood_size.jpg
Figure 70.15 Comparison between different sizes of neighbor radius.

Feature Edges Estimation

Function vcm_is_on_feature_edge() indicates if a points belong to a feature edges of the point set using its Voronoi Covariance Measure. It is based on the article [6].

It first computes the VCM of the points set using compute_vcm(). Then, it estimates which points belong to a sharp edge by testing if a ratio of eigenvalues is greater than a given threshold.

Example

The following example reads a point set from a file, estimates the points that are on sharp edges:
File Point_set_processing_3/edges_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/vcm_estimate_edges.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_off_points.h>
#include <utility> // defines std::pair
#include <vector>
#include <fstream>
#include <boost/foreach.hpp>
// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;
// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;
typedef std::vector<PointVectorPair> PointList;
typedef CGAL::cpp11::array<double,6> Covariance;
int main (int , char**) {
// Reads a .xyz point set file in points[].
std::list<PointVectorPair> points;
std::ifstream stream("data/fandisk.off");
if (!stream ||
!CGAL::read_off_points(stream,
std::back_inserter(points),
CGAL::First_of_pair_property_map<PointVectorPair>()))
{
std::cerr << "Error: cannot read file data/fandisk.off" << std::endl;
return EXIT_FAILURE;
}
// Estimates covariance matrices per points.
double R = 0.2,
r = 0.1;
std::vector<Covariance> cov;
CGAL::First_of_pair_property_map<PointVectorPair> point_pmap;
CGAL::compute_vcm(points.begin(), points.end(), point_pmap, cov, R, r, Kernel());
// Find the points on the edges.
// Note that this step is not expensive and can be done several time to get better results
double threshold = 0.16;
std::ofstream output("points_on_edges.xyz");
int i = 0;
BOOST_FOREACH(const PointVectorPair& p, points)
{
if (CGAL::vcm_is_on_feature_edge(cov[i], threshold))
output << p.first << "\n";
++i;
}
return 0;
}

Structuring

The function structure_point_set() generates a structured version of the input point set. It requires that a shape detection algorithm is first applied to the point set (see Chapter_Point_Set_Shape_Detection). It is based on the article [5].

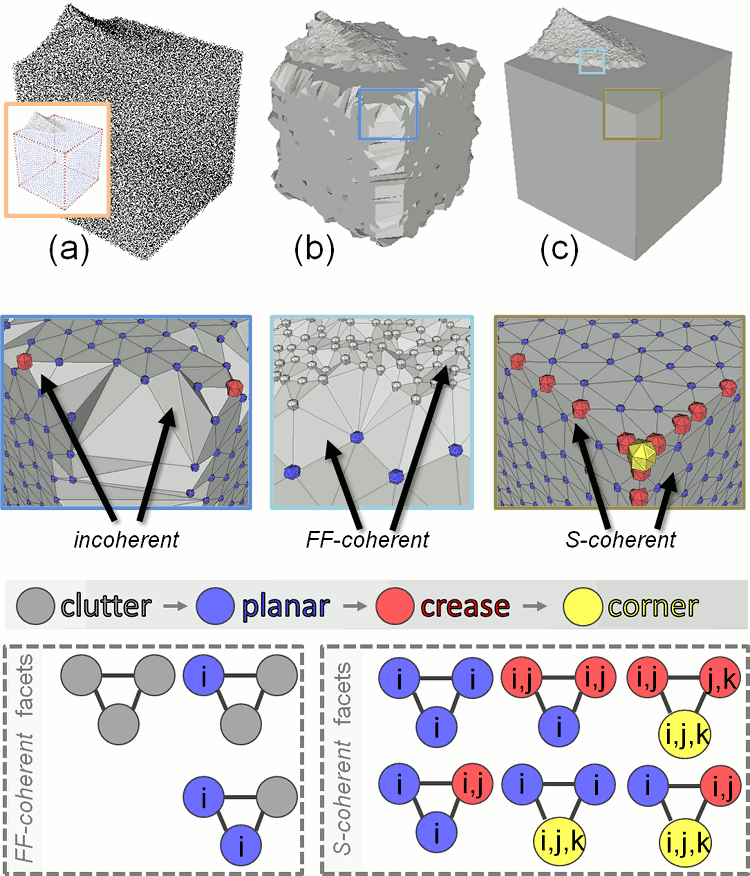
  • Planes: inliers of each detected plane are replaced by sets of noise-free points sampled at the vertices of a regular grid: this is achieved by filling an occupancy grid aligned on the principal components of the inlier sets with a spacing lower than \(\sqrt{2}\) times the user-defined tolerance.
  • Creases: adjacencies between 2 planes are detected and regularly resampled on an occupancy array along the edge with a spacing equal to twice the user-defined tolerance.
  • Corners: 3-cycles are detected from the primitive adjacency graph and sampled using the exact intersection point of the 3 planes (provided it exists and remains in the given tolerance). These corners are also locally clustered to former corners of degree higher than 3.

This algorithm is well suited to point sets sampled on surfaces with planar sections and sharp edges.

structuring.png
Figure 70.17 Point set structuring. Left: input raw point set. Right: structured point set.

Structure information of points can be used to perform feature preserving reconstruction (see Advancing Front Surface Reconstruction for example). More specifically, the class storing a point set with structure provides the user with a method Point_set_with_structure::facet_coherence() that estimates if a triplet of points form a coherent facet.

structuring_coherence.png
Figure 70.17 (a) Input point set (and structured output); (b) output with many incoherent facets; (c) output with all facets coherent. i, j and k each corresponds to a primitive index.

Example

The following example applies shape detection followed by structuring to a point set:
File Point_set_processing_3/structuring_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>
#include <CGAL/Point_with_normal_3.h>
#include <CGAL/property_map.h>
#include <CGAL/Shape_detection_3.h>
#include <CGAL/structure_point_set.h>
#include <iostream>
#include <fstream>
// Type declarations
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef std::pair<Kernel::Point_3, Kernel::Vector_3> Point_with_normal;
typedef std::vector<Point_with_normal> Pwn_vector;
typedef CGAL::First_of_pair_property_map<Point_with_normal> Point_map;
typedef CGAL::Second_of_pair_property_map<Point_with_normal> Normal_map;
// Efficient RANSAC types
typedef CGAL::Shape_detection_3::Efficient_RANSAC_traits
<Kernel, Pwn_vector, Point_map, Normal_map> Traits;
typedef CGAL::Shape_detection_3::Efficient_RANSAC<Traits> Efficient_ransac;
typedef CGAL::Shape_detection_3::Plane<Traits> Plane;
int main (int argc, char** argv)
{
// Points with normals.
Pwn_vector points;
// Loading point set from a file.
std::ifstream stream(argc>1 ? argv[1] : "data/cube.pwn");
if (!stream ||
!CGAL::read_xyz_points_and_normals(stream,
std::back_inserter(points),
Point_map(),
Normal_map()))
{
std::cerr << "Error: cannot read file cube.pwn" << std::endl;
return EXIT_FAILURE;
}
std::cerr << points.size() << " point(s) read." << std::endl;
// Shape detection
Efficient_ransac ransac;
ransac.set_input(points);
ransac.add_shape_factory<Plane>();
ransac.detect();
Pwn_vector structured_pts;
CGAL::structure_point_set (points.begin (), points.end (), // input points
std::back_inserter (structured_pts),
ransac, // shape detection engine
0.015); // epsilon for structuring points
std::cerr << structured_pts.size ()
<< " structured point(s) generated." << std::endl;
std::ofstream out ("out.pwn");
CGAL::write_xyz_points_and_normals (out, structured_pts.begin(), structured_pts.end(),
Point_map(), Normal_map());
out.close();
return EXIT_SUCCESS;
}

Implementation History

Pierre Alliez and Laurent Saboret contributed the initial component. Nader Salman contributed the grid simplification. Started from GSoC'2013, three new algorithms were implemented by Shihao Wu and Clément Jamin: WLOP, bilateral smoothing and upsampling. Started from GSoC'2014, Jocelyn Meyron with the help of Quentin Mérigot introduced the computation of the Voronoi covarience measure of a point set, as well as the normal and feature edge estimation functions based on it.