|
CGAL 4.10.2 - 2D Periodic Triangulations
|
|
CGAL 4.10.2 - 2D Periodic Triangulations
|
#include <CGAL/Periodic_2_triangulation_2.h>
Inherited by CGAL::Periodic_2_Delaunay_triangulation_2< Traits, Tds >.
The class Periodic_2_triangulation_2 represents a 2-dimensional triangulation of a point set in \( \mathbb T_c^2\).
Parameters
The class Periodic_2_triangulation_2 has two template parameters. The first one
| Traits | is the geometric traits, it is to be instantiated by a model of the concept Periodic_2TriangulationTraits_2. |
The second parameter
| TDS | is the triangulation data structure, it has to be instantiated by a model of the concept TriangulationDataStructure_2 with some additional functionality in faces. By default, the triangulation data structure is instantiated by CGAL::Triangulation_data_structure_2 < CGAL::Triangulation_vertex_base_2<Gt>, CGAL::Periodic_2_triangulation_face_base_2<Gt> > >. |
Traversal of the Triangulation
The periodic triangulation class provides several iterators and circulators that allow one to traverse it.
I/O
The I/O operators are defined for iostream. The format for the iostream is an internal format.
The information in the iostream is:
number_of_sheets()Implementation
Locate is implemented by a randomized walk from a vertex of the face given as optional parameter (or from an arbitrary vertex of if no optional parameter is given).
Insertion of a point is done by locating a face that contains the point, and then splitting this face. Apart from the location, insertion takes a time \( O(1)\).
Removal of a vertex is more difficult than in the Euclidean space, since the star of a vertex may not be disjoint from the star of a virtual copy of that vertex. Therefore generic removal of vertices is not implemented. Several more constrained cases are implemented: the removal of the last vertex in the triangulation and the removal of a vertex of degree 3.
The face, edge, and vertex iterators on features are derived from their counterparts visiting all (non-virtual and virtual) features which are themselves derived from the corresponding iterators of the triangulation data structure.
Public Types | |
| enum | Iterator_type { STORED = 0, UNIQUE, STORED_COVER_DOMAIN, UNIQUE_COVER_DOMAIN } |
The enum Iterator_type is defined by Periodic_2_triangulation_2 to specify the behavior of geometric iterators. More... | |
| enum | Locate_type { VERTEX = 0, EDGE, FACE, EMPTY } |
The enum @ is defined by Periodic_2_triangulation_2 to specify which case occurs when locating a point in the triangulation. More... | |
Related Functions | |
(Note that these are not member functions.) | |
| ostream & | operator<< (ostream &os, const Periodic_2_triangulation_2< Traits, Tds > &t) |
Writes the triangulation t into the stream os. More... | |
| istream & | operator>> (istream &is, Triangulation_2< Traits, Tds > &t) |
Reads a triangulation from stream is and assigns it to t. More... | |
Types | |
| typedef Traits | Geom_traits |
| the traits class. | |
| typedef Tds | Triangulation_data_structure |
| the triangulation data structure type. | |
|
typedef Geom_traits::Periodic_2_offset_2 | Offset |
| the offset type. | |
|
typedef Geom_traits::Iso_rectangle_2 | Iso_rectangle |
| the iso rectangle type. | |
| typedef array< int, 2 > | Covering_sheets |
| integer tuple to store the number of sheets in each direction of space. | |
| typedef Geom_traits::Point_2 | Point |
| the point type. | |
| typedef Geom_traits::Segment_2 | Segment |
| the segment type. | |
| typedef Geom_traits::Triangle_2 | Triangle |
| the triangle type. | |
| typedef std::pair< Point, Offset > | Periodic_point |
| represents a point-offset pair. More... | |
| typedef array< Periodic_point, 2 > | Periodic_segment |
| a pair of periodic points representing a segment in the periodic domain. | |
| typedef array< Periodic_point, 3 > | Periodic_triangle |
| a triple of periodic points representing a triangle in the periodic domain. | |
| typedef Tds::Vertex | Vertex |
| the vertex type. | |
| typedef Tds::Face | Face |
| the face type. | |
| typedef Tds::Edge | Edge |
| the edge type. | |
| typedef Tds::size_type | size_type |
| size type (an unsigned integral type). | |
| typedef Tds::difference_type | difference_type |
| difference type (a signed integral type). | |
Handles, Iterators and Circulators | |
The vertices and faces of the triangulations are accessed through The handles are
The edges of the triangulation can also be visited through iterators and circulators, the edge circulators and iterators are also bidirectional and non-mutable. | |
| typedef Tds::Vertex_handle | Vertex_handle |
| handle to a vertex. | |
| typedef Tds::Face_handle | Face_handle |
| handle to a face. | |
| typedef Tds::Face_iterator | Face_iterator |
| iterator over all faces. | |
| typedef Tds::Edge_iterator | Edge_iterator |
| iterator over all edges. | |
| typedef Tds::Vertex_iterator | Vertex_iterator |
| iterator over all vertices. | |
| typedef unspecified_type | Unique_vertex_iterator |
| iterator over the vertices whose corresponding points lie in the original domain, i.e. More... | |
| typedef Face_iterator | Finite_faces_iterator |
| typedef Edge_iterator | Finite_edges_iterator |
| typedef Vertex_iterator | Finite_vertices_iterator |
| typedef Face_iterator | All_faces_iterator |
| typedef unspecified_type | Face_circulator |
| circulator over all faces incident to a given vertex. | |
| typedef unspecified_type | Edge_circulator |
| circulator over all edges incident to a given vertex. | |
| typedef unspecified_type | Vertex_circulator |
| circulator over all vertices adjacent to a given vertex. | |
Geometric iterators: | |
| typedef unspecified_type | Periodic_triangle_iterator |
| iterator over the triangles corresponding to faces of the triangulation. | |
| typedef unspecified_type | Periodic_segment_iterator |
| iterator over the segments corresponding to edges of the triangulation. | |
| typedef unspecified_type | Periodic_point_iterator |
| iterator over the points corresponding to vertices of the triangulation. | |
Creation | |
| Triangulation_2 (const Iso_rectangle &domain=Iso_rectangle(0, 0, 1, 1), const Geom_traits &traits=Geom_traits()) | |
Introduces an empty triangulation t with domain as original domain. More... | |
| Triangulation_2 (const Triangulation_2 &tr) | |
| Copy constructor. More... | |
| Triangulation_2 | operator= (const Triangulation_2< Traits, Tds > &tr) |
| Assignment. More... | |
| void | swap (Triangulation_2 &tr) |
The triangulations tr and this are swapped. More... | |
| void | clear () |
| Deletes all faces and vertices resulting in an empty triangulation. | |
Access Functions | |
The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of the | |
| const Geom_traits & | geom_traits () const |
| Returns a const reference to the triangulation traits object. | |
|
const Triangulation_data_structure_2 & | tds () const |
| Returns a const reference to the triangulation data structure. | |
| Iso_rectangle | domain () const |
| Returns the original domain. | |
| Covering_sheets | number_of_sheets () const |
| Returns the number of sheets of the covering space the triangulation is currently computed in. | |
| int | dimension () const |
| Returns the dimension of the convex hull. More... | |
| size_type | number_of_vertices () const |
| Returns the number of vertices. More... | |
| size_type | number_of_faces () const |
| Returns the number of faces. More... | |
| size_type | number_of_stored_vertices () const |
| Returns the number of vertices in the data structure. More... | |
| size_type | number_of_stored_faces () const |
| Returns the number of faces in the data structure. More... | |
Non const access | |
Advanced This method is mainly a help for users implementing their own triangulation algorithms. | |
| Triangulation_data_structure_2 & | tds () |
Non-constant-time access functions | |
| size_type | number_of_edges () const |
| Returns the number of edges. More... | |
| size_type | number_of_stored_edges () const |
| Returns the number of edges in the data structure. More... | |
Non-constant-time queries and conversions | |
Advanced It is not recommended to interfere with the built-in covering management. Especially a premature conversion to the 1-sheeted covering space might lead to problems when modifying the triangulation later. | |
| bool | is_extensible_triangulation_in_1_sheet_h1 () const |
| Advanced The current triangulation remains a triangulation in the 1-sheeted covering space even after adding points if this method returns true. More... | |
| bool | is_extensible_triangulation_in_1_sheet_h2 () const |
| Advanced The same as is_extensible_triangulation_in_1_sheet_h1() but with a more precise heuristic, i.e. More... | |
| bool | is_triangulation_in_1_sheet () const |
| Advanced Returns true if the current triangulation would still be a triangulation in the 1-sheeted covering space, returns false otherwise. More... | |
| void | convert_to_1_sheeted_covering () |
| Advanced Converts the current triangulation into the same periodic triangulation in the 1-sheeted covering space. More... | |
| void | convert_to_9_sheeted_covering () |
| Advanced Converts the current triangulation into the same periodic triangulation in the 9-sheeted covering space. More... | |
Geometric access functions | |
| Periodic_point | periodic_point (const Vertex_handle v) const |
Returns the periodic point given by vertex v. More... | |
| Periodic_point | periodic_point (const Face_handle f, int i) const |
If this is represented in the 1-sheeted covering space, this function returns the periodic point given by the \( i\)-th vertex of face f, that is the point in the original domain and the offset of the vertex in f. More... | |
| Periodic_segment | periodic_segment (const Face_handle f, int i) const |
Returns the periodic segment formed by the two point-offset pairs corresponding to the two vertices of edge (f,i). More... | |
| Periodic_segment | periodic_segment (const Edge &e) const |
Same as the previous method for edge e. | |
| Periodic_triangle | periodic_triangle (const Face_handle f) const |
Returns the periodic triangle formed by the three point-offset pairs corresponding to the three vertices of facet f. | |
Note that a traits class providing exact constructions should be used in order to guarantee the following operations to be exact (as opposed to computing the triangulation only, which requires only exact predicates). | |
| Point | point (const Periodic_point &pp) const |
Converts the Periodic_point pp (point-offset pair) to the corresponding Point in \( \mathbb R^3\). | |
| Segment | segment (const Periodic_segment &s) const |
Converts the Periodic_segment s to a Segment. | |
| Triangle | triangle (const Periodic_triangle &t) const |
Converts the Periodic_triangle this to a Triangle. | |
| Point | circumcenter (Face_handle f) const |
| Compute the circumcenter of the face pointed to by f. More... | |
| Segment | segment (Face_handle f, int i) const |
Equivalent to the call t.segment(t.periodic_segment(f,i)); | |
| Segment | segment (const Edge &e) const |
Equivalent to the call t.segment(t.periodic_segment(e)); | |
| Segment | segment (const Edge_circulator &ec) const |
Equivalent to the call t.segment(t.periodic_segment(ec->first, ec->second)); | |
| Segment | segment (const Edge_iterator &ei) const |
Equivalent to the call t.segment(t.periodic_segment(ei->first, ei->second)); | |
| Triangle | triangle (Face_handle f) const |
Equivalent to the call t.triangle(t.periodic_triangle(f)); | |
Predicates | |
The class | |
| bool | is_edge (Vertex_handle va, Vertex_handle vb) |
true if there is an edge having va and vb as vertices. | |
| bool | is_edge (Vertex_handle va, Vertex_handle vb, Face_handle &fr, int &i) |
| as above. More... | |
| bool | is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3) |
true if there is a face having v1, v2 and v3 as vertices. | |
| bool | is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3, Face_handle &fr) |
| as above. More... | |
Queries | |
The class It also provides methods to locate a point with respect to a given face of the triangulation. | |
| Face_handle | locate (const Point &query, Face_handle f=Face_handle()) const |
| If the triangulation is not empty, a face that contains the query in its interior or on its boundary is returned. More... | |
| Face_handle | locate (const Point &query, Locate_type <, int &li, Face_handle h=Face_handle()) const |
| Same as above. More... | |
| Oriented_side | oriented_side (Face_handle f, const Point &p) const |
Returns on which side of the oriented boundary of f the point p lies. | |
| Oriented_side | side_of_oriented_circle (Face_handle f, const Point &p) |
Returns on which side of the circumcircle of face f lies the point p. More... | |
Face, Edge and Vertex Iterators | |
The following iterators allow the user to visit faces, edges and vertices of the stored triangulation, i.e. in case of computing in a multiply sheeted covering space all stored periodic copies of each item are returned. These iterators are non-mutable, bidirectional and their value types are respectively | |
| Vertex_iterator | vertices_begin () const |
| Starts at an arbitrary vertex. | |
| Vertex_iterator | vertices_end () const |
| Past-the-end iterator. | |
| Edge_iterator | edges_begin () const |
| Starts at an arbitrary edge. | |
| Edge_iterator | edges_end () const |
| Past-the-end iterator. | |
| Face_iterator | faces_begin () const |
| Starts at an arbitrary face. | |
| Face_iterator | faces_end () const |
| Past-the-end iterator. | |
Geometric iterators | |
The following iterators allow the user to obtain geometric primitives corresponding to faces, edges, and vertices of the triangulation. These iterators are non-mutable, bidirectional and their value types are respectively 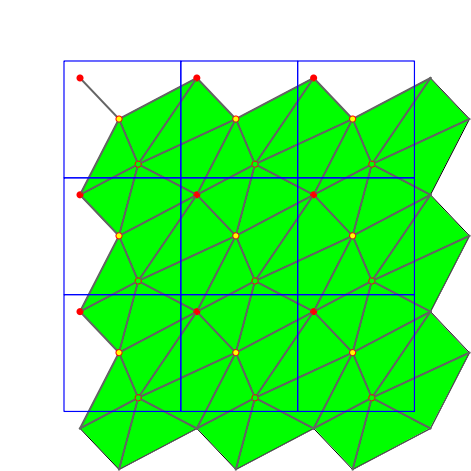
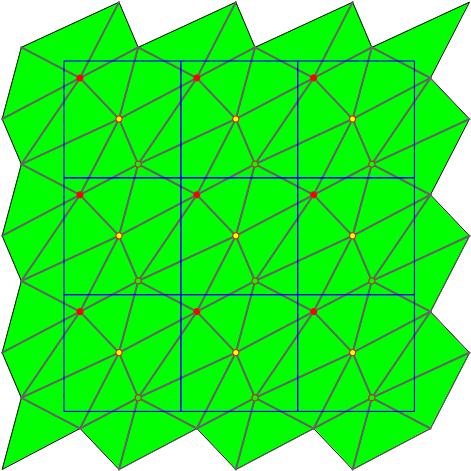
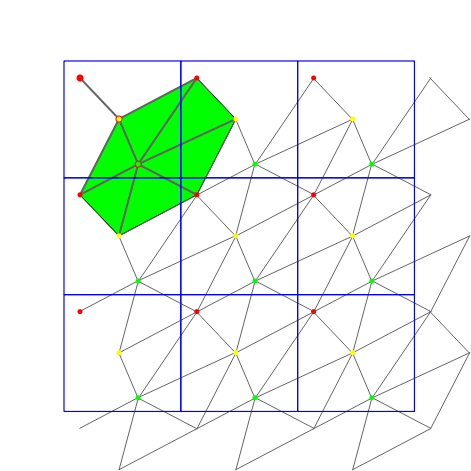
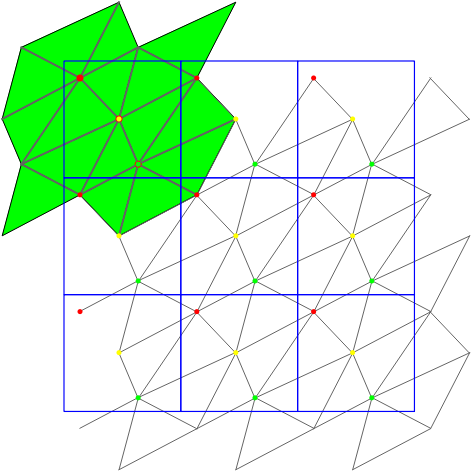
STORED, STORED_COVER_DOMAIN, UNIQUE, UNIQUE_COVER_DOMAIN. Note that in case of computing in the 1-sheeted covering space, stored and unique give the same result. | |
| Periodic_point_iterator | periodic_points_begin (Iterator_type it=STORED) const |
| Iterates over the points of the triangulation. More... | |
| Periodic_point_iterator | periodic_points_end (Iterator_type it=STORED) const |
| Past-the-end iterator. More... | |
| Periodic_segment_iterator | periodic_segments_begin (Iterator_type it=STORED) const |
| Iterates over the segments of the triangulation. More... | |
| Periodic_segment_iterator | periodic_segments_end (Iterator_type it=STORED) const |
| Past-the-end iterator. More... | |
| Periodic_triangle_iterator | periodic_triangles_begin (Iterator_type it=STORED) const |
| Iterates over the triangles of the triangulation. More... | |
| Periodic_triangle_iterator | periodic_triangles_end (Iterator_type it=STORED) const |
| Past-the-end iterator. More... | |
Face, Edge and Vertex Circulators | |
The triangulation also provides circulators that allows to visit respectively all faces or edges incident to a given vertex or all vertices adjacent to a given vertex. These circulators are non-mutable and bidirectional. The | |
| Face_circulator | incident_faces (Vertex_handle v) const |
Starts at an arbitrary face incident to v. | |
| Face_circulator | incident_faces (Vertex_handle v, Face_handle f) const |
Starts at face f. More... | |
| Edge_circulator | incident_edges (Vertex_handle v) const |
Starts at an arbitrary edge incident to v. | |
| Edge_circulator | incident_edges (Vertex_handle v, Face_handle f) const |
Starts at the first edge of f incident to v, in counterclockwise order around v. More... | |
| Vertex_circulator | adjacent_vertices (Vertex_handle v) const |
Starts at an arbitrary vertex adjacent to v. | |
| Vertex_circulator | adjacent_vertices (Vertex_handle v, Face_handle f) |
Starts at the first vertex of f adjacent to v in counterclockwise order around v. More... | |
Traversal between adjacent faces | |
| Vertex_handle | mirror_vertex (Face_handle f, int i) const |
returns the vertex of the \( i^{th}\) neighbor of f that is opposite to f. More... | |
| int | mirror_index (Face_handle f, int i) const |
returns the index of f in its \( i^{th}\) neighbor. More... | |
| Vertex_handle | insert (const Point &p, Face_handle f=Face_handle()) |
| Vertex_handle | insert (const Point &p, Locate_type lt, Face_handle loc, int li) |
| Vertex_handle | push_back (const Point &p) |
| template<class InputIterator > | |
| int | insert (InputIterator first, InputIterator last) |
Advanced The following member functions offer more specialized versions of the insertion or removal operations to be used when one knows to be in the corresponding case. 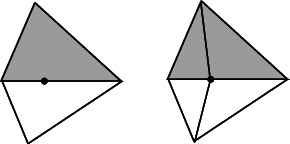
Insertion of a point on an edge. 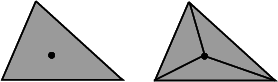
Insertion in a face. The following functions are mainly intended to be used in conjunction with the | |
| Vertex_handle | insert_first (const Point &p) |
| Vertex_handle | insert_in_face (const Point &p, Face_handle f) |
| void | remove_degree_3 (Vertex_handle v) |
| void | remove_first (Vertex_handle v) |
| template<class EdgeIt > | |
| Vertex_handle | star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end) |
| Advanced creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end]. More... | |
| template<class EdgeIt , class FaceIt > | |
| Vertex_handle | star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end, FaceIt face_begin, FaceIt face_end) |
| Advanced same as above, except that the algorithm first recycles faces in the sequence [face_begin, face_end] and create new ones only when the sequence is exhausted. More... | |
| void | set_domain (const Iso_rectangle dom) |
Miscellaneous | |
| int | ccw (int i) const |
| Returns \( i+1\) modulo 3. More... | |
| int | cw (int i) const |
| Returns \( i+2\) modulo 3. More... | |
| void | flippable (Face_handle f, int i) |
| size_t | degree (Vertex_handle v) |
Returns the degree of the vertex v | |
Checking | |
Advanced The responsibility of keeping a valid triangulation belongs to the users if advanced operations are used. Obviously the advanced user, who implements higher levels operations may have to make a triangulation invalid at some times. The following method is provided to help the debugging. | |
| bool | is_valid (bool verbose=false, int level=0) const |
| Advanced Checks the combinatorial validity of the triangulation and also the validity of its geometric embedding. More... | |
| typedef std::pair< Point, Offset > CGAL::Periodic_2_triangulation_2< Traits, Tds >::Periodic_point |
represents a point-offset pair.
The point in the pair lies in the original domain.
| typedef unspecified_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::Unique_vertex_iterator |
iterator over the vertices whose corresponding points lie in the original domain, i.e.
for each set of periodic copies the Unique_vertex_iterator iterates over exactly one representative.
| enum CGAL::Periodic_2_triangulation_2::Iterator_type |
The enum Iterator_type is defined by Periodic_2_triangulation_2 to specify the behavior of geometric iterators.
| Enumerator | |
|---|---|
| STORED |
Return all geometric primitives as they are stored internally in |
| UNIQUE |
Return only one representative of each geometric primitive even if the triangulation is computed in a multiply sheeted covering space. Choose the representative whose maximum offset is minimal but non-negative in each direction of space. |
| STORED_COVER_DOMAIN |
Same as |
| UNIQUE_COVER_DOMAIN |
Same as |
| enum CGAL::Periodic_2_triangulation_2::Locate_type |
The enum @ is defined by Periodic_2_triangulation_2 to specify which case occurs when locating a point in the triangulation.
If the triangulation does not contain any points EMPTY is returned.
| Vertex_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::adjacent_vertices | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) |
Starts at the first vertex of f adjacent to v in counterclockwise order around v.
f is incident to vertex v. | int CGAL::Periodic_2_triangulation_2< Traits, Tds >::ccw | ( | int | i) | const |
Returns \( i+1\) modulo 3.
| Point CGAL::Periodic_2_triangulation_2< Traits, Tds >::circumcenter | ( | Face_handle | f) | const |
Compute the circumcenter of the face pointed to by f.
This function is available only if the corresponding function is provided in the geometric traits.
| void CGAL::Periodic_2_triangulation_2< Traits, Tds >::convert_to_1_sheeted_covering | ( | ) |
is_triangulation_in_1_sheet() | void CGAL::Periodic_2_triangulation_2< Traits, Tds >::convert_to_9_sheeted_covering | ( | ) |
| int CGAL::Periodic_2_triangulation_2< Traits, Tds >::cw | ( | int | i) | const |
Returns \( i+2\) modulo 3.
| int CGAL::Periodic_2_triangulation_2< Traits, Tds >::dimension | ( | ) | const |
Returns the dimension of the convex hull.
The dimension is zero if the triangulation is empty and two otherwise.
| Edge_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::incident_edges | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) | const |
Starts at the first edge of f incident to v, in counterclockwise order around v.
f is incident to vertex v. | Face_circulator CGAL::Periodic_2_triangulation_2< Traits, Tds >::incident_faces | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) | const |
Starts at face f.
f is incident to vertex v. | Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::insert_first | ( | const Point & | p) |
| Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::insert_in_face | ( | const Point & | p, |
| Face_handle | f | ||
| ) |
v in face f.
Face f is modified, two new faces are created. If the triangulation contains periodic copies, a point is inserted in all periodic copies.
v lies inside face f. | bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_edge | ( | Vertex_handle | va, |
| Vertex_handle | vb, | ||
| Face_handle & | fr, | ||
| int & | i | ||
| ) |
as above.
In addition, if true is returned, the edge with vertices va and vb is the edge e=(fr,i) where fr is a handle to the face incident to e and on the right side of e oriented from va to vb.
| bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_extensible_triangulation_in_1_sheet_h1 | ( | ) | const |
true.
This test relies on a heuristic, i.e. if it answers false nothing is known. This test runs in constant-time when not computing in the 1-sheeted covering space. (This test uses the length of the longest edge in the triangulation as a criterion [1].)
| bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_extensible_triangulation_in_1_sheet_h2 | ( | ) | const |
is_extensible_triangulation_in_1_sheet_h1() but with a more precise heuristic, i.e.
it might answer true in cases in which is_extensible_triangulation_in_1_sheet_h1() would not. However, it is much less time efficient when not computing in the 1-sheeted covering space. (This test uses the diameter of the largest empty circle in the input point set as a criterion [1].)
| bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_face | ( | Vertex_handle | v1, |
| Vertex_handle | v2, | ||
| Vertex_handle | v3, | ||
| Face_handle & | fr | ||
| ) |
as above.
In addition, if true is returned, fr is a handle to the face with v1, v2 and v3 as vertices.
| bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_triangulation_in_1_sheet | ( | ) | const |
true if the current triangulation would still be a triangulation in the 1-sheeted covering space, returns false otherwise.
| bool CGAL::Periodic_2_triangulation_2< Traits, Tds >::is_valid | ( | bool | verbose = false, |
| int | level = 0 |
||
| ) | const |
This method is mainly a debugging help for the users of advanced features.
| Face_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::locate | ( | const Point & | query, |
| Face_handle | f = Face_handle() |
||
| ) | const |
If the triangulation is not empty, a face that contains the query in its interior or on its boundary is returned.
If the triangulation is empty, the default constructed Face_handle is returned.
| Face_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::locate | ( | const Point & | query, |
| Locate_type & | lt, | ||
| int & | li, | ||
| Face_handle | h = Face_handle() |
||
| ) | const |
Same as above.
Additionally, the parameters lt and li describe where the query point is located. The variable lt is set to the locate type of the query. If lt==VERTEX the variable li is set to the index of the vertex, and if lt==EDGE li is set to the index of the vertex opposite to the edge. Be careful that li has no meaning when the query type is FACE or when the triangulation is \( 0\)-dimensional.
| int CGAL::Periodic_2_triangulation_2< Traits, Tds >::mirror_index | ( | Face_handle | f, |
| int | i | ||
| ) | const |
returns the index of f in its \( i^{th}\) neighbor.
| Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::mirror_vertex | ( | Face_handle | f, |
| int | i | ||
| ) | const |
returns the vertex of the \( i^{th}\) neighbor of f that is opposite to f.
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_edges | ( | ) | const |
Returns the number of edges.
Counts all edges that are representatives of the same segment in \( \mathbb T_c^2\) as one edge.
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_faces | ( | ) | const |
Returns the number of faces.
Counts all faces that are representatives of the same triangle in \( \mathbb T_c^2\) as one face.
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_edges | ( | ) | const |
Returns the number of edges in the data structure.
This is the same as the number of sheets times number_of_edges().
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_faces | ( | ) | const |
Returns the number of faces in the data structure.
This is the same as the number of sheets times number_of_faces().
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_stored_vertices | ( | ) | const |
Returns the number of vertices in the data structure.
This is the same as the number of sheets times number_of_vertices().
| size_type CGAL::Periodic_2_triangulation_2< Traits, Tds >::number_of_vertices | ( | ) | const |
Returns the number of vertices.
Counts all vertices that are representatives of the same point in \( \mathbb T_c^2\) as one vertex.
| Triangulation_2 CGAL::Periodic_2_triangulation_2< Traits, Tds >::operator= | ( | const Triangulation_2< Traits, Tds > & | tr) |
Assignment.
All the vertices and faces are duplicated. After the assignment, this and tr refer to different triangulations: if tr is modified, this is not.
| Periodic_point CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_point | ( | const Vertex_handle | v) | const |
Returns the periodic point given by vertex v.
If this is represented in the 1-sheeted covering space, the offset is always zero. Otherwise v can correspond to a periodic copy outside the domain of an input point.
| Periodic_point CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_point | ( | const Face_handle | f, |
| int | i | ||
| ) | const |
If this is represented in the 1-sheeted covering space, this function returns the periodic point given by the \( i\)-th vertex of face f, that is the point in the original domain and the offset of the vertex in f.
If this is represented in the 9-sheeted covering space, this offset is possibly added to another offset determining the periodic copy.
| Periodic_point_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_points_begin | ( | Iterator_type | it = STORED) | const |
Iterates over the points of the triangulation.
Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.
| Periodic_point_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_points_end | ( | Iterator_type | it = STORED) | const |
Past-the-end iterator.
Note that to match another Periodic_point_iterator both must have the same Iterator_type it.
| Periodic_segment CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segment | ( | const Face_handle | f, |
| int | i | ||
| ) | const |
Returns the periodic segment formed by the two point-offset pairs corresponding to the two vertices of edge (f,i).
| Periodic_segment_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segments_begin | ( | Iterator_type | it = STORED) | const |
Iterates over the segments of the triangulation.
Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.
| Periodic_segment_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_segments_end | ( | Iterator_type | it = STORED) | const |
Past-the-end iterator.
Note that to match another Periodic_segment_iterator both must have the same Iterator_type it.
| Periodic_triangle_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_triangles_begin | ( | Iterator_type | it = STORED) | const |
Iterates over the triangles of the triangulation.
Its behavior is defined by the Iterator_type it as described on CGAL::Periodic_2_triangulation_2::Iterator_type.
| Periodic_triangle_iterator CGAL::Periodic_2_triangulation_2< Traits, Tds >::periodic_triangles_end | ( | Iterator_type | it = STORED) | const |
Past-the-end iterator.
Note that to match another Periodic_triangle_iterator both must have the same Iterator_type it.
| void CGAL::Periodic_2_triangulation_2< Traits, Tds >::remove_degree_3 | ( | Vertex_handle | v) |
Two of the incident faces are destroyed, the third one is modified.
v is a vertex with degree three. | void CGAL::Periodic_2_triangulation_2< Traits, Tds >::remove_first | ( | Vertex_handle | v) |
| void CGAL::Periodic_2_triangulation_2< Traits, Tds >::set_domain | ( | const Iso_rectangle | dom) |
Note that this function calls clear(), i.e., it erases the existing triangulation.
| Oriented_side CGAL::Periodic_2_triangulation_2< Traits, Tds >::side_of_oriented_circle | ( | Face_handle | f, |
| const Point & | p | ||
| ) |
Returns on which side of the circumcircle of face f lies the point p.
The circle is assumed to be counterclockwise oriented, so its positive side correspond to its bounded side. This predicate is available only if the corresponding predicates on points is provided in the geometric traits class.
| Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::star_hole | ( | Point | p, |
| EdgeIt | edge_begin, | ||
| EdgeIt | edge_end | ||
| ) |
v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end].
Returns a handle to the new vertex.
| Vertex_handle CGAL::Periodic_2_triangulation_2< Traits, Tds >::star_hole | ( | Point | p, |
| EdgeIt | edge_begin, | ||
| EdgeIt | edge_end, | ||
| FaceIt | face_begin, | ||
| FaceIt | face_end | ||
| ) |
[face_begin, face_end] and create new ones only when the sequence is exhausted.
| void CGAL::Periodic_2_triangulation_2< Traits, Tds >::swap | ( | Triangulation_2 & | tr) |
The triangulations tr and this are swapped.
t.swap(tr) should be preferred to this = tr or to t(tr) if tr is deleted after that.
| Triangulation_data_structure_2& CGAL::Periodic_2_triangulation_2< Traits, Tds >::tds | ( | ) |
| CGAL::Periodic_2_triangulation_2< Traits, Tds >::Triangulation_2 | ( | const Iso_rectangle & | domain = Iso_rectangle(0, 0, 1, 1), |
| const Geom_traits & | traits = Geom_traits() |
||
| ) |
Introduces an empty triangulation t with domain as original domain.
domain is a square. | CGAL::Periodic_2_triangulation_2< Traits, Tds >::Triangulation_2 | ( | const Triangulation_2 & | tr) |
Copy constructor.
All the vertices and faces are duplicated. After the copy, this and tr refer to different triangulations: if tr is modified, this is not.
|
related |
Writes the triangulation t into the stream os.
Point.
|
related |
Reads a triangulation from stream is and assigns it to t.
Point.