|
CGAL 4.12.1 - 2D and 3D Linear Geometry Kernel
|
|
CGAL 4.12.1 - 2D and 3D Linear Geometry Kernel
|
AdaptableFunctor (with two arguments) Operations | |
| Kernel::Point_3 | operator() (const Kernel::Segment_3 &s, int i) |
returns source or target of s: fo(s,0) returns the source of s, fo(s,1) returns the target of s. More... | |
| Kernel::Point_3 | operator() (const Kernel::Iso_cuboid_3 &c, int i) |
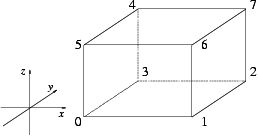
returns the i'th vertex of c, as indicated in the figure below. More... | |
| Kernel::Point_3 | operator() (const Kernel::Triangle_3 &t, int i) |
returns the i'th vertex of t. More... | |
| Kernel::Point_3 | operator() (const Kernel::Tetrahedron_3 &t, int i) |
returns the i'th vertex of t. More... | |
| Kernel::Point_3 Kernel::ConstructVertex_3::operator() | ( | const Kernel::Segment_3 & | s, |
| int | i | ||
| ) |
returns source or target of s: fo(s,0) returns the source of s, fo(s,1) returns the target of s.
The parameter i is taken modulo 2.
| Kernel::Point_3 Kernel::ConstructVertex_3::operator() | ( | const Kernel::Iso_cuboid_3 & | c, |
| int | i | ||
| ) |
returns the i'th vertex of c, as indicated in the figure below.
The parameter i is taken modulo 8.
| Kernel::Point_3 Kernel::ConstructVertex_3::operator() | ( | const Kernel::Triangle_3 & | t, |
| int | i | ||
| ) |
returns the i'th vertex of t.
The parameter i is taken modulo 3.
| Kernel::Point_3 Kernel::ConstructVertex_3::operator() | ( | const Kernel::Tetrahedron_3 & | t, |
| int | i | ||
| ) |
returns the i'th vertex of t.
The parameter i is taken modulo 4.