|
CGAL 4.12.1 - Point Set Shape Detection
|
|
CGAL 4.12.1 - Point Set Shape Detection
|
This CGAL component implements two algorithms for shape detection:
From an unstructured point set with unoriented normals, these algorithms detect a set of shapes (see Figure 72.1). Five types of primitive shapes are provided by this package: plane, sphere, cylinder, cone and torus. Other types of primitive shapes can also be added by the user.
Note that at the moment, region growing only detects planes.
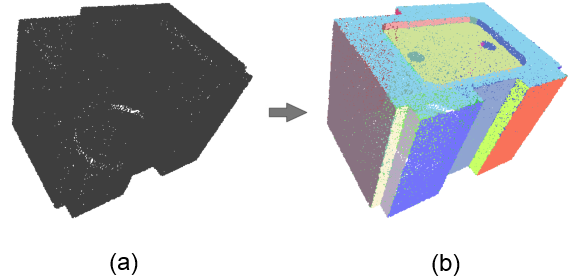
Both methods take as input a point set with unoriented normals and provide as output a set of detected shapes with associated input points. The output of the shape detection algorithms is a set of detected shapes with assigned points and all remaining points not covered by these shapes. Each input point can be assigned to at most one detected shape.
The shapes are detected via a RANSAC-type approach, i.e., a random sample consensus. The basic RANSAC approach repeats the following steps: (1) Randomly select samples from the input points. (2) Fit a shape to the selected samples. (3) Count the number of inliers to the shape, inliers being within a user-specified error tolerance to the shape. Steps 1-3 are repeated for a prescribed number of iterations and the shape with highest number of inliers, referred to as largest shape, is kept.
In our context, the error between a point and a shape is defined by its distance and normal deviation to the shape. A random subset corresponds to the minimal number of points (with normals) required to uniquely define a primitive.
For very large point sets the basic RANSAC method is not practical when testing all possible shape candidates against the input data in order to find the largest shape. The main idea behind the efficient RANSAC method consists in testing shape candidates against subsets of the input data. Shape candidates are constructed until the probability to miss the largest candidate is lower than a user-specified parameter. The largest shape is repeatedly extracted until no more shapes, restricted to cover a minimum number of points, can be extracted. An additional gain in efficiency is achieved through exploiting the normal attributes during initial shape construction and enumeration of inliers.
The support of a shape refers to the footprint of the points covered by the primitive. To avoid generating shapes with fragmented support we enforce a connectivity constraint by considering only one connected component, referred to as cluster, selected as the one covering the largest number of inliers. See Section Parameters for more details.
Planes are detected by growing planar regions from estimated planar seeds. First, points are sorted by a local planarity measure (the fitting quality returned by linear_least_squares_fitting_3()), such that points whose local neighborhood is the most planar are treated first.
The following steps are repeated: (1) Pick the next available point in the sorted list. (2) Initialize a plane tangent to this point and perpendicular to the normal vector of this point. (3) Compute the local neighborhood of the point with a user-specified radius. (4) Find inliers among these points, i.e. points that are within a user-specified error tolerance to the plane (and with a normal deviation within a user-specified tolerance to the normal of the plane). Steps 3-4 are repeated until no other inlier can be added. The plane is periodically reestimated by principal component analysis using all the inliers. If, after the growing, the plane has less inliers than a user-specified minimum number of points, it is discarded and the points are made available for other shapes to take once again.
The efficient RANSAC is a very quick method. Because it is based on randomness, it is not deterministic and some small shapes might be missed in the detection process.
Region growing usually takes longer than the efficient RANSAC but may provide better quality output in the presence of large scenes with numerous small details: as it iterates throughout all points of the scene, there are less chances of missing a shape. In addition, it is deterministic (for a given input and a given set of parameters, it always returns the same output, whereas as RANSAC uses randomness to detect shapes, the output of a RANSAC algorithm may vary). See figure Figure 72.2.

The algorithms have four parameters that are common. They have the same effects on the output for both RANSAC and region growing.
epsilon and normal_threshold: The error between a point-with-normal \(p\) and a shape \(S\) is defined by its Euclidean distance and normal deviation to \(S\). The normal deviation is computed between the normal at \(p\) and the normal of \(S\) at the closest projection of \(p\) onto \(S\). Parameter epsilon defines the absolute maximum tolerance Euclidean distance between a point and a shape. A high value for epsilon leads to the detection of fewer large shapes and hence a less detailed detection. A low value for epsilon yields a more detailed detection, but may lead to either lower coverage or over-segmentation. Over-segmentation translates into detection of fragmented shapes when epsilon is within or below the noise level. When the input point set is made of free-form parts, a higher tolerance epsilon allows for detecting more primitive shapes that approximate some of the free-form surfaces. The impact of this parameter is depicted by Figure Figure 72.3. Its impact on performance is evaluated in Section Performances. 
cluster_epsilon: The region growing algorithm uses cluster_epsilon to compute the neighborhood around points when growing the regions while the efficient RANSAC uses this parameter to cluster the points into connected components covered by a detected shape. For developable shapes that admit a trivial planar parameterization (plane, cylinder, cone) the points covered by a shape are mapped to a 2D parameter space chosen to minimize distortion and best preserve arc-length distances. This 2D parameter space is discretized using a regular grid, and a connected component search is performed to identify the largest cluster. Parameter cluster_epsilon defines the spacing between two cells of the regular grid, so that two points separated by a distance of at most \(2\sqrt{2}\), cluster_epsilon are considered adjacent. For non-developable shapes the connected components are identified by computing a neighboring graph in 3D and walking in the graph. The impact of parameter cluster_epsilon is depicted by Figure Figure 72.4.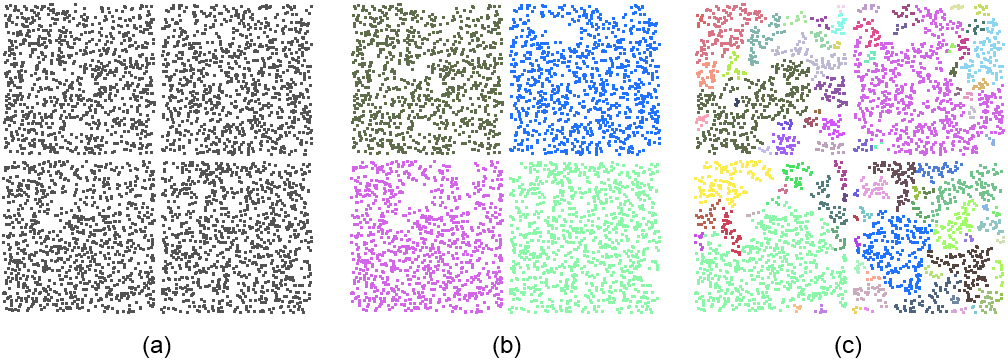
min_points: This minimum number of points controls the termination of the algorithm. The shape search is iterated until no further shapes can be found with a higher support. Note that for efficient RANSAC, this parameter is not strict: depending on the chosen probability, shapes may be extracted with a number of points lower than the specified parameter.In addition, the efficient RANSAC has a fifth parameter:
probability: This parameter defines the probability to miss the largest candidate shape. A lower probability provides a higher reliability and determinism at the cost of longer running times due to higher search endurance.The main classes Shape_detection_3::Efficient_RANSAC and Shape_detection_3::Region_growing take a template parameter Shape_detection_3::Shape_detection_traits that defines the geometric types and input format. Property maps provide a means to interface with user-specific data structures. The first parameter of the Shape_detection_3::Shape_detection_traits class is the common Kernel. In order to match the constraints of property maps, an iterator type and two maps that map an iterator to a point and a normal are specified in the Shape_detection_3::Shape_detection_traits class. The concept behind property maps is detailed in CGAL and Propery Maps.
Typical usage consists of five steps:
The following minimal example reads a point set from a file and detects only planar shapes. The default parameters are used for detection.
File Point_set_shape_detection_3/shape_detection_basic.cpp
Both Region Growing and Efficient RANSAC provide a callback mechanism that enables the user to track the progress of the algorithms. It can be used, for example, to terminate the algorithm based on a timeout. In the following example, the algorithm stops if it takes more than half a second and prints out the progress made:
File Point_set_shape_detection_3/shape_detection_with_callback.cpp
This example illustrates the user selection of parameters using the Shape_detection_3::Efficient_RANSAC::Parameters class. Shape detection is performed on five types of shapes (plane, cylinder, sphere, cone, torus). The input point set is sampled on a surface mostly composed of piece-wise planar and cylindrical parts, in addition to free-form parts.
Basic information of the detected shapes is written to the standard output: if the plane is either a plane or a cylinder, specific parameters are recovered, otherwise the general method info() is used to get the shape parameters in a string object. Note that specific parameters can be recovered for any of the provided shape.
File Point_set_shape_detection_3/efficient_RANSAC_parameters.cpp
This example illustrates how to access the points assigned to each shape and compute the mean error. A timer measures the running performance.
File Point_set_shape_detection_3/efficient_RANSAC_point_access.cpp
Other types of shapes can be detected by implementing a shape class derived from the class Shape_base and registering it to the shape detection factory of the efficient RANSAC object. This class must provide the following functions: construct a shape from a small set of given points, compute the squared distance from a query point and the shape and compute the normal deviation between a query point with normal and the normal to the shape at the closest point from the query. The used shape parameters are added as members to the derived class.
Note that the RANSAC approach is efficient for shapes that are uniquely defined by a small number of points, denoted by the number of required samples. The algorithm aims at detected the largest shape via many random samples, and the combinatorial complexity of possible samples increases rapidly with the number of required samples.
More specifically, the functions to be implemented are defined in the base class Shape_detection_3::Shape_base:
Shape_detection_3::Shape_base::minimum_sample_size() const: Returns the minimal number of required samples.Shape_detection_3::Shape_base::create_shape(const std::vector<size_t> &indices): The randomly generated samples are provided via a vector of indices. Shape_detection_3::Shape_base::point(size_t i) and Shape_detection_3::Shape_base::normal(size_t i) are used to retrieve the actual points and normals (see example below). The provided number of samples might actually be larger than the set minimal number of required samples, depending on the other types of shape types. If the provided samples are not sufficient to define a unique shape, e.g., in a degenerated case the shape is considered invalid.Shape_detection_3::Shape_base::squared_distance(const Point &p) const: This function computes the squared distance from a query point to the shape. It is used for traversing the hierarchical spatial data structure.Shape_detection_3::Shape_base::squared_distance(std::vector<FT> &dists, const std::vector<size_t> &indices)Shape_detection_3::Shape_base::cos_to_normal(const std::vector<size_t> &indice, sstd::vector<FT> &angles) const: These functions are used to determine the number of inlier points to the shape. They compute respectively the squared distance from a set of points to the shape, and the dot product between the point's normals and the normals at the shape for the closest points on the shape. The access to the actual point and normal data is carried out via Shape_detection_3::Shape_base::point(size_t i) and Shape_detection_3::Shape_base::normal(size_t i) (see example below). The resulting squared distance/dot product is stored in the vector provided as the first argument.By default the connected component is detected via the neighbor graph as mentioned above. However, for shapes that admit a faster approach to detect a connected component, the user can provide his/her own implementation to extract the connected component via:
Shape_detection_3::Shape_base::connected_component(std::vector<std::size_t>& indices, FT cluster_epsilon): The indices of all supporting points are stored in the vector indices. All points not belonging to the largest cluster of points are removed from the vector indices.Another optional method can be implemented to provide a helper function providing the shape parameters written to a string:
Shape_detection_3::Shape_base::info(): This function returns a string suitable for printing the shape parameters into a log/console. The default solution provides an empty string.The property maps are used to map the indices to the corresponding points and normals. The following example shows an implementation of a planar shape primitive, which is used by the example Point_set_shape_detection_3/efficient_RANSAC_custom_shape.cpp.
File Point_set_shape_detection_3/efficient_RANSAC_custom_shape.h
Shape detection applies to man-made scenes or objects such as urban scenes or scans of mechanical parts. Such scenes often contain a wide range of geometric regularities such as parallelism, orthogonality, or symmetry. This package offers a function to reinforce four types of regularities for planar shapes: CGAL::regularize_planes():
The user can choose to only regularize one or several of these 4 properties (see reference manual)). The process is greedy and based on a hierarchical decomposition (coplanar clusters are subgroups of parallel clusters which are subgroups of axis-symmetric and orthogonal clusters) as described by Verdie et al. [3]
File Point_set_shape_detection_3/plane_regularization.cpp
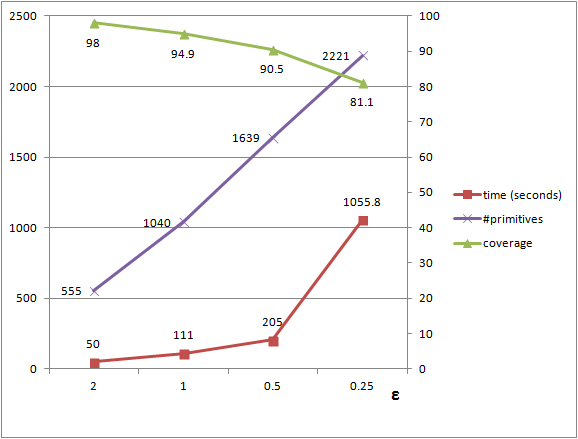
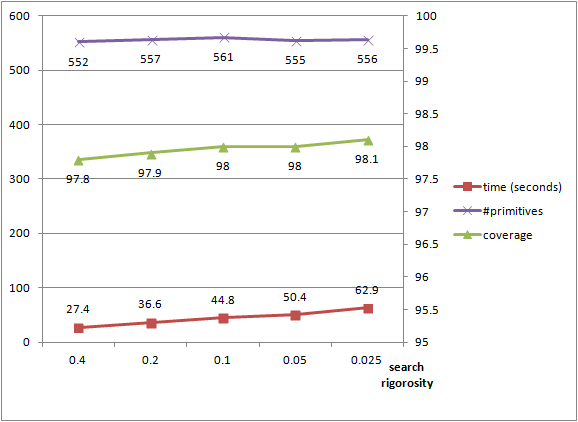
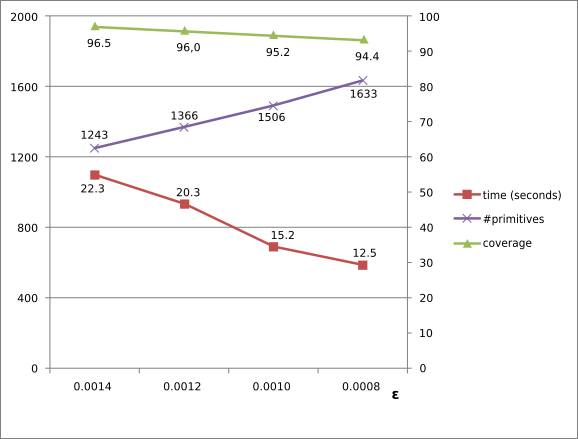
The running time and detection performance of the efficient RANSAC depend on the chosen parameters. A selective error tolerance parameter leads to higher running times and smaller shapes, as many shape candidates are generated to find the largest shape. We plot the detection performance against the epsilon error tolerance parameter for detecting planes in a complex scene with 5M points, see Figure 72.5. The probability parameter controls the endurance when searching for the largest candidate at each iteration. It barely impacts the number of detected shapes, has a moderate impact on the size of the detected shapes and increases the running times. We plot the performance against the probability parameter, see Figure 72.6.
Region growing iterates through every single point in the input, which makes it usually slower (although more robust). The main parameter that has an effect on running times is the epsilon used for clustering: internally, range queries are perform using spheres with radius cluster_epsilon. Using larger values means using larger spheres which are more computationally demanding.
We plot again the detection performance against the epsilon parameter for detecting planes, this time in a scene of 500k points, see figure Figure 72.7.
The efficient RANSAC implementation was developed by Sven Oesau based on a prototype version by Yannick Verdie, with the help of Clément Jamin and under the supervision of Pierre Alliez. Plane regularization and region growing were added by Simon Giraudot based on prototype versions developed by Florent Lafarge.