Definition

This AdaptableBinaryFunction computes the resultant of two polynomials \( f\) and \( g\) of type PolynomialTraits_d::Polynomial_d with respect to a certain variable.

Note that this functor operates on the polynomial in the univariate view, that is, the polynomial is considered as a univariate polynomial in one specific variable.

Let \( f\) and \( g\) be two univariate polynomials over some commutative ring \( A\), where

\[ f = f_mx^m + \dots + f_0 \]

and

\[ g = g_nx^n + \dots + g_0. \]

The resultant of \( f\) and \( g\) is defined as the determinant of the Sylvester matrix:

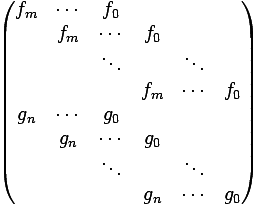
Note that this is a \( (n+m)\times(n+m)\) matrix as there are \( n\) rows for \( f\) and \( m\) rows that are used for \( g\). The blank spaces are supposed to be filled with zeros.

Advanced

Let \( L\) be the algebraic closure of \( A\), and write \( f\) and \( g\) as

\[ f := f_m \ccProd{i=1}{m}{(x-\alpha_i)},\ \alpha_i \in L \]

and

\[ g := g_n \ccProd{j=1}{n}{(x-\beta_j)},\ \beta_i \in L, \]

then the resultant of \( f\) and \( g\) is (up to leading coefficients) the product of all pairwise differences of the roots of \( f\) and \( g\), namely

\[ res(f,g) = f_m^n g_n^m \ccProd{i=1}{m}{\ccProd{j=1}{n}{(\alpha_i-\beta_j)}}. \]

In particular, \( res(f,g) \neq 0\) iff \( f\) and \( g\) have a common factor with a positive degree in \( X\).

There are various ways to compute the resultant. Naive options are the computation of the resultant as the determinant of the Sylvester Matrix or the Bezout Matrix as well as the so called subresultant algorithm, which is a variant of the Euclidean Algorithm. More sophisticated methods may use modular arithmetic and interpolation. For more information we refer to, e.g., [2].

Refines:

AdaptableBinaryFunction

CopyConstructible

DefaultConstructible

See also: Polynomial_d; PolynomialTraits_d; PolynomialTraits_d::UnivariateContent; PolynomialTraits_d::PolynomialSubresultants; PolynomialTraits_d::PrincipalSubresultants

Types
typedef PolynomialTraits_d::Coefficient_type	result_type

typedef PolynomialTraits_d::Polynomial_d	first_argument_type

typedef PolynomialTraits_d::Polynomial_d	second_argument_type

Operations
result_type	operator() (first_argument_type f, second_argument_type g)
	Computes the resultant of \( f\) and \( g\), with respect to the outermost variable.

Definition

Types

Operations