\( \newcommand{\E}{\mathrm{E}} \) \( \newcommand{\A}{\mathrm{A}} \) \( \newcommand{\R}{\mathrm{R}} \) \( \newcommand{\N}{\mathrm{N}} \) \( \newcommand{\Q}{\mathrm{Q}} \) \( \newcommand{\Z}{\mathrm{Z}} \) \( \def\ccSum #1#2#3{ \sum_{#1}^{#2}{#3} } \def\ccProd #1#2#3{ \sum_{#1}^{#2}{#3} }\)
CGAL 4.14 - Manual
Polymorphic Return Types
Author
Stefan Schirra (stsch.nosp@m.irr@.nosp@m.mpi-s.nosp@m.b.mp.nosp@m.g.de)

For some geometric operations, the type of the result of the operation is not fixed a priori, but depends on the input. Intersection computation is a prime example. The standard object-oriented approach to this is defining a common base class for all possible result types and returning a reference or a pointer to an object of the result type by a reference or pointer to the base class. Then all the virtual member functions in the interface of the base class can be applied to the result object and the implementation corresponding to the actual result type is called. It is hard to define appropriate base class interface functions (besides draw()).

CGAL has chosen a different approach, since CGAL wants to avoid large class hierarchies. With the CGAL class Object, you can fake a common base class, see Figure 0.1.

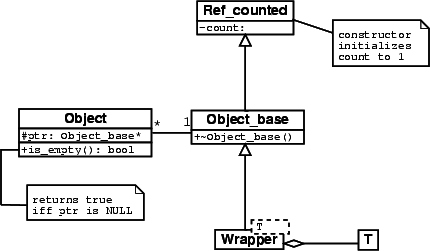
Object.png
Figure 0.1 UML class diagram for faked object hierarchies (since 2.2-I-4).

Functions having a polymorphic return type create an object of the actual result type and wrap it into an object of type Object. Refer to the documentation of CGAL::Object class for more details.

An alternative is to use a class handling several output iterators at the same time such as the classes CGAL::Dispatch_output_iterator. and CGAL::Dispatch_or_drop_output_iterator.