|
CGAL 4.14 - 3D Minkowski Sum of Polyhedra
|
|
CGAL 4.14 - 3D Minkowski Sum of Polyhedra
|

The Minkowski sum of two point sets \( P\) and \( Q\) in \( \mathbb{R}^d\), denoted by \( P \oplus Q\), is defined as the set \( \{p+q:p \in P, q \in Q \}\). Minkowski sums are used in a wide range of applications such as robot motion planning [3] and computer-aided design [2]. Figure 33.2 shows an example how Minkowski sums can be used to plan the motion of a translational robot. We want to know which are legal positions of the robot, and where can the robot go to from a specified starting position. If we model both the robot and the obstacles as a polyhedron and compute the Minkowski sum of the inverted robot (robot reflected at the origin) and the obstacles, then this Minkowski sum represents all illegal positions of the robot, i.e., all positions where it intersects the obstacle. Of course, the complement of that polyhedron describes all legal positions of the robot, i.e., all positions where it does not intersect an obstacle.
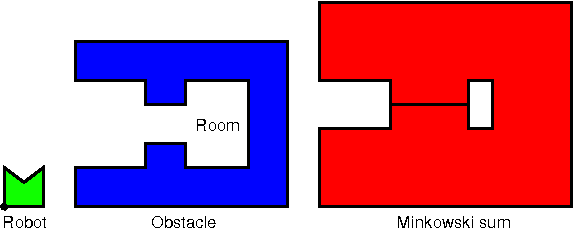
The Minkowski sum can be illustrated as follows. Pick an arbitrary reference point \( r\) of \( P\) (black dot in the lower left corner of the robot in Figure 33.2 ). Then place the inverted set \( -P\) on \( Q\), such that \( -r\) is on the boundary of \( Q\). Finally, move \( -P\) along the complete boundary of \( Q\). The union of \( Q\) and the points swept by \( -P\) is the Minkowski sum of \( P\) and \( Q\).
Implementing the Minkowski sum, the reference point does not need to be chosen. It is implicitly given as the origin of the coordinate system. Choosing a different reference point is equivalent to translating the coordinate system. Such a translation does not change the shape of the Minkowski sum; it only translates the Minkowski sum by the same vector.
This package provides a function minkowski_sum_3() that computes the Minkowski sum of two Nef polyhedra. We do not support arbitrary Nef polyhedra, yet. The restrictions are discussed in detail in Section Features and Restrictions.
The decomposition method for computing the Minkowski sum of non-convex polyhedra makes use of the fact that Minkowski sums of convex polyhedra are rather easy to compute. It decomposes both polyhedra into convex pieces, computes all pairwise Minkowski sums of the convex pieces, and merges the pairwise sums [1].
Minkowski sum are inherently complex to compute. Using the decomposition method, each polyhedron might be divided into a quadratic number of pieces, which is worst-case optimal. Then up to \( n^2m^2\) pairwise sums have to be computed and merged, where \( n\) and \( m\) are the complexities of the two input polyhedra (the complexity of a Nef_polyhedron_3 is the sum of its Vertices, Halfedges and SHalfedges). In total the operation runs in \( O(n^3m^3)\) time.
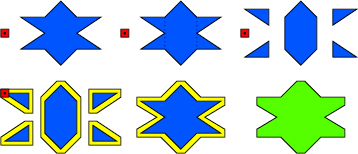
Since the computation of the Minkowski sum takes quite some time, we give the running times of some Minkowski sum computations. They were computed with CGAL 3.3 on a machine with a 2.4 GHz AMD Opteron processor and 4 GB RAM. The code was compiled with g++ 3.2 and compiler options -O2. The Nef_polyhedron_3 class was instantiated with the geometric kernel Homogeneous<leda_integer>. The Minkowski sum of the spoon and the star is illustrated in Figure 33.1.
| model 1 | model 2 | running | ||||
| name | facets | conv. pcs. | name | facets | conv. pcs. | time |
| mushroom | 448 | 255 | cube | 6 | 1 | 204s |
| mushroom | 448 | 255 | ball1 | 128 | 1 | 553s |
| spoon | 336 | 186 | star | 24 | 5 | 882s |
| cup | 1000 | 774 | ball2 | 1000 | 1 | 9851s |
minkowski_sum_3().This package was written to allow the computation of Minkowski sums of full-dimensional polyhedra even in so-called tight-passage scenarios. Tight passage scenarios occur in robot motion planning, when a robot is just as wide as a passage it needs to traverse. In these scenarios at least one polyhedron - the obstacles or the robot - must be modeled as an open set. Then the Minkowski sum will also be an open set and tight passages will occur as lower-dimensional exclusions, i.e., as facets, lines, or vertices that are, in contrast to the volume around them, not part of the resulting point set. Figure 33.2 shows such a tight passage scenario.
Our implementation uses Nef_polyhedron_3 to model the input polyhedra and the result polyhedron. An instance of Nef_polyhedron_3 represents a subdivision of the three-dimensional space into vertices, edges, facets, and volumes. Some of these items form the polyhedron (selected), while others represent the outer volume or holes within the polyhedron (unselected). As an example, the unit cube is the point set \( [0,1]^3\). The smallest subdivision that represents the unit cube has 8 vertices, 12 edges, 6 facets, and 2 volumes. The volumes enclosed by the vertices, edges, and facets is the interior of the cube and therefore selected. The volume outside the cube does not belong to it and is therefore unselected. The vertices, edges, and facets - also denoted as boundary items - are needed to separate the two volumes, but are also useful for representing topological properties. In case of the (closed) unit cube the boundary items are part of the polyhedron and therefore selected, but in case of the open unit cube \( [0,1)^3\) they are unselected. Each item has its own selection mark, which allows the correct representation of Nef polyhedra, which are closed under Boolean and topological operations. Details can be found in Chapter 3D Boolean Operations on Nef Polyhedra.
The use of Nef_polyhedron_3 allows many scenarios beyond the Minkowski sum of two solids. First, they can model the input and the result of a tight passage scenario, i.e., they can model open and closed solids as is needed for the input models, and they can model tight passages, which are lower-dimensional exclusions represented as unselected facets, edges, and vertices. We strive for extending the package to work for arbitrary 3D Nef polyhedra. In addition to the Minkowski sums of two solids, we added several features. At the moment we allow an input polyhedron to consist of:
Taking a different viewpoint, the implementation is restricted as follows:
The second restriction might seem a bit odd. It stems from the fact that the Minkowski sum on convex polyhedra can only handle polyhedra, whose sides consist of a single facet. The decomposition process usually yields complex adjacency relations between a convex part, its adjacent convex parts, and the outer volume. The side of a convex piece is then decomposed into several facets, each of which represents one of these adjacency relations. For the convex Minkowski sum, we ignore the decompositions of the sides, but need to find a common selection mark. If there are two facets that are adjacent to the outer volume, but have different selections marks, we cannot set a common selection mark without spoiling the correctness of the Minkowski sum.
The function minkowski_sum_3() should be used with the Exact_predicates_exact_constructions_kernel, which often is the most efficient choice and allows floating-point input. Consult Section File I/O for Nef Polyhedra for more details.
The following example code illustrates the usage of the function minkowski_sum_3(). Note that either input polyhedra will be modified by the function if it is non-convex. So, if they are needed further on, they need to be copied, first. The copying is not done by the function itself to keep the memory usage as small as possible.
File Minkowski_sum_3/cube_offset.cpp
With the function minkowski_sum_3() it is also possible to realize other interesting geometric operations like the glide operation, which computes the point set swept by a polyhedron that moves along a polygonal path. The following example shows how to construct a polygonal path and then compute the glide operation by calling the function minkowski_sum_3().
File Minkowski_sum_3/glide.cpp