2D Periodic Hyperbolic Triangulations Reference

Iordan Iordanov and Monique Teillaud

This package enables building and handling triangulations of point sets on the two dimensional hyperbolic Bolza surface. Triangulations are built incrementally and can be modified by insertion or removal of vertices. Point location facilities are also offered. The package provides Delaunay triangulations and offers primitives to build the dual Voronoi diagrams.

Introduced in: CGAL 4.14
Depends on: 2D Hyperbolic Delaunay Triangulations
BibTeX: cgal:i-p4ht2-17-19a
License: GPL
Windows Demo: Periodic Hyperbolic Delaunay Triangulation
Common Demo Dlls: dlls

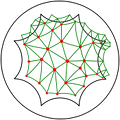
CGAL traditionally represents a triangulation via its faces and vertices. We represent a triangulation of the Bolza surface via the canonical representatives of its faces in the hyperbolic plane. This package provides the necessary objects and functions to work with Delaunay triangulations of the Bolza surface.

Each vertex gives access to one of its incident faces, and stores an input point. We additionally allow each vertex to store (temporarily) a hyperbolic translation to facilitate the insertion of new points and the removal of existing vertices.

Each face gives access to its three incident vertices and to its three adjacent faces. We enable a face to store additionally three hyperbolic translations. When applied to the three points stored in the vertices of the face, these translations produce the canonical representative of the face in the hyperbolic plane.

The three vertices of a face are indexed with 0, 1, and 2 in positive (counter-clockwise) orientation. The orientation of faces on the Bolza surface is defined as the orientation of their canonical representatives in the hyperbolic plane.

Classified Reference Pages

Concepts

• Periodic_4HyperbolicTriangulationTraits_2 adds supplementary requirements to the concept HyperbolicDelaunayTriangulationTraits_2 that are necessary for periodic hyperbolic triangulations.
• Periodic_4HyperbolicDelaunayTriangulationTraits_2 refines the concept Periodic_4HyperbolicTriangulationTraits_2 by adding requirements necessary for the computation of periodic hyperbolic Delaunay triangulations.
• Periodic_4HyperbolicTriangulationFaceBase_2 describes the requirements for faces to store hyperbolic translations.
• Periodic_4HyperbolicTriangulationVertexBase_2 describes the requirements for vertices to store hyperbolic translations.

Classes

• CGAL::Periodic_4_hyperbolic_triangulation_2 gives access to the elements of the triangulation (vertices, edges, and faces), and functionality common to triangulations in general, such as point location. This class does not support insertion or removal of points.
• CGAL::Periodic_4_hyperbolic_Delaunay_triangulation_2 enables the construction and modification of Delaunay triangulations of the Bolza surface.
• CGAL::Periodic_4_hyperbolic_Delaunay_triangulation_traits_2 is a model for the concept Periodic_4HyperbolicDelaunayTriangulationTraits_2.
• CGAL::Periodic_4_hyperbolic_triangulation_face_base_2 is a model of the concept Periodic_4HyperbolicTriangulationFaceBase_2 and represents a face of the triangulation.
• CGAL::Periodic_4_hyperbolic_triangulation_vertex_base_2 is a model of the concept Periodic_4HyperbolicTriangulationVertexBase_2 and represents a vertex of the triangulation.
• CGAL::Hyperbolic_octagon_translation is a class that represent hyperbolic translations of the fundamental group \(\mathcal G\) of the Bolza surface.

Modules
	Concepts
	Main Classes
	Traits Classes
	Vertex and Face Base Classes
	Hyperbolic Translations Classes