|
CGAL 4.4 - Point Set Processing
|
|
CGAL 4.4 - Point Set Processing
|
This CGAL component implements methods to analyze and process unorganized 3D point sets. The input is an unorganized 3D point set, possibly with normal attributes (unoriented or oriented). This point set can be analyzed to measure geometric properties such as average spacing between the points and their k nearest neighbors. It can be processed with functions devoted to the simplification, outlier removal, smoothing, normal estimation and normal orientation. The processing of point sets is often needed in applications dealing with measurement data, such as surface reconstruction from laser scanned data (see Figure 57.1).
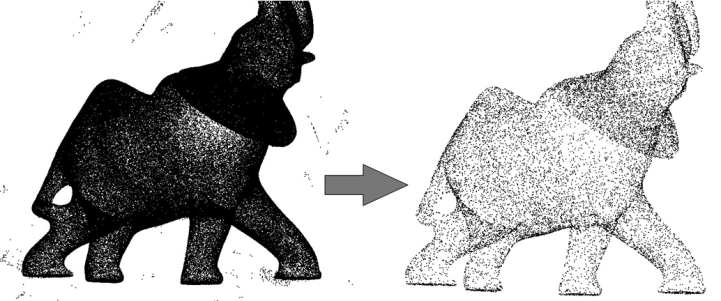
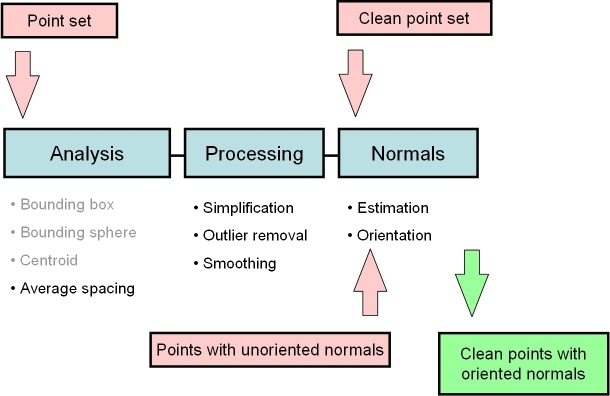
In the context of surface reconstruction we can position the elements of this component along the common surface reconstruction pipeline (Figure 57.2) which involves the following steps:
The algorithms of this component take as input parameters iterator ranges of 3D points, or of 3D points with normals. The property maps are used to access the point or normal information from the input data, so as to let the user decide upon the implementation of a point with normal. The latter can be represented as, e.g., a class derived from the CGAL 3D point, or as a std::pair<Point_3<K>, Vector_3<K>>, or as a boost::tuple<..,Point_3<K>, ..., Vector_3<K> >.
The following classes described in Chapter CGAL and Boost Property Maps provide property maps for the implementations of points with normals listed above:
Identity_property_map<T>First_of_pair_property_map<Pair> and Second_of_pair_property_map<Pair>Nth_of_tuple_property_map<N, Tuple>Identity_property_map<Point_3> is the default value of the position property map expected by all functions in this component.
See below examples using pair and tuple property maps.
Users of this package may use other types to represent positions and normals if they implement the corresponding property maps.
We provide functions to read and write sets of points or sets of points with normals from the following ASCII file formats: XYZ (three point coordinates x y z per line or three point coordinates and three normal vector coordinates x y z nx ny nz per line), and OFF (Object File Format) [2].
The following example reads a point set from an input file and writes it to a file, both in the XYZ format. Positions and normals are stored in pairs and accessed through property maps.
File Point_set_processing_3/read_write_xyz_point_set_example.cpp
Function compute_average_spacing() computes the average spacing of all input points to their k nearest neighbor points, k being specified by the user. As it provides an order of a point set density, this function is used downstream the surface reconstruction pipeline to automatically determine some parameters such as output mesh sizing for surface reconstruction.
The following example reads a point set in the xyz format and computes the average spacing. Index, position and color are stored in a tuple and accessed through property maps.
File Point_set_processing_3/average_spacing_example.cpp
Note that other functions such as centroid or bounding volumes are found in other CGAL components:
Function remove_outliers() deletes a user-specified fraction of outliers from an input point set. More specifically, it sorts the input points in increasing order of average squared distances to their k nearest neighbors and deletes the points with largest value.
The following example reads a point set and removes 5% of the points. It uses the Identity_property_map<Point_3> property map (optional as it is the default position property map of all functions in this component.)
File Point_set_processing_3/remove_outliers_example.cpp
Two simplification functions are devised to reduce an input point set, either randomly or using a grid-based clustering approach.
Function random_simplify_point_set() randomly deletes a user-specified fraction of points from the input point set. This algorithm is fast.
Function grid_simplify_point_set() considers a regular grid covering the bounding box of the input point set, and clusters all points sharing the same cell of the grid by picking as representant one arbitrarily chosen point. This algorithm is slower than random_simplify_point_set().
The following example reads a point set and simplifies it by clustering.
File Point_set_processing_3/grid_simplification_example.cpp

Function jet_smooth_point_set() smooths the input point set by projecting each point onto a smooth parametric surface patch (so-called jet surface) fitted over its k nearest neighbors.
The following example generates a set of 9 points close to the xy plane and smooths them using 8 nearest neighbors:
File Point_set_processing_3/jet_smoothing_example.cpp
Assuming a point set sampled over an inferred surface \( S\), two functions provide an estimate of the normal to \( S\) at each point. The result is an unoriented normal vector for each input point.
Function jet_estimate_normals() estimates the normal direction at each point from the input set by fitting a jet surface over its k nearest neighbors. The default jet is a quadric surface. This algorithm is well suited to point sets scattered over curved surfaces.
Function pca_estimate_normals() estimates the normal direction at each point from the set by linear least squares fitting of a plane over its k nearest neighbors. This algorithm is simpler and faster than jet_estimate_normals().
Function mst_orient_normals() orients the normals of a set of points with unoriented normals using the method described by Hoppe et al. in Surface reconstruction from unorganized points [1]. More specifically, this method constructs a Riemannian graph over the input points (the graph of the k nearest neighbor points) and propagates a seed normal orientation within a minimum spanning tree computed over this graph. The result is an oriented normal vector for each input unoriented normal, except for the normals which could not be successfully oriented.
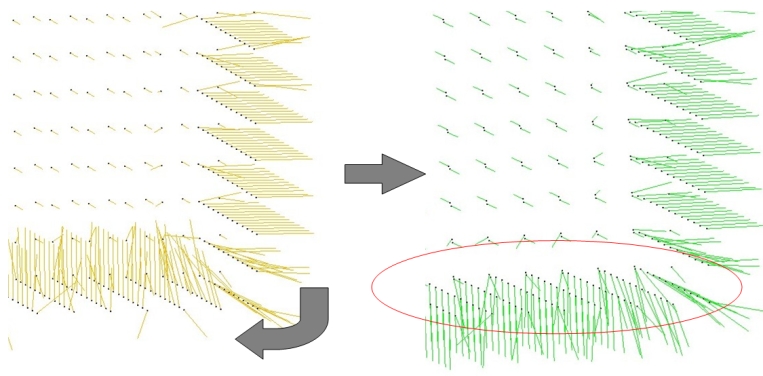
The following example reads a point set from a file, estimates the normals through PCA over the 6 nearest neighbors and orients the normals:
File Point_set_processing_3/normals_example.cpp