User Manual

Authors

Pierre Alliez, Laurent Saboret, Nader Salman

Introduction

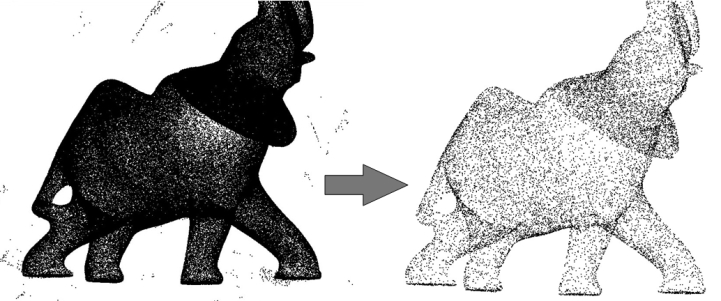
This CGAL component implements methods to analyze and process unorganized 3D point sets. The input is an unorganized 3D point set, possibly with normal attributes (unoriented or oriented). This point set can be analyzed to measure geometric properties such as average spacing between the points and their k nearest neighbors. It can be processed with functions devoted to the simplification, outlier removal, smoothing, normal estimation and normal orientation. The processing of point sets is often needed in applications dealing with measurement data, such as surface reconstruction from laser scanned data (see Figure 57.1).

Figure 57.1 Point set processing. Left: 275K points sampled on the statue of an elephant with a Minolta laser scanner. Right: point set after clean-up and simplification to 17K points.

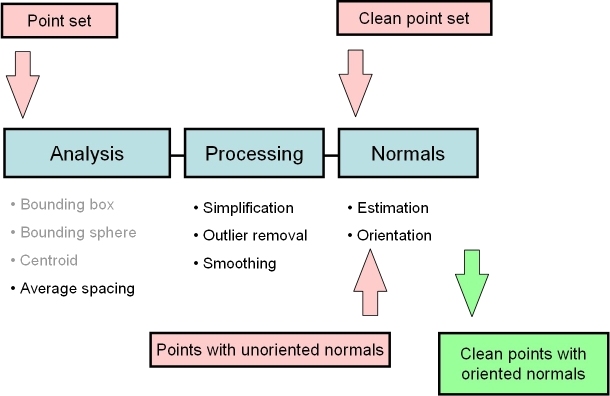
In the context of surface reconstruction we can position the elements of this component along the common surface reconstruction pipeline (Figure 57.2) which involves the following steps:

1. Scanning and scan alignment to produce a set of points or points with normals (alignment is not covered in CGAL);
2. Outlier removal;
3. Simplification to reduce the number of input points;
4. Smoothing to reduce noise in the input data;
5. Normal estimation and orientation when the normals are not already provided by the acquisition device; and
6. Surface reconstruction. Chapter Surface Reconstruction from Point Sets deals with surface reconstruction from point sets with normal attributes.

Figure 57.2 Point set processing pipeline for surface reconstruction. The algorithms listed in gray are available from other CGAL components (bounding volumes and principal component analysis).

Input/Output

Property Maps

The algorithms of this component take as input parameters iterator ranges of 3D points, or of 3D points with normals. The property maps are used to access the point or normal information from the input data, so as to let the user decide upon the implementation of a point with normal. The latter can be represented as, e.g., a class derived from the CGAL 3D point, or as a std::pair<Point_3<K>, Vector_3<K>>, or as a boost::tuple<..,Point_3<K>, ..., Vector_3<K> >.

The following classes described in Chapter CGAL and Boost Property Maps provide property maps for the implementations of points with normals listed above:

• Identity_property_map<T>
• First_of_pair_property_map<Pair> and Second_of_pair_property_map<Pair>
• Nth_of_tuple_property_map<N, Tuple>

Identity_property_map<Point_3> is the default value of the position property map expected by all functions in this component.

See below examples using pair and tuple property maps.

Users of this package may use other types to represent positions and normals if they implement the corresponding property maps.

Streams

We provide functions to read and write sets of points or sets of points with normals from the following ASCII file formats: XYZ (three point coordinates x y z per line or three point coordinates and three normal vector coordinates x y z nx ny nz per line), and OFF (Object File Format) [2].

• read_xyz_points()
• read_off_points()
• write_off_points()
• write_xyz_points()

Example

The following example reads a point set from an input file and writes it to a file, both in the XYZ format. Positions and normals are stored in pairs and accessed through property maps.
File Point_set_processing_3/read_write_xyz_point_set_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>
#include <CGAL/IO/write_xyz_points.h>

#include <utility> // defines std::pair
#include <vector>
#include <fstream>

// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;

// Point with normal vector stored as a std::pair.
typedef std::pair<Point, Vector> Pwn;

int main(void)
{
    // Reads a .xyz point set file in points[].
    // Note: read_xyz_points_and_normals() requires an output iterator
    // over points and as well as property maps to access each
    // point position and normal.
    std::vector<Pwn> points;
    std::ifstream in("data/oni.xyz");
    if (!in ||
        !CGAL::read_xyz_points_and_normals(
            in,std::back_inserter(points),
            CGAL::First_of_pair_property_map<Pwn>(),
            CGAL::Second_of_pair_property_map<Pwn>()))
    {
      std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
      return EXIT_FAILURE;
    }

    // Saves point set.
    // Note: write_xyz_points_and_normals() requires an output iterator
    // over points as well as property maps to access each
    // point position and normal.
    std::ofstream out("oni_copy.xyz");
    if (!out ||
        !CGAL::write_xyz_points_and_normals(
            out, points.begin(), points.end(),
            CGAL::First_of_pair_property_map<Pwn>(),
            CGAL::Second_of_pair_property_map<Pwn>()))
    {
      return EXIT_FAILURE;
    }

    return EXIT_SUCCESS;
}

Analysis

Function compute_average_spacing() computes the average spacing of all input points to their k nearest neighbor points, k being specified by the user. As it provides an order of a point set density, this function is used downstream the surface reconstruction pipeline to automatically determine some parameters such as output mesh sizing for surface reconstruction.

Example

The following example reads a point set in the xyz format and computes the average spacing. Index, position and color are stored in a tuple and accessed through property maps.
File Point_set_processing_3/average_spacing_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/compute_average_spacing.h>
#include <CGAL/IO/read_xyz_points.h>

#include <vector>
#include <fstream>
#include <boost/tuple/tuple.hpp>

// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT FT;
typedef Kernel::Point_3 Point;

// Data type := index, followed by the point, followed by three integers that
// define the Red Green Blue color of the point.
typedef boost::tuple<int, Point, int, int, int> IndexedPointWithColorTuple;

int main(void)
{
    // Reads a .xyz point set file in points.
    // As the point is the second element of the tuple (that is with index 1)
    // we use a property map that accesses the 1st element of the tuple.
    std::vector<IndexedPointWithColorTuple> points;
    std::ifstream stream("data/sphere_20k.xyz");
    if (!stream ||
        !CGAL::read_xyz_points(
            stream, std::back_inserter(points),
            CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>()))
    {
      std::cerr << "Error: cannot read file data/sphere_20k.xyz" << std::endl;
      return EXIT_FAILURE;
    }

    // Initialize index and RGB color fields in tuple.
    // As the index and RGB color are respectively the first and third-fifth elements
    // of the tuple we use a get function from the property map that accesses the 0
    // and 2-4th elements of the tuple.
    for(unsigned int i = 0; i < points.size(); i++)
    {
      points[i].get<0>() = i;   // set index value of tuple to i

      points[i].get<2>() = 0;   // set RGB color to black
      points[i].get<3>() = 0;
      points[i].get<4>() = 0;
    }

    // Computes average spacing.
    const unsigned int nb_neighbors = 6; // 1 ring
    FT average_spacing = CGAL::compute_average_spacing(
                            points.begin(), points.end(),
                            CGAL::Nth_of_tuple_property_map<1,IndexedPointWithColorTuple>(),
                            nb_neighbors);
    std::cout << "Average spacing: " << average_spacing << std::endl;

    return EXIT_SUCCESS;
}

Note that other functions such as centroid or bounding volumes are found in other CGAL components:

• centroid()
• bounding_box()
• Min_sphere_of_spheres_d<Traits>

Outlier Removal

Function remove_outliers() deletes a user-specified fraction of outliers from an input point set. More specifically, it sorts the input points in increasing order of average squared distances to their k nearest neighbors and deletes the points with largest value.

Example

The following example reads a point set and removes 5% of the points. It uses the Identity_property_map<Point_3> property map (optional as it is the default position property map of all functions in this component.)
File Point_set_processing_3/remove_outliers_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/property_map.h>
#include <CGAL/remove_outliers.h>
#include <CGAL/IO/read_xyz_points.h>

#include <vector>
#include <fstream>

// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;

int main(void)
{
  // Reads a .xyz point set file in points[].
  // The Identity_property_map property map can be omitted here as it is the default value.
  std::vector<Point> points;
  std::ifstream stream("data/oni.xyz");
  if (!stream ||
      !CGAL::read_xyz_points(stream, std::back_inserter(points),
        CGAL::Identity_property_map<Point>()))
  {
    std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
    return EXIT_FAILURE;
  }

  // Removes outliers using erase-remove idiom.
  // The Identity_property_map property map can be omitted here as it is the default value.
  const double removed_percentage = 5.0; // percentage of points to remove
  const int nb_neighbors = 24; // considers 24 nearest neighbor points
  points.erase(CGAL::remove_outliers(points.begin(), points.end(),
                  CGAL::Identity_property_map<Point>(),
                  nb_neighbors, removed_percentage), 
               points.end());

  // Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
  std::vector<Point>(points).swap(points);

  return EXIT_SUCCESS;
}

Simplification

Two simplification functions are devised to reduce an input point set, either randomly or using a grid-based clustering approach.

Function random_simplify_point_set() randomly deletes a user-specified fraction of points from the input point set. This algorithm is fast.

Function grid_simplify_point_set() considers a regular grid covering the bounding box of the input point set, and clusters all points sharing the same cell of the grid by picking as representant one arbitrarily chosen point. This algorithm is slower than random_simplify_point_set().

Example

The following example reads a point set and simplifies it by clustering.
File Point_set_processing_3/grid_simplification_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/grid_simplify_point_set.h>
#include <CGAL/IO/read_xyz_points.h>

#include <vector>
#include <fstream>

// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;

int main(void)
{
  // Reads a .xyz point set file in points[].
  std::vector<Point> points;
  std::ifstream stream("data/oni.xyz");
  if (!stream ||
      !CGAL::read_xyz_points(stream, std::back_inserter(points)))
  {
    std::cerr << "Error: cannot read file data/oni.xyz" << std::endl;
    return EXIT_FAILURE;
  }

  // simplification by clustering using erase-remove idiom
  double cell_size = 0.001;
  points.erase(CGAL::grid_simplify_point_set(points.begin(), points.end(), cell_size),
               points.end());

  // Optional: after erase(), use Scott Meyer's "swap trick" to trim excess capacity
  std::vector<Point>(points).swap(points);

  return EXIT_SUCCESS;
}

Figure 57.3 Point set simplification through grid-based clustering. Removed points are depicted in red. Notice how low-density areas (in green) are not simplified.

Smoothing

Function jet_smooth_point_set() smooths the input point set by projecting each point onto a smooth parametric surface patch (so-called jet surface) fitted over its k nearest neighbors.

Example

The following example generates a set of 9 points close to the xy plane and smooths them using 8 nearest neighbors:
File Point_set_processing_3/jet_smoothing_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/jet_smooth_point_set.h>
#include <vector>

// types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;

int main(void)
{
  // generate point set
  std::vector<Point> points;
  points.push_back(Point( 0.0, 0.0, 0.001));
  points.push_back(Point(-0.1,-0.1, 0.002));
  points.push_back(Point(-0.1,-0.2, 0.001));
  points.push_back(Point(-0.1, 0.1, 0.002));
  points.push_back(Point( 0.1,-0.1, 0.000));
  points.push_back(Point( 0.1, 0.2, 0.001));
  points.push_back(Point( 0.2, 0.0, 0.002));
  points.push_back(Point( 0.2, 0.1, 0.000));
  points.push_back(Point( 0.0,-0.1, 0.001));

  // Smoothing.
  const unsigned int nb_neighbors = 8; // default is 24 for real-life point sets
  CGAL::jet_smooth_point_set(points.begin(), points.end(), nb_neighbors);

  return EXIT_SUCCESS;
}

Normal Estimation

Assuming a point set sampled over an inferred surface \( S\), two functions provide an estimate of the normal to \( S\) at each point. The result is an unoriented normal vector for each input point.

Function jet_estimate_normals() estimates the normal direction at each point from the input set by fitting a jet surface over its k nearest neighbors. The default jet is a quadric surface. This algorithm is well suited to point sets scattered over curved surfaces.

Function pca_estimate_normals() estimates the normal direction at each point from the set by linear least squares fitting of a plane over its k nearest neighbors. This algorithm is simpler and faster than jet_estimate_normals().

Normal Orientation

Function mst_orient_normals() orients the normals of a set of points with unoriented normals using the method described by Hoppe et al. in Surface reconstruction from unorganized points [1]. More specifically, this method constructs a Riemannian graph over the input points (the graph of the k nearest neighbor points) and propagates a seed normal orientation within a minimum spanning tree computed over this graph. The result is an oriented normal vector for each input unoriented normal, except for the normals which could not be successfully oriented.

Figure 57.4 Normal orientation of a sampled cube surface. Left: unoriented normals. Right: orientation of right face normals is propagated to bottom face.

Example

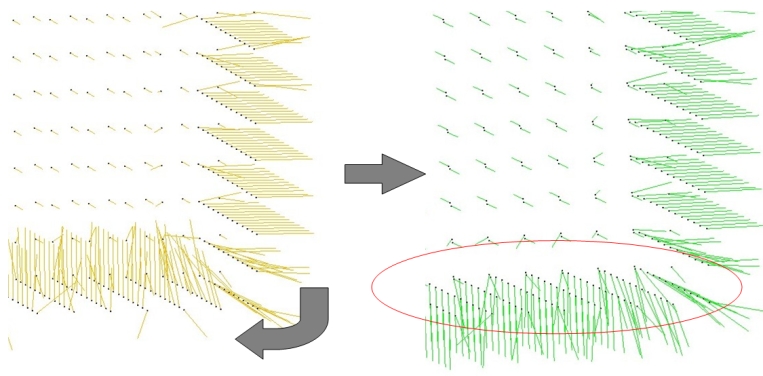
The following example reads a point set from a file, estimates the normals through PCA over the 6 nearest neighbors and orients the normals:
File Point_set_processing_3/normals_example.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/pca_estimate_normals.h>
#include <CGAL/mst_orient_normals.h>
#include <CGAL/property_map.h>
#include <CGAL/IO/read_xyz_points.h>

#include <utility> // defines std::pair
#include <list>
#include <fstream>

// Types
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::Point_3 Point;
typedef Kernel::Vector_3 Vector;

// Point with normal vector stored in a std::pair.
typedef std::pair<Point, Vector> PointVectorPair;

int main(void)
{
    // Reads a .xyz point set file in points[].
    std::list<PointVectorPair> points;
    std::ifstream stream("data/sphere_20k.xyz");
    if (!stream ||
        !CGAL::read_xyz_points(stream,
                               std::back_inserter(points),
                               CGAL::First_of_pair_property_map<PointVectorPair>()))
    {
        std::cerr << "Error: cannot read file data/sphere_20k.xyz" << std::endl;
        return EXIT_FAILURE;
    }

    // Estimates normals direction.
    // Note: pca_estimate_normals() requires an iterator over points
    // as well as property maps to access each point's position and normal.
    const int nb_neighbors = 18; // K-nearest neighbors = 3 rings
    CGAL::pca_estimate_normals(points.begin(), points.end(),
                               CGAL::First_of_pair_property_map<PointVectorPair>(),
                               CGAL::Second_of_pair_property_map<PointVectorPair>(),
                               nb_neighbors);

    // Orients normals.
    // Note: mst_orient_normals() requires an iterator over points
    // as well as property maps to access each point's position and normal.
    std::list<PointVectorPair>::iterator unoriented_points_begin =
        CGAL::mst_orient_normals(points.begin(), points.end(),
                                 CGAL::First_of_pair_property_map<PointVectorPair>(),
                                 CGAL::Second_of_pair_property_map<PointVectorPair>(),
                                 nb_neighbors);

    // Optional: delete points with an unoriented normal
    // if you plan to call a reconstruction algorithm that expects oriented normals.
    points.erase(unoriented_points_begin, points.end());

    return EXIT_SUCCESS;
}