\( \newcommand{\E}{\mathrm{E}} \) \( \newcommand{\A}{\mathrm{A}} \) \( \newcommand{\R}{\mathrm{R}} \) \( \newcommand{\N}{\mathrm{N}} \) \( \newcommand{\Q}{\mathrm{Q}} \) \( \newcommand{\Z}{\mathrm{Z}} \) \( \def\ccSum #1#2#3{ \sum_{#1}^{#2}{#3} } \def\ccProd #1#2#3{ \sum_{#1}^{#2}{#3} }\)
CGAL 4.6.1 - 2D and 3D Linear Geometry Kernel
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Groups Pages
List of all members
CGAL::Iso_cuboid_3< Kernel > Class Template Reference
3D Kernel Objects

#include <CGAL/Iso_cuboid_3.h>

Definition

An object c of the data type Iso_cuboid_3 is a cuboid in the Euclidean space \( \E^3\) with edges parallel to the \( x\), \( y\) and \( z\) axis of the coordinate system.

Although they are represented in a canonical form by only two vertices, namely the lexicographically smallest and largest vertex with respect to Cartesian \( xyz\) coordinates, we provide functions for "accessing" the other vertices as well.

Iso-oriented cuboids and bounding boxes are quite similar. The difference however is that bounding boxes have always double coordinates, whereas the coordinate type of an iso-oriented cuboid is chosen by the user.

See Also
Kernel::IsoCuboid_3

Creation

 Iso_cuboid_3 (const Point_3< Kernel > &p, const Point_3< Kernel > &q)
 introduces an iso-oriented cuboid c with diagonal opposite vertices p and q. More...
 
 Iso_cuboid_3 (const Point_3< Kernel > &p, const Point_3< Kernel > &q, int)
 introduces an iso-oriented cuboid c with diagonal opposite vertices p and q. More...
 
 Iso_cuboid_3 (const Point_3< Kernel > &left, const Point_3< Kernel > &right, const Point_3< Kernel > &bottom, const Point_3< Kernel > &top, const Point_3< Kernel > &far, const Point_3< Kernel > &close)
 introduces an iso-oriented cuboid c whose minimal \( x\) coordinate is the one of left, the maximal \( x\) coordinate is the one of right, the minimal \( y\) coordinate is the one of bottom, the maximal \( y\) coordinate is the one of top, the minimal \( z\) coordinate is the one of far, the maximal \( z\) coordinate is the one of close.
 
 Iso_cuboid_3 (const Kernel::RT &min_hx, const Kernel::RT &min_hy, const Kernel::RT &min_hz, const Kernel::RT &max_hx, const Kernel::RT &max_hy, const Kernel::RT &max_hz, const Kernel::RT &hw=RT(1))
 introduces an iso-oriented cuboid c with diagonal opposite vertices (min_hx/hw, min_hy/hw, min_hz/hw) and (max_hx/hw, max_hy/hw, max_hz/hw). More...
 
 Iso_cuboid_3 (const Bbox_3 &bbox)
 If Kernel::RT is constructible from double, introduces an iso-oriented cuboid from bbox.
 

Operations

bool operator== (const Iso_cuboid_3< Kernel > &c2) const
 Test for equality: two iso-oriented cuboid are equal, iff their lower left and their upper right vertices are equal.
 
bool operator!= (const Iso_cuboid_3< Kernel > &c2) const
 Test for inequality.
 
Point_3< Kernel > vertex (int i) const
 returns the i'th vertex modulo 8 of c. More...
 
Point_3< Kernel > operator[] (int i) const
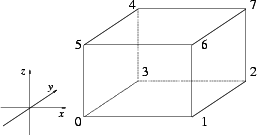
 returns vertex(i), as indicated in the figure below: More...
 
Point_3< Kernel > min () const
 returns the smallest vertex of c (= vertex(0)).
 
Point_3< Kernel > max () const
 returns the largest vertex of c (= vertex(7)).
 
Kernel::FT xmin () const
 returns smallest Cartesian \( x\)-coordinate in c.
 
Kernel::FT ymin () const
 returns smallest Cartesian \( y\)-coordinate in c.
 
Kernel::FT zmin () const
 returns smallest Cartesian \( z\)-coordinate in c.
 
Kernel::FT xmax () const
 returns largest Cartesian \( x\)-coordinate in c.
 
Kernel::FT ymax () const
 returns largest Cartesian \( y\)-coordinate in c.
 
Kernel::FT zmax () const
 returns largest Cartesian \( z\)-coordinate in c.
 
Kernel::FT min_coord (int i) const
 returns i-th Cartesian coordinate of the smallest vertex of c. More...
 
Kernel::FT max_coord (int i) const
 returns i-th Cartesian coordinate of the largest vertex of c. More...
 

Predicates

bool is_degenerate () const
 c is degenerate, if all vertices are coplanar.
 
Bounded_side bounded_side (const Point_3< Kernel > &p) const
 returns either ON_UNBOUNDED_SIDE, ON_BOUNDED_SIDE, or the constant ON_BOUNDARY, depending on where point p is.
 
bool has_on_boundary (const Point_3< Kernel > &p) const
 
bool has_on_bounded_side (const Point_3< Kernel > &p) const
 
bool has_on_unbounded_side (const Point_3< Kernel > &p) const
 

Miscellaneous

Kernel::FT volume () const
 returns the volume of c.
 
Bbox_3 bbox () const
 returns a bounding box containing c.
 
Iso_cuboid_3< Kernel > transform (const Aff_transformation_3< Kernel > &t) const
 returns the iso-oriented cuboid obtained by applying t on the smallest and the largest of c. More...
 

Constructor & Destructor Documentation

template<typename Kernel >
CGAL::Iso_cuboid_3< Kernel >::Iso_cuboid_3 ( const Point_3< Kernel > &  p,
const Point_3< Kernel > &  q 
)

introduces an iso-oriented cuboid c with diagonal opposite vertices p and q.

Note that the object is brought in the canonical form.

template<typename Kernel >
CGAL::Iso_cuboid_3< Kernel >::Iso_cuboid_3 ( const Point_3< Kernel > &  p,
const Point_3< Kernel > &  q,
int   
)

introduces an iso-oriented cuboid c with diagonal opposite vertices p and q.

The int argument value is only used to distinguish the two overloaded functions.

Precondition
p.x()<=q.x(), p.y()<=q.y()and p.z()<=q.z().
template<typename Kernel >
CGAL::Iso_cuboid_3< Kernel >::Iso_cuboid_3 ( const Kernel::RT &  min_hx,
const Kernel::RT &  min_hy,
const Kernel::RT &  min_hz,
const Kernel::RT &  max_hx,
const Kernel::RT &  max_hy,
const Kernel::RT &  max_hz,
const Kernel::RT &  hw = RT(1) 
)

introduces an iso-oriented cuboid c with diagonal opposite vertices (min_hx/hw, min_hy/hw, min_hz/hw) and (max_hx/hw, max_hy/hw, max_hz/hw).

Precondition
hw \( \neq\) 0.

Member Function Documentation

template<typename Kernel >
Kernel::FT CGAL::Iso_cuboid_3< Kernel >::max_coord ( int  i) const

returns i-th Cartesian coordinate of the largest vertex of c.

Precondition
\( 0 \leq i \leq2\).
template<typename Kernel >
Kernel::FT CGAL::Iso_cuboid_3< Kernel >::min_coord ( int  i) const

returns i-th Cartesian coordinate of the smallest vertex of c.

Precondition
\( 0 \leq i \leq2\).
template<typename Kernel >
Point_3<Kernel> CGAL::Iso_cuboid_3< Kernel >::operator[] ( int  i) const

returns vertex(i), as indicated in the figure below:

IsoCuboid.png
template<typename Kernel >
Iso_cuboid_3<Kernel> CGAL::Iso_cuboid_3< Kernel >::transform ( const Aff_transformation_3< Kernel > &  t) const

returns the iso-oriented cuboid obtained by applying t on the smallest and the largest of c.

Precondition
The angle at a rotation must be a multiple of \( \pi/2\), otherwise the resulting cuboid does not have the same size. Note that rotating about an arbitrary angle can even result in a degenerate iso-oriented cuboid.
template<typename Kernel >
Point_3<Kernel> CGAL::Iso_cuboid_3< Kernel >::vertex ( int  i) const

returns the i'th vertex modulo 8 of c.

starting with the lower left vertex.