- Authors
- Christophe Delage and Olivier Devillers
Introduction
Many geometric algorithms implemented in CGAL are incremental, and thus their speed is dependent on the order of insertion. This package provides sorting algorithms that may considerably improve running times of such algorithms.
The rationale is to sort objects along a space-filling curve so that two objects close geometrically will be close in the insertion order with high probability. That way, parts of a data structure that will be looked at during an insertion will probably have been looked at in a recent insertion, and thus probably will be in cache memory instead of main memory. As another side-effect, these sorting functions usually improve memory locality of the data structures produced by incremental algorithms, sometimes leading to speed ups in other algorithm using these data structures.
Some algorithms have a good complexity under randomized hypotheses which contradicts the idea of sorting the input using any sorting criterion. In such a case, it is possible to introduce just a bit of randomness to be able to combine the good randomized complexity and the good effects of locality [1].
The predicates used by this package are comparisons between coordinates, thus there is no robustness issue involved here, for example to choose the arithmetic of the kernel.
Hilbert Sorting
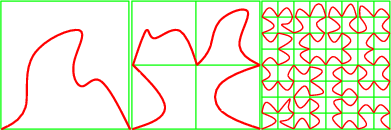
In 2D, one can construct a space filling curve, that is a mapping \( f\) of \( [0,1]\) to the unit square \( [0,1]^2\), such that \( f(0)=(0,0)\) and \( f(1)=(1,0)\) in the following way: the unit square is subdivided in four such that
\( f([0,\frac{1}{4}])=[0,\frac{1}{2}]^2\), \( f([\frac{1}{4},\frac{1}{2}])=[0,\frac{1}{2}]\times[\frac{1}{2},1]\), \( f([\frac{1}{2},\frac{3}{4}])=[\frac{1}{2},1]^2\), and \( f([\frac{3}{4},1])=[\frac{1}{2},1]\times[0,\frac{1}{2}].\)
\( f(\frac{1}{4})=(0,\frac{1}{2})\)
\( f(\frac{1}{2})=(\frac{1}{2},\frac{1}{2})\), and \( f(\frac{3}{4})=(1,\frac{1}{2})\).
Then each square is subdivided in the same way recursively. Figure 69.1 illustrates this process.
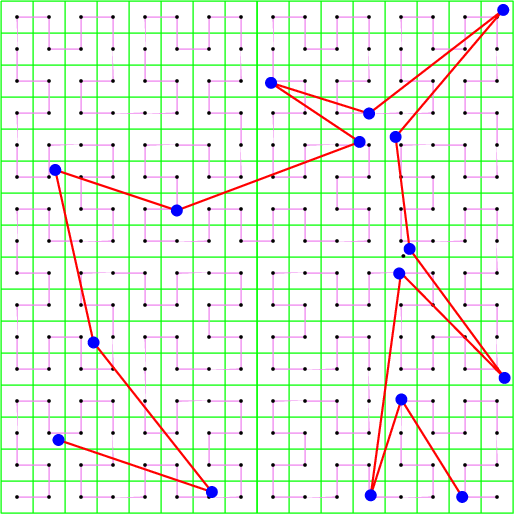
Now given a set of 2D points, they can be sorted in the order they have on such a space filling curve as illustrated in Figure 69.2 :
Examples
The code to use Hilbert sort is as simple as the following example:
File Spatial_sorting/hilbert.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/hilbert_sort.h>
#include <iostream>
#include <vector>
typedef K::Point_2 Point;
int main ()
{
std::size_t size = 16;
std::vector<Point> v; v.reserve(size);
CGAL::points_on_square_grid_2(3.0, size,
std::back_inserter(v), Creator());
for(std::size_t i=0; i<size; ++i)std::cout<<v[i]<<std::endl;
return 0;
}
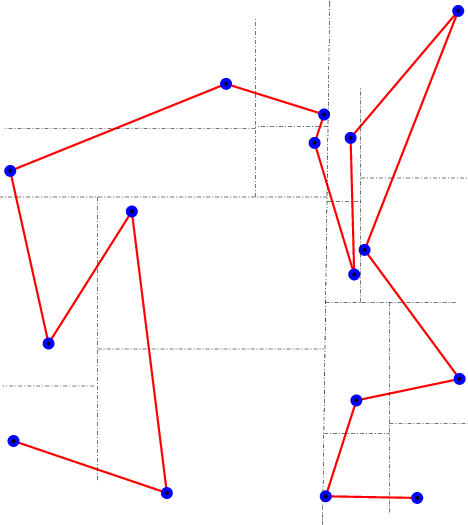
If instead of subdividing the square in a fixed way at its middle point, as above, we subdivide it by splitting at the median point (in \( x\) or \( y\) directions alternating), we construct a 2-d tree adapted to the point set. This tree can be visited in a similar manner and we get also a suitable ordering of the points (see Figure 69.3).
CGAL provides Hilbert sorting for points in 2D, 3D and higher dimensions, in the middle and the median policies.
The middle policy is easier to analyze, and is interesting in practice for well distributed set of points in small dimension (if the number of points is really smaller than \( 2^d\)). The median policy should be prefered for high dimension or if the point set distribution is not regular (or unknown). Since the median policy cannot be much worse than the middle policy, while the converse can happen, the median policy is the default behavior. Most theoretical results are using the middle policy [1], [3], [2],pb-scpts-89.
This other example illustrates the use of the two different policies
File Spatial_sorting/hilbert_policies.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/hilbert_sort.h>
#include <iostream>
#include <vector>
typedef K::Point_2 Point;
int main ()
{
std::vector<Point> v; v.reserve(4);
v.push_back( Point(0.0,0.0)) ;
v.push_back( Point(1.0,1.0)) ;
v.push_back( Point(0.1,0.1)) ;
v.push_back( Point(0.2,0.8)) ;
std::cout << "Hilbert sort (middle policy)." << std::endl;
std::cout<<v[0]<<"; "<<v[1]<<"; "<<v[2]<<"; "<<v[3]<<"; "<<std::endl;
std::cout << "Hilbert sort (median policy)." << std::endl;
std::cout<<v[0]<<"; "<<v[1]<<"; "<<v[2]<<"; "<<v[3]<<"; "<<std::endl;
return 0;
}
Spatial Sorting
Hilbert sort cannot be used directly before feeding a randomized algorithm. Thus, the trick is to organize the point set in random buckets of increasing sizes, Hilbert sort being used only inside a bucket.
It has been proved, in the context of Delaunay triangulation, that such an order provides enough randomness to combine the advantages of a random order and a space filling curve order [1].
CGAL provides spatial sorting for points in 2D, 3D and higher dimensions, with the middle and the median policies for Hilbert sort in the buckets.
Basic Example
The following example shows that, on particular input, spatial sort runs much faster than a bad order or than Hilbert sort (below results with release mode compilation on a 1.8GHz processor).
$ ./small_example_delaunay_2
10000 points on a parabola
Delaunay without spatial sort... done in 6.33443 seconds.
Delaunay with median hilbert sort... done in 0.822975 seconds.
Delaunay with median spatial sort... done in 0.022415 seconds.
File Spatial_sorting/small_example_delaunay_2.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/spatial_sort.h>
#include <CGAL/Timer.h>
#include <iostream>
#include <vector>
typedef CGAL::Delaunay_triangulation_2<K> DT;
void compute_delaunay(std::vector<K::Point_2>::iterator it,
std::vector<K::Point_2>::iterator e){
DT dt;
DT::Face_handle hint;
for( ;it!=e; ++it) hint = dt.insert(*it, hint)->face();
}
int main ()
{ int size = 1000;
std::vector<K::Point_2> v;
v.reserve(size);
CGAL::Timer cost;
std::cout <<size<< " points on a parabola" << std::endl;
for (int i=0; i< size; ++i) {
double x= -size +i;
v.push_back( K::Point_2( x, x*x ));
}
cost.reset();cost.start();
std::cout << " Delaunay without spatial sort... "<< std::flush;
compute_delaunay(v.begin(),v.end());cost.stop();
std::cout << "done in "<<cost.time()<<" seconds." << std::endl;
cost.reset();cost.start();
std::cout << " Delaunay with Hilbert sort... " << std::flush;
compute_delaunay(v.begin(),v.end());cost.stop();
std::cout << "done in "<<cost.time()<<" seconds." << std::endl;
cost.reset();cost.start();
std::cout << " Delaunay with spatial sort... " << std::flush;
compute_delaunay(v.begin(),v.end());cost.stop();
std::cout << "done in "<<cost.time()<<" seconds." << std::endl;
return 0;
}
Using Your Own Point Type
If you want to sort points of your own point type, you only have to provide functors that compare the x and y coordinates of your points. Note that in case you simply want to associate an extra information to your point you might consider the example of Section Sorting Using Pairs of Points and Integers as an alternative.
File Spatial_sorting/myPoint.cpp
#include <CGAL/spatial_sort.h>
struct MyPoint {
double x,y;
int color;
MyPoint()
: x(0), y(0),color(0)
{}
MyPoint(double x, double y, int color=0)
: x(x), y(y), color(color)
{}
};
struct MyLessX {
bool operator()(const MyPoint& p, const MyPoint& q) const
{
return p.x < q.x;
}
};
struct MyLessY {
bool operator()(const MyPoint& p, const MyPoint& q) const
{
return p.y < q.y;
}
};
struct MySpatialSortingTraits {
typedef MyPoint Point_2;
typedef MyLessX Less_x_2;
typedef MyLessY Less_y_2;
Less_x_2 less_x_2_object() const
{
return Less_x_2();
}
Less_y_2 less_y_2_object() const
{
return Less_y_2();
}
};
int main()
{
std::vector< MyPoint > points;
points.push_back(MyPoint(14,12, 3));
points.push_back(MyPoint(1,2 , 0));
points.push_back(MyPoint(414,2, 5));
points.push_back(MyPoint(4,21 , 1));
points.push_back(MyPoint(7,74 , 2));
points.push_back(MyPoint(74,4 , 4));
MySpatialSortingTraits sst;
for (std::vector< MyPoint >::iterator it=points.begin();it!=points.end();++it)
std::cout << it->color << " ";
std::cout << "\n";
std::cerr << "done" << std::endl;
return 0;
}
Sorting Arbitrary Types
The spatial sorting traits class provides a point type and functors for comparing, for example, the x-coordinates of two points. If you want to sort something else than just points, for example a sequence of tuples containing a point, or a sequence of indices in a vector of points, you need another level of indirection. We provide the spatial sorting traits class adapters which are templated by another spatial sorting traits class, and a property map. which allows to obtain a point from whatever you want to sort.
The following examples illustrate the usage of these traits class adapters.
Sorting Using Pairs of Points and Integers
In this example program, the sorted sequence of points is retrieved using a vector of pairs of points and integers.
File Spatial_sorting/sp_sort_using_property_map_2.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/spatial_sort.h>
#include <CGAL/Spatial_sort_traits_adapter_2.h>
#include <CGAL/property_map.h>
#include <vector>
typedef std::pair<Point_2,int> Point_with_info;
typedef std::vector< Point_with_info > Data_vector;
CGAL::First_of_pair_property_map<Point_with_info>
> Search_traits_2;
int main()
{
Data_vector points;
points.push_back(std::make_pair(Point_2(14,12) , 3));
points.push_back(std::make_pair(Point_2(1,2) , 0));
points.push_back(std::make_pair(Point_2(414,2) , 5));
points.push_back(std::make_pair(Point_2(4,21) , 1));
points.push_back(std::make_pair(Point_2(7,74) , 2));
points.push_back(std::make_pair(Point_2(74,4) , 4));
Search_traits_2 traits;
for (Data_vector::iterator it=points.begin();it!=points.end();++it)
std::cout << it->second << " ";
std::cout << "\n";
std::cout << "done" << std::endl;
return 0;
}
Sorting Using Indices of Points
In this example program, the sorted sequence of points is retrieved using the indices of the points in a vector of points.
File Spatial_sorting/sp_sort_using_property_map_3.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/spatial_sort.h>
#include <CGAL/Spatial_sort_traits_adapter_3.h>
#include <vector>
#include <boost/iterator/counting_iterator.hpp>
typedef
int main()
{
std::vector<Point_3> points;
points.push_back(Point_3(1,3,11));
points.push_back(Point_3(14,34,46));
points.push_back(Point_3(414,34,4));
points.push_back(Point_3(4,2,56));
points.push_back(Point_3(744,4154,43));
points.push_back(Point_3(74,44,1));
std::vector<std::ptrdiff_t> indices;
indices.reserve(points.size());
std::copy(boost::counting_iterator<std::ptrdiff_t>(0),
boost::counting_iterator<std::ptrdiff_t>(points.size()),
std::back_inserter(indices));
for (std::vector<std::ptrdiff_t>::iterator it=indices.begin();it!=indices.end();++it)
std::cout << points[*it] << "\n";
std::cout << "done" << std::endl;
return 0;
}
Sorting Using Indices of Pairs of Points and Integers
In this example program, the sorted sequence of points is retrieved using the indices of the points in a vector of pairs of points and integers.
File Spatial_sorting/sp_sort_using_property_map_d.cpp
#include <CGAL/Cartesian_d.h>
#include <CGAL/spatial_sort.h>
#include <CGAL/Spatial_sort_traits_adapter_d.h>
#include <boost/iterator/counting_iterator.hpp>
#include <vector>
typedef CGAL::Cartesian_d<double> Kernel;
typedef Kernel::Point_d Point_d;
typedef std::pair<Point_d,int> Point_with_info;
typedef std::vector< Point_with_info > Data_vector;
class Vect_ppmap{
const Data_vector& points;
public:
typedef Data_vector::size_type key_type;
typedef Point_d value_type;
typedef const value_type& reference;
typedef boost::readable_property_map_tag category;
Vect_ppmap(const Data_vector& points_):points(points_){}
friend reference get(const Vect_ppmap& vmap, key_type i) {
return vmap.points[i].first;
}
};
int main()
{
double coords[] ={ 1.0, 1.0, 1.0, 1.0,
2.0, 2.0, 2.0, 2.0 };
Data_vector points;
points.push_back(std::make_pair(Point_d(4,coords ,coords+4) , 1));
points.push_back(std::make_pair(Point_d(4,coords+4,coords+8) , 2));
std::vector<Vect_ppmap::key_type> indices;
indices.reserve(points.size());
std::copy(
boost::counting_iterator<Vect_ppmap::key_type>(0),
boost::counting_iterator<Vect_ppmap::key_type>(points.size()),
std::back_inserter(indices) );
indices.begin(),
indices.end(),
Search_traits_d(Vect_ppmap(points)) );
std::vector<Vect_ppmap::key_type>::iterator it=indices.begin();
for (;it!=indices.end();++it)
std::cout << points[*it].second << " ";
std::cout << std::endl;
std::cout << "done" << std::endl;
return 0;
}