|
CGAL 4.7 - 3D Polyhedral Surface
|
|
CGAL 4.7 - 3D Polyhedral Surface
|
#include <CGAL/Polyhedron_3.h>
A polyhedral surface Polyhedron_3 consists of vertices V, edges E, facets F and an incidence relation on them.
Each edge is represented by two halfedges with opposite orientations.
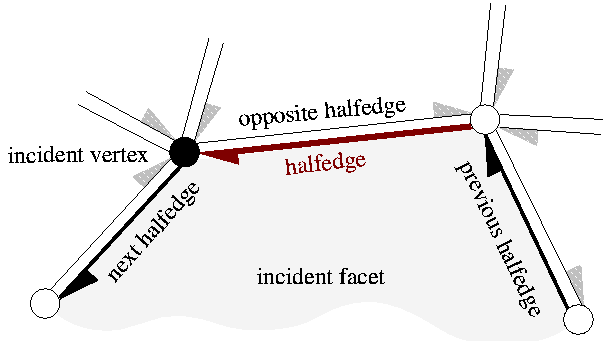
Vertices represent points in 3d-space. Edges are straight line segments between two endpoints. Facets are planar polygons without holes defined by the circular sequence of halfedges along their boundary. The polyhedral surface itself can have holes. The halfedges along the boundary of a hole are called border halfedges and have no incident facet. An edge is a border edge if one of its halfedges is a border halfedge. A surface is closed if it contains no border halfedges. A closed surface is a boundary representation for polyhedra in three dimensions. The convention is that the halfedges are oriented counterclockwise around facets as seen from the outside of the polyhedron. An implication is that the halfedges are oriented clockwise around the vertices. The notion of the solid side of a facet as defined by the halfedge orientation extends to polyhedral surfaces with border edges although they do not define a closed object. If normal vectors are considered for the facets, normals point outwards (following the right hand rule).
The strict definition can be found in [3]. One implication of this definition is that the polyhedral surface is always an orientable and oriented 2-manifold with border edges, i.e., the neighborhood of each point on the polyhedral surface is either homeomorphic to a disc or to a half disc, except for vertices where many holes and surfaces with boundary can join. Another implication is that the smallest representable surface is a triangle (for polyhedral surfaces with border edges) or a tetrahedron (for polyhedra). Boundary representations of orientable 2-manifolds are closed under Euler operations. They are extended with operations that create or close holes in the surface.
Other intersections besides the incidence relation are not allowed, although they are not automatically handled, since self intersections are not easy to check efficiently. Polyhedron_3 does only maintain the combinatorial integrity of the polyhedral surface (using Euler operations) and does not consider the coordinates of the points or any geometric information.
The class Polyhedron_3 can represent polyhedral surfaces as well as polyhedra. The interface is designed in such a way that it is easy to ignore border edges and work only with polyhedra.
The sequence of edges can be ordered in the data structure on request such that the sequence starts with the non-border edges and ends with the border edges. Border edges are then itself ordered such that the halfedge which is incident to the facet comes first and the halfedge incident to the hole comes thereafter. This normalization step counts simultaneously the number of border edges. This number is zero if and only if the surface is a closed polyhedron. Note that this class does not maintain this counter nor the halfedge order during further modifications. There is no automatic caching done for auxiliary information.
Parameters
The full template declaration of Polyhedron_3 states four template parameters:
The first parameter requires a model of the PolyhedronTraits_3 concept as argument, for example CGAL::Polyhedron_traits_3. The second parameter expects a model of the PolyhedronItems_3 concept. By default, the class CGAL::Polyhedron_items_3 is preselected. The third parameter is a class template. A model of the HalfedgeDS concept is expected. By default, the class CGAL::HalfedgeDS_default is preselected, which is a list based implementation of the halfedge data structure. The fourth parameter Alloc requires a standard allocator for STL container classes. The rebind mechanism from Alloc will be used to create appropriate allocators internally. A default is provided with the macro CGAL_ALLOCATOR(int) from the <CGAL/memory.h> header file.
CGAL::Polyhedron_3::Vertex CGAL::Polyhedron_3::Halfedge CGAL::Polyhedron_3::Facet PolyhedronTraits_3 CGAL::Polyhedron_traits_3<Kernel> PolyhedronItems_3 CGAL::Polyhedron_items_3 HalfedgeDS CGAL::HalfedgeDS_default CGAL::Polyhedron_incremental_builder_3<HDS> CGAL::Modifier_base.Example
This example program instantiates a polyhedron using the default traits class and creates a tetrahedron.
File Polyhedron/polyhedron_prog_simple.cpp
Classes | |
| class | Facet |
| A facet optionally stores a plane equation, and a reference to an incident halfedge that points to the facet. More... | |
| class | Halfedge |
| A halfedge is an oriented edge between two vertices. More... | |
| class | Vertex |
| A vertex optionally stores a point and a reference to an incident halfedge that points to the vertex. More... | |
Related Functions | |
(Note that these are not member functions.) | |
| template<class PolyhedronTraits_3 > | |
| std::istream & | operator>> (std::istream &in, CGAL::Polyhedron_3< PolyhedronTraits_3 > &P) |
| template<class PolyhedronTraits_3 > | |
| std::ostream & | operator<< (std::ostream &out, CGAL::Polyhedron_3< PolyhedronTraits_3 > &P) |
Types | |
| typedef unspecified_type | Items |
items class selected for PolyhedronItems_3. | |
| typedef unspecified_type | HalfedgeDS |
| instantiated halfedge data structure. | |
| typedef unspecified_type | size_type |
size type of HalfedgeDS. | |
| typedef unspecified_type | difference_type |
difference type of HalfedgeDS. | |
| typedef unspecified_type | iterator_category |
iterator category of HalfedgeDS for all iterators. | |
| typedef unspecified_type | circulator_category |
circulator category of all circulators; bidirectional category if the Items::Halfedge provides a Halfedge::prev() member function, otherwise forward category. | |
| typedef unspecified_type | allocator_type |
allocator type Alloc. | |
Handles, Iterators, and Circulators | |
The following handles, iterators, and circulators have appropriate non-mutable counterparts, i.e., The mutable types are assignable to their non-mutable counterparts. Both circulators are assignable to the All handles are model of | |
| typedef unspecified_type | Point_3 |
| point stored in vertices. | |
| typedef unspecified_type | Plane_3 |
| plane equation stored in facets (if supported). | |
| typedef unspecified_type | Vertex_handle |
| handle to vertex. | |
| typedef unspecified_type | Halfedge_handle |
| handle to halfedge. | |
| typedef unspecified_type | Facet_handle |
| handle to facet. | |
| typedef unspecified_type | Vertex_iterator |
| iterator over all vertices. | |
| typedef unspecified_type | Halfedge_iterator |
| iterator over all halfedges. | |
| typedef unspecified_type | Facet_iterator |
| iterator over all facets. | |
| typedef unspecified_type | Halfedge_around_vertex_circulator |
| circulator of halfedges around a vertex (cw). | |
| typedef unspecified_type | Halfedge_around_facet_circulator |
| circulator of halfedges around a facet (ccw). | |
| typedef unspecified_type | Edge_iterator |
| iterator over all edges (every other halfedge). | |
| typedef unspecified_type | Point_iterator |
| iterator over all points. | |
| typedef unspecified_type | Plane_iterator |
| iterator over all plane equations. | |
Types for Tagging Optional Features | |
The following types are equal to either | |
| typedef unspecified_type | Supports_vertex_halfedge |
Vertex::halfedge(). | |
| typedef unspecified_type | Supports_vertex_point |
Vertex::point(). | |
| typedef unspecified_type | Supports_halfedge_prev |
Halfedge::prev(). | |
| typedef unspecified_type | Supports_halfedge_vertex |
Halfedge::vertex(). | |
| typedef unspecified_type | Supports_halfedge_facet |
Halfedge::facet(). | |
| typedef unspecified_type | Supports_facet_halfedge |
Facet::halfedge(). | |
| typedef unspecified_type | Supports_facet_plane |
Facet::plane(). | |
| typedef unspecified_type | Supports_removal |
| supports removal of individual elements. | |
Creation | |
| Polyhedron_3 (const Traits &traits=Traits()) | |
| Default constructor. | |
| Polyhedron_3 (size_type v, size_type h, size_type f, const Traits &traits=Traits()) | |
Cosntructor of a polyhedron with storage reserved for v vertices, h halfedges, and f facets. More... | |
| void | reserve (size_type v, size_type h, size_type f) |
reserve storage for v vertices, h halfedges, and f facets. More... | |
| Halfedge_handle | make_tetrahedron () |
| a tetrahedron is added to the polyhedral surface. More... | |
| Halfedge_handle | make_tetrahedron (const Point &p1, const Point &p2, const Point &p3, const Point &p4) |
a tetrahedron is added to the polyhedral surface with its vertices initialized to p1, p2, p3, and p4. More... | |
| Halfedge_handle | make_triangle () |
| a triangle with border edges is added to the polyhedral surface. More... | |
| Halfedge_handle | make_triangle (const Point &p1, const Point &p2, const Point &p3) |
a triangle with border edges is added to the polyhedral surface with its vertices initialized to p1, p2, and p3. More... | |
Access Member Functions | |
| bool | empty () const |
| returns true if the polyhedron is empty. | |
| size_type | size_of_vertices () const |
| number of vertices. | |
| size_type | size_of_halfedges () const |
| number of halfedges (incl. border halfedges). | |
| size_type | size_of_facets () const |
| number of facets. | |
| size_type | capacity_of_vertices () const |
| space reserved for vertices. | |
| size_type | capacity_of_halfedges () const |
| space reserved for halfedges. | |
| size_type | capacity_of_facets () const |
| space reserved for facets. | |
| size_t | bytes () const |
| bytes used for the polyhedron. | |
| size_t | bytes_reserved () const |
| bytes reserved for the polyhedron. | |
| allocator_type | get_allocator () const |
| allocator object. | |
| Vertex_iterator | vertices_begin () |
| iterator over all vertices. | |
| Vertex_iterator | vertices_end () |
| past-the-end iterator. | |
| Halfedge_iterator | halfedges_begin () |
| iterator over all halfedges. | |
| Halfedge_iterator | halfedges_end () |
| past-the-end iterator. | |
| Facet_iterator | facets_begin () |
| iterator over all facets (excluding holes). | |
| Facet_iterator | facets_end () |
| past-the-end iterator. | |
| Edge_iterator | edges_begin () |
| iterator over all edges. | |
| Edge_iterator | edges_end () |
| past-the-end iterator. | |
| Point_iterator | points_begin () |
| iterator over all points. | |
| Point_iterator | points_end () |
| past-the-end iterator. | |
| Plane_iterator | planes_begin () |
| iterator over all plane equations. | |
| Plane_iterator | planes_end () |
| past-the-end iterator. | |
| const Traits & | traits () const |
| returns the traits class. | |
Combinatorial Predicates | |
| bool | is_closed () const |
returns true if there are no border edges. | |
| bool | is_pure_bivalent () const |
returns true if all vertices have exactly two incident edges. | |
| bool | is_pure_trivalent () const |
returns true if all vertices have exactly three incident edges. | |
| bool | is_pure_triangle () const |
returns true if all facets are triangles. | |
| bool | is_pure_quad () const |
returns true if all facets are quadrilaterals. | |
| bool | is_triangle (Halfedge_const_handle h) const |
true iff the connected component denoted by h is a triangle. | |
| bool | is_tetrahedron (Halfedge_const_handle h) const |
true iff the connected component denoted by h is a tetrahedron. | |
Euler Operators (Combinatorial Modifications) | |
|
The following Euler operations modify consistently the combinatorial structure of the polyhedral surface. The geometry remains unchanged. | |
| Halfedge_handle | split_facet (Halfedge_handle h, Halfedge_handle g) |
splits the facet incident to h and g into two facets with a new diagonal between the two vertices denoted by h and g respectively. More... | |
| Halfedge_handle | join_facet (Halfedge_handle h) |
joins the two facets incident to h. More... | |
| Halfedge_handle | split_vertex (Halfedge_handle h, Halfedge_handle g) |
splits the vertex incident to h and g into two vertices, the old vertex remains and a new copy is created, and connects them with a new edge. More... | |
| Halfedge_handle | join_vertex (Halfedge_handle h) |
joins the two vertices incident to h. More... | |
| Halfedge_handle | split_edge (Halfedge_handle h) |
splits the halfedge h into two halfedges inserting a new vertex that is a copy of h->opposite()->vertex(). More... | |
| Halfedge_handle | flip_edge (Halfedge_handle h) |
| performs an edge flip. More... | |
| Halfedge_handle | create_center_vertex (Halfedge_handle h) |
barycentric triangulation of h->facet(). More... | |
| Halfedge_handle | erase_center_vertex (Halfedge_handle g) |
reverses create_center_vertex(). More... | |
Euler Operators Modifying Genus | |
| Halfedge_handle | split_loop (Halfedge_handle h, Halfedge_handle i, Halfedge_handle j) |
cuts the polyhedron into two parts along the cycle (h,i,j) (edge j runs on the backside of the three dimensional figure above). More... | |
| Halfedge_handle | join_loop (Halfedge_handle h, Halfedge_handle g) |
glues the boundary of the two facets denoted by h and g together and returns h. More... | |
Modifying Facets and Holes | |
| Halfedge_handle | make_hole (Halfedge_handle h) |
removes the incident facet of h and changes all halfedges incident to the facet into border edges. More... | |
| Halfedge_handle | fill_hole (Halfedge_handle h) |
| fills a hole with a newly created facet. More... | |
| Halfedge_handle | add_vertex_and_facet_to_border (Halfedge_handle h, Halfedge_handle g) |
creates a new facet within the hole incident to h and g by connecting the tip of g with the tip of h with two new halfedges and a new vertex and filling this separated part of the hole with a new facet, such that the new facet is incident to g. More... | |
| Halfedge_handle | add_facet_to_border (Halfedge_handle h, Halfedge_handle g) |
creates a new facet within the hole incident to h and g by connecting the vertex denoted by g with the vertex denoted by h with a new halfedge and filling this separated part of the hole with a new facet, such that the new facet is incident to g. More... | |
Erasing | |
| void | erase_facet (Halfedge_handle h) |
removes the incident facet of h and changes all halfedges incident to the facet into border edges or removes them from the polyhedral surface if they were already border edges. More... | |
| void | erase_connected_component (Halfedge_handle h) |
removes the vertices, halfedges, and facets that belong to the connected component of h. More... | |
| unsigned int | keep_largest_connected_components (unsigned int nb_components_to_keep) |
| Erases the small connected components and the isolated vertices. More... | |
| void | clear () |
| removes all vertices, halfedges, and facets. | |
Operations with Border Halfedges | |
Advanced Halfedges incident to a hole are called border halfedges. An halfedge is a border edge if itself or its opposite halfedge are border halfedges. The only requirement to work with border halfedges is that the | |
| void | normalize_border () |
| sorts halfedges such that the non-border edges precede the border edges. More... | |
| size_type | size_of_border_halfedges () const |
| number of border halfedges. More... | |
| size_type | size_of_border_edges () const |
| number of border edges. More... | |
| Halfedge_iterator | border_halfedges_begin () |
| halfedge iterator starting with the border edges. More... | |
| Edge_iterator | border_edges_begin () |
| edge iterator starting with the border edges. More... | |
Miscellaneous | |
| void | inside_out () |
| reverses facet orientations (incl. plane equations if supported). | |
| bool | is_valid (bool verbose=false, int level=0) const |
returns true if the polyhedral surface is combinatorially consistent. More... | |
| bool | normalized_border_is_valid (bool verbose=false) const |
returns true if the border halfedges are in normalized representation, which is when enumerating all halfedges with the iterator: The non-border edges precede the border edges and for border edges, the second halfedge is the border halfedge. More... | |
| void | delegate (CGAL::Modifier_base< HDS > &m) |
| This is an advanced function. More... | |
| CGAL::Polyhedron_3< Traits >::Polyhedron_3 | ( | size_type | v, |
| size_type | h, | ||
| size_type | f, | ||
| const Traits & | traits = Traits() |
||
| ) |
Cosntructor of a polyhedron with storage reserved for v vertices, h halfedges, and f facets.
The reservation sizes are a hint for optimizing storage allocation.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::add_facet_to_border | ( | Halfedge_handle | h, |
| Halfedge_handle | g | ||
| ) |
creates a new facet within the hole incident to h and g by connecting the vertex denoted by g with the vertex denoted by h with a new halfedge and filling this separated part of the hole with a new facet, such that the new facet is incident to g.
Returns the halfedge of the new edge that is incident to the new facet.
h->is_border(), g->is_border(), h != g, h->next() != g, and g can be reached along the same hole starting with h.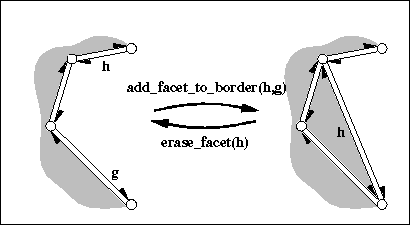
| Halfedge_handle CGAL::Polyhedron_3< Traits >::add_vertex_and_facet_to_border | ( | Halfedge_handle | h, |
| Halfedge_handle | g | ||
| ) |
creates a new facet within the hole incident to h and g by connecting the tip of g with the tip of h with two new halfedges and a new vertex and filling this separated part of the hole with a new facet, such that the new facet is incident to g.
Returns the halfedge of the new edge that is incident to the new facet and the new vertex.
h->is_border(), g->is_border(), h != g, and g can be reached along the same hole starting with h.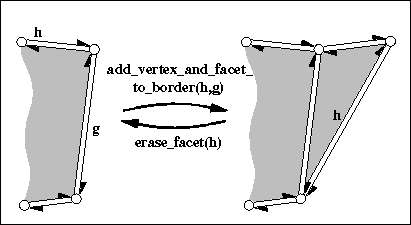
| Edge_iterator CGAL::Polyhedron_3< Traits >::border_edges_begin | ( | ) |
edge iterator starting with the border edges.
The range [edges_begin(), border_edges_begin()) denotes all non-border edges. The range [border_edges_begin(), edges_end()) denotes all border edges.
normalize_border() call still valid, see above. | Halfedge_iterator CGAL::Polyhedron_3< Traits >::border_halfedges_begin | ( | ) |
halfedge iterator starting with the border edges.
The range [halfedges_begin(), border_halfedges_begin()) denotes all non-border halfedges. The range [border_halfedges_begin(), halfedges_end()) denotes all border edges.
normalize_border() call still valid, see above. | Halfedge_handle CGAL::Polyhedron_3< Traits >::create_center_vertex | ( | Halfedge_handle | h) |
barycentric triangulation of h->facet().
Creates a new vertex, a copy of h->vertex(), and connects it to each vertex incident to h->facet() splitting h->facet() into triangles. h remains incident to the original facet, all other triangles are copies of this facet. Returns the halfedge h->next() after the operation, i.e., a halfedge pointing to the new vertex. The time is proportional to the size of the facet.
h is not a border halfedge.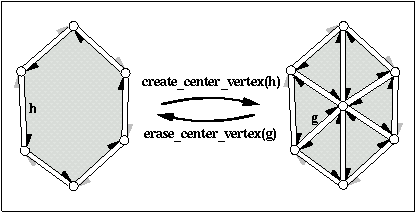
| void CGAL::Polyhedron_3< Traits >::delegate | ( | CGAL::Modifier_base< HDS > & | m) |
This is an advanced function.
calls the Modifier_base::operator()() of the modifier m.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::erase_center_vertex | ( | Halfedge_handle | g) |
reverses create_center_vertex().
Erases the vertex pointed to by g and all incident halfedges thereby merging all incident facets. Only g->facet() remains. The neighborhood of g->vertex() may not be triangulated, it can have larger facets. Returns the halfedge g->prev(). Thus, the invariant h == erase_center_vertex( create_center_vertex(h)) holds if h is not a border halfedge. The time is proportional to the sum of the size of all incident facets.
g->vertex() is a hole. There are at least two distinct facets incident to the facets that are incident to g->vertex(). (This prevents the operation from collapsing a volume into two facets glued together with opposite orientations, such as would happen with any vertex of a tetrahedron.)Supports_removal \( \equiv\) CGAL::Tag_true. 
| void CGAL::Polyhedron_3< Traits >::erase_connected_component | ( | Halfedge_handle | h) |
removes the vertices, halfedges, and facets that belong to the connected component of h.
Supports_removal \( \equiv\) CGAL::Tag_true. | void CGAL::Polyhedron_3< Traits >::erase_facet | ( | Halfedge_handle | h) |
removes the incident facet of h and changes all halfedges incident to the facet into border edges or removes them from the polyhedral surface if they were already border edges.
If this creates isolated vertices they get removed as well. See make_hole(h) for a more specialized variant.
h->is_border() == false.Supports_removal \( \equiv\) CGAL::Tag_true

| Halfedge_handle CGAL::Polyhedron_3< Traits >::fill_hole | ( | Halfedge_handle | h) |
fills a hole with a newly created facet.
Makes all border halfedges of the hole denoted by h incident to the new facet. Returns h.
h.is_border(). | Halfedge_handle CGAL::Polyhedron_3< Traits >::flip_edge | ( | Halfedge_handle | h) |
performs an edge flip.
It returns h after rotating the edge h one vertex in the direction of the face orientation.
h != Halfedge_handle() and both facets incident to h are triangles. | bool CGAL::Polyhedron_3< Traits >::is_valid | ( | bool | verbose = false, |
| int | level = 0 |
||
| ) | const |
returns true if the polyhedral surface is combinatorially consistent.
If verbose is true, statistics are printed to cerr. For level == 1 the normalization of the border edges is checked too. This method checks in particular level 3 of CGAL::Halfedge_data_structure_decorator::is_valid() from CGAL::HalfedgeDS_const_decorator and that each facet is at least a triangle and that the two incident facets of a non-border edge are distinct.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::join_facet | ( | Halfedge_handle | h) |
joins the two facets incident to h.
The facet incident to h->opposite() gets removed. Both facets might be holes. Returns the predecessor of h around the facet. The invariant join_facet( split_facet( h, g)) returns h and keeps the polyhedron unchanged. The time is proportional to the size of the facet removed and the time to compute h->prev().
h is at least three (no antennas).Supports_removal \( \equiv\) CGAL::Tag_true.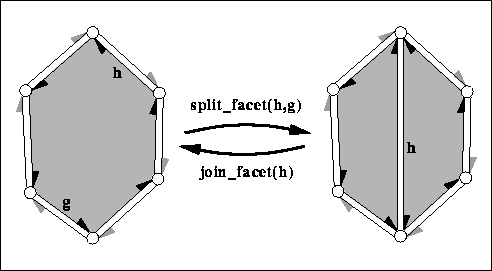
n
| Halfedge_handle CGAL::Polyhedron_3< Traits >::join_loop | ( | Halfedge_handle | h, |
| Halfedge_handle | g | ||
| ) |
glues the boundary of the two facets denoted by h and g together and returns h.
Both facets and the vertices along the facet denoted by g gets removed. Both facets may be holes. The invariant join_loop( h, split_loop( h, i, j)) returns h and keeps the polyhedron unchanged.
h and g are different and have equal degree (i.e., number of edges).Supports_removal \( \equiv\) CGAL::Tag_true. 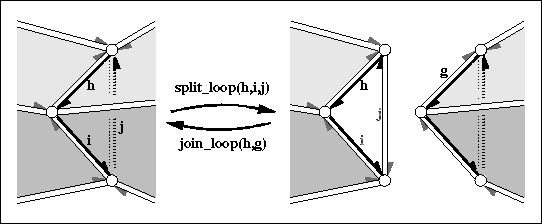
| Halfedge_handle CGAL::Polyhedron_3< Traits >::join_vertex | ( | Halfedge_handle | h) |
joins the two vertices incident to h.
The vertex denoted by h->opposite() gets removed. Returns the predecessor of h around the vertex, i.e., h->opposite()->prev(). The invariant join_vertex( split_vertex( h, g)) returns h and keeps the polyhedron unchanged. The time is proportional to the degree of the vertex removed and the time to compute h->prev() and h->opposite()->prev().
h is at least four (no multi-edges).Supports_removal \( \equiv\) CGAL::Tag_true. 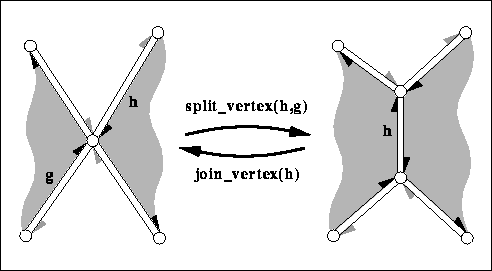
| unsigned int CGAL::Polyhedron_3< Traits >::keep_largest_connected_components | ( | unsigned int | nb_components_to_keep) |
Erases the small connected components and the isolated vertices.
Keep nb_components_to_keep largest connected components. Returns the number of connected components erased (ignoring isolated vertices).
| Halfedge_handle CGAL::Polyhedron_3< Traits >::make_hole | ( | Halfedge_handle | h) |
removes the incident facet of h and changes all halfedges incident to the facet into border edges.
Returns h. See erase_facet(h) for a more generalized variant.
Supports_removal \( \equiv\) CGAL::Tag_true. | Halfedge_handle CGAL::Polyhedron_3< Traits >::make_tetrahedron | ( | ) |
a tetrahedron is added to the polyhedral surface.
Returns a halfedge of the tetrahedron.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::make_tetrahedron | ( | const Point & | p1, |
| const Point & | p2, | ||
| const Point & | p3, | ||
| const Point & | p4 | ||
| ) |
a tetrahedron is added to the polyhedral surface with its vertices initialized to p1, p2, p3, and p4.
Returns that halfedge of the tetrahedron which incident vertex is initialized to p1. The incident vertex of the next halfedge is p2, and the vertex thereafter is p3. The remaining fourth vertex is initialized to p4.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::make_triangle | ( | ) |
a triangle with border edges is added to the polyhedral surface.
Returns a non-border halfedge of the triangle.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::make_triangle | ( | const Point & | p1, |
| const Point & | p2, | ||
| const Point & | p3 | ||
| ) |
a triangle with border edges is added to the polyhedral surface with its vertices initialized to p1, p2, and p3.
Returns that non-border halfedge of the triangle which incident vertex is initialized to p1. The incident vertex of the next halfedge is p2, and the vertex thereafter is p3.
| void CGAL::Polyhedron_3< Traits >::normalize_border | ( | ) |
sorts halfedges such that the non-border edges precede the border edges.
For each border edge the halfedge iterator will reference the halfedge incident to the facet right before the halfedge incident to the hole.
| bool CGAL::Polyhedron_3< Traits >::normalized_border_is_valid | ( | bool | verbose = false) | const |
returns true if the border halfedges are in normalized representation, which is when enumerating all halfedges with the iterator: The non-border edges precede the border edges and for border edges, the second halfedge is the border halfedge.
The halfedge iterator border_halfedges_begin() denotes the first border edge. If verbose is true, statistics are printed to cerr.
| void CGAL::Polyhedron_3< Traits >::reserve | ( | size_type | v, |
| size_type | h, | ||
| size_type | f | ||
| ) |
reserve storage for v vertices, h halfedges, and f facets.
The reservation sizes are a hint for optimizing storage allocation. If the capacity is already greater than the requested size nothing happens. If the capacity changes all iterators and circulators might invalidate.
| size_type CGAL::Polyhedron_3< Traits >::size_of_border_edges | ( | ) | const |
number of border edges.
Since each border edge of a polyhedral surface has exactly one border halfedge, this number is equal to size_of_border_halfedges().
normalize_border() call still valid, see above. | size_type CGAL::Polyhedron_3< Traits >::size_of_border_halfedges | ( | ) | const |
number of border halfedges.
normalize_border() call still valid, see above. | Halfedge_handle CGAL::Polyhedron_3< Traits >::split_edge | ( | Halfedge_handle | h) |
splits the halfedge h into two halfedges inserting a new vertex that is a copy of h->opposite()->vertex().
Is equivalent to split_vertex( h->prev(), h->opposite())->opposite(). The call of prev() can make this method slower than a direct call of split_vertex() if the previous halfedge is already known and computing it would be costly when the halfedge data structure does not support the prev() member function. Returns the new halfedge hnew pointing to the inserted vertex. The new halfedge is followed by the old halfedge, i.e., hnew->next() == h.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::split_facet | ( | Halfedge_handle | h, |
| Halfedge_handle | g | ||
| ) |
splits the facet incident to h and g into two facets with a new diagonal between the two vertices denoted by h and g respectively.
The second (new) facet is a copy of the first facet. Returns h->next() after the operation, i.e., the new diagonal. The new face is to the right of the new diagonal, the old face is to the left. The time is proportional to the distance from h to g around the facet.
h and g are incident to the same facet. h != g (no loops). h->next() != g and g->next() != h (no multi-edges).
| Halfedge_handle CGAL::Polyhedron_3< Traits >::split_loop | ( | Halfedge_handle | h, |
| Halfedge_handle | i, | ||
| Halfedge_handle | j | ||
| ) |
cuts the polyhedron into two parts along the cycle (h,i,j) (edge j runs on the backside of the three dimensional figure above).
Three new vertices (one copy for each vertex in the cycle) and three new halfedges (one copy for each halfedge in the cycle), and two new triangles are created. h,i,j will be incident to the first new triangle. The return value will be the halfedge incident to the second new triangle which is the copy of h-opposite().
h, i, j denote distinct, consecutive vertices of the polyhedron and form a cycle: i.e., h->vertex() == i->opposite()->vertex(), \( \ldots\) , j->vertex() == h->opposite()->vertex(). The six facets incident to (h,i,j) are all distinct.
| Halfedge_handle CGAL::Polyhedron_3< Traits >::split_vertex | ( | Halfedge_handle | h, |
| Halfedge_handle | g | ||
| ) |
splits the vertex incident to h and g into two vertices, the old vertex remains and a new copy is created, and connects them with a new edge.
Let hnew be h->next()->opposite() after the split, i.e., a halfedge of the new edge. The split regroups the halfedges around the two vertices. The halfedge sequence hnew, g->next()->opposite(), \( \ldots\) , h remains around the old vertex, while the halfedge sequence hnew->opposite(), h->next()->opposite() (before the split), \( \ldots\) , g is regrouped around the new vertex. The split returns hnew, i.e., the new halfedge incident to the old vertex. The time is proportional to the distance from h to g around the vertex.
h and g are incident to the same vertex. h != g (antennas are not allowed).
split_vertex(h,h->next()->opposite()) which is equivalent to an edge split of the halfedge h->next() that creates a new vertex on the halfedge h->next(). See also split_edge(h) below.