User Manual

Authors

Baruch Zukerman, Ron Wein, and Efi Fogel

Introduction

Let \( {\mathcal C} = \{C_1, C_2, \ldots, C_n\}\) be a set of curves. We wish to compute all intersection points between two curves in the set in an output-sensitive manner, without having to go over all \( O(n^2)\) curve pairs. To this end, we sweep an imaginary line \( l\) from \( x = -\infty\) to \( x = \infty\) over the plane. While sweeping the plane, we keep track of the order of curves intersecting it. This order changes at a finite number of event points, such that we only have to calculate the intersection points between two curves when they become contiguous. For more details on the sweep-line algorithm see, for example, [1], Chapter 2.

This chapter describes three functions implemented using the sweep-line algorithm: given a collection of input curves, compute all intersection points, compute the set of subcurves that are pairwise interior-disjoint induced by them, and checking whether there is at least one pair of curves among them that intersect in their interior.

The implementation is robust. It supports general curves and handles all degenerate cases, including overlapping curves, vertical segments, and tangency between curves. The robustness of the algorithm is guaranteed if the functions are instantiated with a traits class that employs certified computations. This traits class must be a model of the ArrangementTraits_2 concept - see the Chapter 2D Arrangements for more details.

The complexity of the sweep-line algorithm is \( O((n + k)\log{n})\) where \( n\) is the number of the input curves and \( k\) is the number of intersection points induced by these curves.

Example

The simple program listed below computes intersection points induced by a set of four input segments illustrated in Figure 33.1.

Figure 33.1 Four input segments

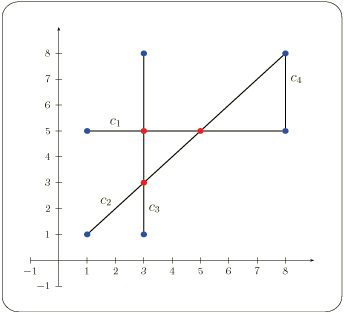
File Arrangement_on_surface_2/sweep_line.cpp

// Computing intersection points among curves using the sweep line.

#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Sweep_line_2_algorithms.h>
#include <list>

typedef CGAL::Quotient<CGAL::MP_Float>                  NT;
typedef CGAL::Cartesian<NT>                             Kernel;
typedef Kernel::Point_2                                 Point_2;
typedef CGAL::Arr_segment_traits_2<Kernel>              Traits_2;
typedef Traits_2::Curve_2                               Segment_2;

int main()
{
  // Construct the input segments.
  Segment_2 segments[] = {Segment_2 (Point_2 (1, 5), Point_2 (8, 5)),
                          Segment_2 (Point_2 (1, 1), Point_2 (8, 8)),
                          Segment_2 (Point_2 (3, 1), Point_2 (3, 8)),
                          Segment_2 (Point_2 (8, 5), Point_2 (8, 8))};
  
  // Compute all intersection points.
  std::list<Point_2>     pts;

  CGAL::compute_intersection_points (segments, segments + 4,
                                     std::back_inserter (pts));
  
  // Print the result.
  std::cout << "Found " << pts.size() << " intersection points: " << std::endl; 
  std::copy (pts.begin(), pts.end(),
             std::ostream_iterator<Point_2>(std::cout, "\n"));

  // Compute the non-intersecting sub-segments induced by the input segments.
  std::list<Segment_2>   sub_segs;

  CGAL::compute_subcurves(segments, segments + 4, std::back_inserter(sub_segs));

  std::cout << "Found " << sub_segs.size()
            << " interior-disjoint sub-segments." << std::endl;

  CGAL_assertion (CGAL::do_curves_intersect (segments, segments + 4));

  return 0;
}

Design and Implementation History

The current version of the sweep-line algorithm was written by Baruch Zukerman, based on previous implementations by Ester Ezra and Tali Zvi.