|
CGAL 4.7 - 3D Triangulations
|
|
CGAL 4.7 - 3D Triangulations
|
#include <CGAL/Regular_triangulation_3.h>
Let \( {S}^{(w)}\) be a set of weighted points in \( \mathbb{R}^3\).
Let \( {p}^{(w)}=(p,w_p), p\in\mathbb{R}^3, w_p\in\mathbb{R}\) and \( {z}^{(w)}=(z,w_z), z\in\mathbb{R}^3, w_z\in\mathbb{R}\) be two weighted points. A weighted point \( {p}^{(w)}=(p,w_p)\) can also be seen as a sphere of center \( p\) and radius \( \sqrt{w_p}\). The power product (or power distance ) between \( {p}^{(w)}\) and \( {z}^{(w)}\) is defined as
\[ \Pi({p}^{(w)},{z}^{(w)}) = {\|{p-z}\|^2-w_p-w_z} \]
where \( \|{p-z}\|\) is the Euclidean distance between \( p\) and \( z\). \( {p}^{(w)}\) and \( {z}^{(w)}\) are said to be orthogonal if \( \Pi{({p}^{(w)}-{z}^{(w)})} = 0\) (see Figure 40.2).
Four weighted points have a unique common orthogonal weighted point called the power sphere. A sphere \( {z}^{(w)}\) is said to be regular if \( \forall {p}^{(w)}\in{S}^{(w)}, \Pi{({p}^{(w)}-{z}^{(w)})}\geq 0\).
A triangulation of \( {S}^{(w)}\) is regular if the power spheres of all simplices are regular.
| RegularTriangulationTraits_3 | is the geometric traits class. |
| TriangulationDataStructure_3 | is the triangulation data structure. It has the default value Triangulation_data_structure_3<Triangulation_vertex_base_3<RegularTriangulationTraits_3>, Regular_triangulation_cell_base_3<RegularTriangulationTraits_3> >. |
| SurjectiveLockDataStructure | is an optional parameter to specify the type of the spatial lock data structure. It is only used if the triangulation data structure used is concurrency-safe (i.e. when TriangulationDataStructure_3::Concurrency_tag is Parallel_tag). It must be a model of the SurjectiveLockDataStructure concept, with Object being a Point. The default value is Spatial_lock_grid_3<Tag_priority_blocking> if the triangulation data structure is concurrency-safe, and void otherwise. In order to use concurrent operations, the user must provide a reference to a SurjectiveLockDataStructure instance via the constructor or Triangulation_3::set_lock_data_structure. |
If TriangulationDataStructure_3::Concurrency_tag is Parallel_tag, some operations, such as insertion/removal of a range of points, are performed in parallel. See the documentation of the operations for more details.
CGAL::Delaunay_triangulation_3 Types | |
|
typedef RegularTriangulationTraits_3::Bare_point | Bare_point |
The type for points p of weighted points \( {p}^{(w)}=(p,w_p)\). | |
|
typedef RegularTriangulationTraits_3::Weighted_point_3 | Weighted_point |
| typedef SurjectiveLockDataStructure | Lock_data_structure |
Creation | |
| Regular_triangulation_3 (const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3(), Lock_data_structure *lock_ds=NULL) | |
Creates an empty regular triangulation, possibly specifying a traits class traits. More... | |
| Regular_triangulation_3 (const Regular_triangulation_3 &rt1) | |
| Copy constructor. More... | |
| template<class InputIterator > | |
| Regular_triangulation_3 (InputIterator first, InputIterator last, const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3(), Lock_data_structure *lock_ds=NULL) | |
Equivalent to constructing an empty triangulation with the optional traits class argument and calling insert(first,last). More... | |
| template<class InputIterator > | |
| Regular_triangulation_3 (InputIterator first, InputIterator last, Lock_data_structure *lock_ds, const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3()) | |
| Same as before, with last two parameters in reverse order. | |
Insertion | |
The following methods, which already exist in The following method allows one to insert several points. | |
| Vertex_handle | insert (const Weighted_point &p, Cell_handle start=Cell_handle(), bool *could_lock_zone=NULL) |
Inserts weighted point p in the triangulation. More... | |
| Vertex_handle | insert (const Weighted_point &p, Vertex_handle hint, bool *could_lock_zone=NULL) |
Same as above but uses hint as a starting place for the search. | |
| Vertex_handle | insert (const Weighted_point &p, Locate_type lt, Cell_handle loc, int li, int lj, bool *could_lock_zone=NULL) |
Inserts weighted point p in the triangulation and returns the corresponding vertex. More... | |
| template<class InputIterator > | |
| std::ptrdiff_t | insert (InputIterator first, InputIterator last) |
Inserts the weighted points in the range [first,last). More... | |
| template<class WeightedPointWithInfoInputIterator > | |
| std::ptrdiff_t | insert (WeightedPointWithInfoInputIterator first, WeightedPointWithInfoInputIterator last) |
Inserts the weighted points in the iterator range [first,last). More... | |
The following methods, which already exist in | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (Weighted_point p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i) |
| Creates a new vertex by starring a hole. More... | |
| template<class CellIt > | |
| Vertex_handle | insert_in_hole (Weighted_point p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i, Vertex_handle newv) |
Same as above, except that newv will be used as the new vertex, which must have been allocated previously with, e.g. create_vertex. | |
Removal | |
| void | remove (Vertex_handle v) |
Removes the vertex v from the triangulation. | |
| bool | remove (Vertex_handle v, bool *could_lock_zone) |
Removes the vertex v from the triangulation. More... | |
| template<typename InputIterator > | |
| int | remove (InputIterator first, InputIterator beyond) |
Removes the vertices specified by the iterator range [first, beyond). More... | |
Queries | |
Let us remark that \( \Pi({p}^{(w)}-{z}^{(w)}) > 0 \) is equivalent to This remark helps provide an intuition about the following predicates. 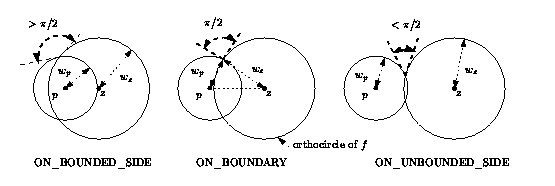
side_of_power_circle | |
| Bounded_side | side_of_power_sphere (Cell_handle c, const Weighted_point &p) const |
Returns the position of the weighted point \( p\) with respect to the power sphere of c. More... | |
| Bounded_side | side_of_power_circle (const Facet &f, const Weighted_point &p) const |
Returns the position of the point p with respect to the power circle of f. More... | |
| Bounded_side | side_of_power_circle (Cell_handle c, int i, const Weighted_point &p) const |
Same as the previous method for facet i of cell c. | |
| Bounded_side | side_of_power_segment (Cell_handle c, const Weighted_point &p) const |
| In dimension 1, returns. More... | |
| Vertex_handle | nearest_power_vertex (Weighted_point p, Cell_handle c=Cell_handle()) |
| Returns the vertex of the triangulation which is nearest to \( p\) with respect to the power distance. More... | |
| Vertex_handle | nearest_power_vertex_in_cell (Weighted_point p, Cell_handle c) |
Returns the vertex of the cell c that is nearest to \( p\) with respect to the power distance. | |
A weighted point | |
| template<class OutputIteratorBoundaryFacets , class OutputIteratorCells , class OutputIteratorInternalFacets > | |
| Triple < OutputIteratorBoundaryFacets, OutputIteratorCells, OutputIteratorInternalFacets > | find_conflicts (const Weighted_point p, Cell_handle c, OutputIteratorBoundaryFacets bfit, OutputIteratorCells cit, OutputIteratorInternalFacets ifit, bool *could_lock_zone=NULL, const Facet *this_facet_must_be_in_the_cz=NULL, bool *the_facet_is_in_its_cz=NULL) |
Compute the conflicts with p. More... | |
| template<class OutputIterator > | |
| OutputIterator | vertices_in_conflict (Weighted_point p, Cell_handle c, OutputIterator res) |
| template<class OutputIterator > | |
| OutputIterator | vertices_on_conflict_zone_boundary (Weighted_point p, Cell_handle c, OutputIterator res) |
Similar to find_conflicts(), but reports the vertices which are on the boundary of the conflict zone of p, in the output iterator res. More... | |
| template<class OutputIterator > | |
| OutputIterator | vertices_inside_conflict_zone (Weighted_point p, Cell_handle c, OutputIterator res) |
Similar to find_conflicts(), but reports the vertices which are in the interior of the conflict zone of p, in the output iterator res. More... | |
In the weighted setting, a face (cell, facet, edge or vertex) is said to be a Gabriel face iff the smallest sphere orthogonal to the weighted points associated to its vertices, has a positive power product with the weighted point of any other vertex of the triangulation. Any weighted Gabriel face belongs to the regular triangulation, but the reciprocal is not true. The following member functions test the Gabriel property of the faces of the regular triangulation. | |
| bool | is_Gabriel (Cell_handle c, int i) |
| bool | is_Gabriel (Cell_handle c, int i, int j) |
| bool | is_Gabriel (const Facet &f) |
| bool | is_Gabriel (const Edge &e) |
| bool | is_Gabriel (Vertex_handle v) |
Power Diagram | |
CGAL offers several functionalities to display the power diagram of a set of points in 3D. Note that the user should use a kernel with exact constructions in order to guarantee the computation of the Voronoi diagram (as opposed to computing the triangulation only, which requires only exact predicates). | |
| Bare_point | dual (Cell_handle c) const |
| Returns the weighted circumcenter of the four vertices of c. More... | |
| Object | dual (Facet f) const |
Returns the dual of facet f, which is. More... | |
| Object | dual (Cell_handle c, int i) const |
same as the previous method for facet (c,i). | |
| template<class Stream > | |
| Stream & | draw_dual (Stream &os) |
Sends the set of duals to all the facets of rt into os. | |
Checking | |
| bool | is_valid (bool verbose=false) const |
| This is a function for debugging purpose. More... | |
Additional Inherited Members | |
 Public Types inherited from CGAL::Triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure > Public Types inherited from CGAL::Triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure > | |
| enum | Locate_type |
The enum Locate_type is defined by Triangulation_3 to specify which case occurs when locating a point in the triangulation. | |
|
typedef TriangulationDataStructure_3 | Triangulation_data_structure |
| typedef SurjectiveLockDataStructure | Lock_data_structure |
|
typedef RegularTriangulationTraits_3 | Geom_traits |
|
typedef RegularTriangulationTraits_3::Point_3 | Point |
|
typedef RegularTriangulationTraits_3::Segment_3 | Segment |
|
typedef RegularTriangulationTraits_3::Triangle_3 | Triangle |
|
typedef RegularTriangulationTraits_3::Tetrahedron_3 | Tetrahedron |
|
typedef TriangulationDataStructure_3::Vertex | Vertex |
|
typedef TriangulationDataStructure_3::Cell | Cell |
|
typedef TriangulationDataStructure_3::Facet | Facet |
|
typedef TriangulationDataStructure_3::Edge | Edge |
|
typedef TriangulationDataStructure_3::Vertex_handle | Vertex_handle |
| handle to a vertex | |
|
typedef TriangulationDataStructure_3::Cell_handle | Cell_handle |
| handle to a cell | |
|
typedef Triangulation_simplex_3< Self > | Simplex |
| Reference to a simplex (vertex, edge, facet or cell) of the triangulation. | |
|
typedef TriangulationDataStructure_3::size_type | size_type |
| Size type (an unsigned integral type) | |
|
typedef TriangulationDataStructure_3::difference_type | difference_type |
| Difference type (a signed integral type) | |
|
typedef TriangulationDataStructure_3::Cell_iterator | All_cells_iterator |
| iterator over cells | |
|
typedef TriangulationDataStructure_3::Facet_iterator | All_facets_iterator |
| iterator over facets | |
|
typedef TriangulationDataStructure_3::Edge_iterator | All_edges_iterator |
| iterator over edges | |
|
typedef TriangulationDataStructure_3::Vertex_iterator | All_vertices_iterator |
| iterator over vertices | |
| typedef unspecified_type | Finite_cells_iterator |
| iterator over finite cells | |
| typedef unspecified_type | Finite_facets_iterator |
| iterator over finite facets | |
| typedef unspecified_type | Finite_edges_iterator |
| iterator over finite edges | |
| typedef unspecified_type | Finite_vertices_iterator |
| iterator over finite vertices | |
| typedef unspecified_type | Point_iterator |
| iterator over the points corresponding to the finite vertices of the triangulation. | |
|
typedef TriangulationDataStructure_3::Cell_circulator | Cell_circulator |
| circulator over all cells incident to a given edge | |
|
typedef TriangulationDataStructure_3::Facet_circulator | Facet_circulator |
| circulator over all facets incident to a given edge | |
|
typedef TriangulationDataStructure_3::Concurrency_tag | Concurrency_tag |
| Concurrency tag (from the TDS). | |
 Public Member Functions inherited from CGAL::Triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure > Public Member Functions inherited from CGAL::Triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure > | |
| Triangulation_3 (const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3(), Lock_data_structure *lock_ds=NULL) | |
Introduces a triangulation t having only one vertex which is the infinite vertex. More... | |
| Triangulation_3 (Lock_data_structure *lock_ds=NULL, const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3()) | |
| Same as the previous one, but with parameters in reverse order. | |
| Triangulation_3 (const Triangulation_3 &tr) | |
| Copy constructor. More... | |
| Triangulation_3 (InputIterator first, InputIterator last, const RegularTriangulationTraits_3 &traits=RegularTriangulationTraits_3(), Lock_data_structure *lock_ds=NULL) | |
Equivalent to constructing an empty triangulation with the optional traits class argument and calling insert(first,last). | |
| Triangulation_3 & | operator= (const Triangulation_3 &tr) |
The triangulation tr is duplicated, and modifying the copy after the duplication does not modify the original. More... | |
| void | swap (Triangulation_3 &tr) |
The triangulations tr and t are swapped. More... | |
| void | clear () |
Deletes all finite vertices and all cells of t. | |
| bool | operator== (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2) |
| Equality operator. More... | |
| bool | operator!= (const Triangulation_3< GT, Tds1 > &t1, const Triangulation_3< GT, Tds2 > &t2) |
The opposite of operator==. | |
|
const RegularTriangulationTraits_3 & | geom_traits () const |
| Returns a const reference to the geometric traits object. | |
|
const TriangulationDataStructure_3 & | tds () const |
| Returns a const reference to the triangulation data structure. | |
| TriangulationDataStructure_3 & | tds () |
| Returns a reference to the triangulation data structure. More... | |
| int | dimension () const |
| Returns the dimension of the affine hull. | |
| size_type | number_of_vertices () const |
| Returns the number of finite vertices. | |
| size_type | number_of_cells () const |
Returns the number of cells or 0 if t.dimension() < 3. | |
| Vertex_handle | infinite_vertex () |
| Returns the infinite vertex. | |
| void | set_infinite_vertex (Vertex_handle v) |
| This is an advanced function. More... | |
| Cell_handle | infinite_cell () const |
| Returns a cell incident to the infinite vertex. | |
| size_type | number_of_facets () const |
| The number of facets. More... | |
| size_type | number_of_edges () const |
| The number of edges. More... | |
| size_type | number_of_finite_cells () const |
| The number of finite cells. More... | |
| size_type | number_of_finite_facets () const |
| The number of finite facets. More... | |
| size_type | number_of_finite_edges () const |
| The number of finite edges. More... | |
| Tetrahedron | tetrahedron (Cell_handle c) const |
Returns the tetrahedron formed by the four vertices of c. More... | |
| Triangle | triangle (Cell_handle c, int i) const |
Returns the triangle formed by the three vertices of facet (c,i). More... | |
| Triangle | triangle (const Facet &f) const |
Same as the previous method for facet f. More... | |
| Segment | segment (const Edge &e) const |
Returns the line segment formed by the vertices of e. More... | |
| Segment | segment (Cell_handle c, int i, int j) const |
Same as the previous method for edge (c,i,j). More... | |
| const Point & | point (Cell_handle c, int i) const |
Returns the point given by vertex i of cell c. More... | |
| const Point & | point (Vertex_handle v) const |
Same as the previous method for vertex v. More... | |
| bool | is_infinite (Vertex_handle v) const |
true, iff vertex v is the infinite vertex. | |
| bool | is_infinite (Cell_handle c) const |
true, iff c is incident to the infinite vertex. More... | |
| bool | is_infinite (Cell_handle c, int i) const |
true, iff the facet i of cell c is incident to the infinite vertex. More... | |
| bool | is_infinite (const Facet &f) const |
true iff facet f is incident to the infinite vertex. More... | |
| bool | is_infinite (Cell_handle c, int i, int j) const |
true, iff the edge (i,j) of cell c is incident to the infinite vertex. More... | |
| bool | is_infinite (const Edge &e) const |
true iff edge e is incident to the infinite vertex. More... | |
| bool | is_vertex (const Point &p, Vertex_handle &v) const |
Tests whether p is a vertex of t by locating p in the triangulation. More... | |
| bool | is_vertex (Vertex_handle v) const |
Tests whether v is a vertex of t. | |
| bool | is_edge (Vertex_handle u, Vertex_handle v, Cell_handle &c, int &i, int &j) const |
Tests whether (u,v) is an edge of t. More... | |
| bool | is_facet (Vertex_handle u, Vertex_handle v, Vertex_handle w, Cell_handle &c, int &i, int &j, int &k) const |
Tests whether (u,v,w) is a facet of t. More... | |
| bool | is_cell (Cell_handle c) const |
Tests whether c is a cell of t. | |
| bool | is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c, int &i, int &j, int &k, int &l) const |
Tests whether (u,v,w,x) is a cell of t. More... | |
| bool | is_cell (Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle x, Cell_handle &c) const |
Tests whether (u,v,w,x) is a cell of t and computes this cell c. More... | |
| bool | has_vertex (const Facet &f, Vertex_handle v, int &j) const |
If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true. More... | |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v, int &j) const |
Same for facet (c,i). More... | |
| bool | has_vertex (const Facet &f, Vertex_handle v) const |
| bool | has_vertex (Cell_handle c, int i, Vertex_handle v) const |
| Same as the first two methods, but these two methods do not return the index of the vertex. | |
| bool | are_equal (Cell_handle c, int i, Cell_handle n, int j) const |
| bool | are_equal (const Facet &f, const Facet &g) const |
| bool | are_equal (const Facet &f, Cell_handle n, int j) const |
| For these three methods: More... | |
| Cell_handle | locate (const Point &query, Cell_handle start=Cell_handle(), bool *could_lock_zone=NULL) const |
If the point query lies inside the convex hull of the points, the cell that contains the query in its interior is returned. More... | |
| Cell_handle | locate (const Point &query, Vertex_handle hint, bool *could_lock_zone=NULL) const |
Same as above but uses hint as the starting place for the search. | |
| Cell_handle | locate (const Point &query, Locate_type <, int &li, int &lj, Cell_handle start=Cell_handle(), bool *could_lock_zone=NULL) const |
If query lies inside the affine hull of the points, the \( k\)-face (finite or infinite) that contains query in its interior is returned, by means of the cell returned together with lt, which is set to the locate type of the query (VERTEX, EDGE, FACET, CELL, or OUTSIDE_CONVEX_HULL if the cell is infinite and query lies strictly in it) and two indices li and lj that specify the \( k\)-face of the cell containing query. More... | |
| Cell_handle | locate (const Point &query, Locate_type <, int &li, int &lj, Vertex_handle hint, bool *could_lock_zone=NULL) const |
Same as above but uses hint as the starting place for the search. | |
| Cell_handle | inexact_locate (const Point &query, Cell_handle start=Cell_handle()) const |
Same as locate() but uses inexact predicates. More... | |
| Bounded_side | side_of_cell (const Point &p, Cell_handle c, Locate_type <, int &li, int &lj) const |
Returns a value indicating on which side of the oriented boundary of c the point p lies. More... | |
| Bounded_side | side_of_facet (const Point &p, const Facet &f, Locate_type <, int &li, int &lj) const |
Returns a value indicating on which side of the oriented boundary of f the point p lies: More... | |
| Bounded_side | side_of_facet (const Point &p, Cell_handle c, Locate_type <, int &li, int &lj) const |
Same as the previous method for the facet (c,3). | |
| Bounded_side | side_of_edge (const Point &p, const Edge &e, Locate_type <, int &li) const |
Returns a value indicating on which side of the oriented boundary of e the point p lies: More... | |
| Bounded_side | side_of_edge (const Point &p, Cell_handle c, Locate_type <, int &li) const |
| Same as the previous method for edge \( (c,0,1)\). | |
| bool | flip (Edge e) |
| bool | flip (Cell_handle c, int i, int j) |
Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive). More... | |
| bool | flip (Facet f) |
| bool | flip (Cell_handle c, int i) |
Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive). More... | |
| void | flip_flippable (Edge e) |
| void | flip_flippable (Cell_handle c, int i, int j) |
| Should be preferred to the previous methods when the edge is known to be flippable. More... | |
| void | flip_flippable (Facet f) |
| void | flip_flippable (Cell_handle c, int i) |
| Should be preferred to the previous methods when the facet is known to be flippable. More... | |
| Vertex_handle | insert (const Point &p, Cell_handle start=Cell_handle()) |
Inserts point p in the triangulation and returns the corresponding vertex. More... | |
| Vertex_handle | insert (const Point &p, Vertex_handle hint) |
Same as above but uses hint as the starting place for the search. | |
| Vertex_handle | insert (const Point &p, Locate_type lt, Cell_handle loc, int li, int lj) |
Inserts point p in the triangulation and returns the corresponding vertex. More... | |
| std::ptrdiff_t | insert (InputIterator first, InputIterator last) |
Inserts the points in the range [first,last). More... | |
| Vertex_handle | insert_in_cell (const Point &p, Cell_handle c) |
Inserts point p in cell c. More... | |
| Vertex_handle | insert_in_facet (const Point &p, const Facet &f) |
Inserts point p in facet f. More... | |
| Vertex_handle | insert_in_facet (const Point &p, Cell_handle c, int i) |
As above, insertion in facet (c,i). More... | |
| Vertex_handle | insert_in_edge (const Point &p, const Edge &e) |
Inserts p in edge e. More... | |
| Vertex_handle | insert_in_edge (Point p, Cell_handle c, int i, int j) |
As above, inserts p in edge \( (i, j)\) of c. More... | |
| Vertex_handle | insert_outside_convex_hull (const Point &p, Cell_handle c) |
The cell c must be an infinite cell containing p. More... | |
| Vertex_handle | insert_outside_affine_hull (const Point &p) |
p is linked to all the points, and the infinite vertex is linked to all the points (including p) to triangulate the new infinite face, so that all the points now belong to the boundary of the convex hull. More... | |
| Vertex_handle | insert_in_hole (Point p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i) |
| Creates a new vertex by starring a hole. More... | |
| Vertex_handle | insert_in_hole (Point p, CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i, Vertex_handle newv) |
Same as above, except that newv will be used as the new vertex, which must have been allocated previously with e.g. create_vertex. | |
| Finite_vertices_iterator | finite_vertices_begin () const |
| Starts at an arbitrary finite vertex. More... | |
| Finite_vertices_iterator | finite_vertices_end () const |
| Past-the-end iterator. | |
| Finite_edges_iterator | finite_edges_begin () const |
| Starts at an arbitrary finite edge. More... | |
| Finite_edges_iterator | finite_edges_end () const |
| Past-the-end iterator. | |
| Finite_facets_iterator | finite_facets_begin () const |
| Starts at an arbitrary finite facet. More... | |
| Finite_facets_iterator | finite_facets_end () const |
| Past-the-end iterator. | |
| Finite_cells_iterator | finite_cells_begin () const |
| Starts at an arbitrary finite cell. More... | |
| Finite_cells_iterator | finite_cells_end () const |
| Past-the-end iterator. | |
| All_vertices_iterator | all_vertices_begin () const |
| Starts at an arbitrary vertex. More... | |
| All_vertices_iterator | all_vertices_end () const |
| Past-the-end iterator. | |
| All_edges_iterator | all_edges_begin () const |
| Starts at an arbitrary edge. More... | |
| All_edges_iterator | all_edges_end () const |
| Past-the-end iterator. | |
| All_facets_iterator | all_facets_begin () const |
| Starts at an arbitrary facet. More... | |
| All_facets_iterator | all_facets_end () const |
| Past-the-end iterator. | |
| All_cells_iterator | all_cells_begin () const |
| Starts at an arbitrary cell. More... | |
| All_cells_iterator | all_cells_end () const |
| Past-the-end iterator. | |
| Point_iterator | points_begin () const |
| Iterates over the points of the triangulation. | |
| Point_iterator | points_end () const |
| Past-the-end iterator. | |
| Cell_circulator | incident_cells (Edge e) const |
Starts at an arbitrary cell incident to e. More... | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Cell_circulator | incident_cells (Edge e, Cell_handle start) const |
Starts at cell start. More... | |
| Cell_circulator | incident_cells (Cell_handle c, int i, int j, Cell_handle start) const |
As above for edge (i,j) of c. | |
| OutputIterator | incident_cells (Vertex_handle v, OutputIterator cells) const |
Copies the Cell_handles of all cells incident to v to the output iterator cells. More... | |
| OutputIterator | incident_facets (Vertex_handle v, OutputIterator facets) const |
Copies all Facets incident to v to the output iterator facets. More... | |
| bool | try_lock_and_get_incident_cells (Vertex_handle v, std::vector< Cell_handle > &cells) const |
Try to lock and copy the Cell_handles of all cells incident to v into cells. More... | |
| OutputIterator | finite_incident_cells (Vertex_handle v, OutputIterator cells) const |
Copies the Cell_handles of all finite cells incident to v to the output iterator cells. More... | |
| OutputIterator | finite_incident_facets (Vertex_handle v, OutputIterator facets) const |
Copies all finite Facets incident to v to the output iterator facets. More... | |
| OutputIterator | incident_edges (Vertex_handle v, OutputIterator edges) const |
Copies all Edges incident to v to the output iterator edges. More... | |
| OutputIterator | finite_incident_edges (Vertex_handle v, OutputIterator edges) const |
Copies all finite Edges incident to v to the output iterator edges. More... | |
| OutputIterator | adjacent_vertices (Vertex_handle v, OutputIterator vertices) const |
Copies the Vertex_handles of all vertices adjacent to v to the output iterator vertices. More... | |
| OutputIterator | finite_adjacent_vertices (Vertex_handle v, OutputIterator vertices) const |
Copies the Vertex_handles of all finite vertices adjacent to v to the output iterator vertices. More... | |
| size_type | degree (Vertex_handle v) const |
| Returns the degree of a vertex, that is, the number of incident vertices. More... | |
| Facet_circulator | incident_facets (Edge e) const |
Starts at an arbitrary facet incident to e. More... | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Edge e, Facet start) const |
Starts at facet start. More... | |
| Facet_circulator | incident_facets (Edge e, Cell_handle start, int f) const |
Starts at facet of index f in start. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Facet start) const |
As above for edge (i,j) of c. | |
| Facet_circulator | incident_facets (Cell_handle c, int i, int j, Cell_handle start, int f) const |
As above for edge (i,j) of c and facet (start,f). | |
| int | mirror_index (Cell_handle c, int i) const |
Returns the index of c in its \( i^{th}\) neighbor. More... | |
| Vertex_handle | mirror_vertex (Cell_handle c, int i) const |
Returns the vertex of the \( i^{th}\) neighbor of c that is opposite to c. More... | |
| Facet | mirror_facet (Facet f) const |
| Returns the same facet seen from the other adjacent cell. | |
| bool | is_valid (bool verbose=false) const |
| This is a function for debugging purpose. More... | |
| bool | is_valid (Cell_handle c, bool verbose=false) const |
| This is a function for debugging purpose. More... | |
| istream & | operator>> (istream &is, Triangulation_3 &t) |
Reads the underlying combinatorial triangulation from is by calling the corresponding input operator of the triangulation data structure class (note that the infinite vertex is numbered 0), and the non-combinatorial information by calling the corresponding input operators of the vertex and the cell classes (such as point coordinates), which are provided by overloading the stream operators of the vertex and cell types. More... | |
| ostream & | operator<< (ostream &os, const Triangulation_3 &t) |
Writes the triangulation t into os. | |
| void | set_lock_data_structure (Lock_data_structure *lock_ds) const |
| Set the pointer to the lock data structure. | |
| CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::Regular_triangulation_3 | ( | const RegularTriangulationTraits_3 & | traits = RegularTriangulationTraits_3(), |
| Lock_data_structure * | lock_ds = NULL |
||
| ) |
Creates an empty regular triangulation, possibly specifying a traits class traits.
lock_ds is an optional pointer to the lock data structure for parallel operations. It must be provided if concurrency is enabled.
Copy constructor.
The pointer to the lock data structure is not copied. Thus, the copy won't be concurrency-safe as long as the user has not called Triangulation_3::set_lock_data_structure.
| CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::Regular_triangulation_3 | ( | InputIterator | first, |
| InputIterator | last, | ||
| const RegularTriangulationTraits_3 & | traits = RegularTriangulationTraits_3(), |
||
| Lock_data_structure * | lock_ds = NULL |
||
| ) |
Equivalent to constructing an empty triangulation with the optional traits class argument and calling insert(first,last).
If parallelism is enabled, the points will be inserted in parallel.
| InputIterator | must be an input iterator with value type Weighted_point. |
| Bare_point CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::dual | ( | Cell_handle | c) | const |
Returns the weighted circumcenter of the four vertices of c.
rt.dimension() \( =3\) and c is not infinite. | Object CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::dual | ( | Facet | f) | const |
Returns the dual of facet f, which is.
in dimension 3: either a segment, if the two cells incident to f are finite, or a ray, if one of them is infinite;
in dimension 2: a point.
rt.dimension() \( \geq2\) and f is not infinite. | Triple<OutputIteratorBoundaryFacets, OutputIteratorCells, OutputIteratorInternalFacets> CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::find_conflicts | ( | const Weighted_point | p, |
| Cell_handle | c, | ||
| OutputIteratorBoundaryFacets | bfit, | ||
| OutputIteratorCells | cit, | ||
| OutputIteratorInternalFacets | ifit, | ||
| bool * | could_lock_zone = NULL, |
||
| const Facet * | this_facet_must_be_in_the_cz = NULL, |
||
| bool * | the_facet_is_in_its_cz = NULL |
||
| ) |
Compute the conflicts with p.
| p | The query point. |
| c | The starting cell. |
| cit | The cells (resp. facets) in conflict with p. |
| bfit | The facets (resp. edges) on the boundary of the conflict zone, that is, the facets (resp. edges) (t, i) where the cell (resp.. facet) t is in conflict, but t->neighbor(i) is not. |
| ifit | The facets (resp. edges) inside the conflict zone, that facets incident to two cells (resp. facets) in conflict. |
| could_lock_zone | The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. If the pointer is not null, the algorithm will try to lock all the cells of the conflict zone, i.e. all the vertices that are inside or on the boundary of the conflict zone (as a result, the boundary cells become partially locked). If it succeeds, *could_lock_zone is true, otherwise it is false (and the returned conflict zone is only partial). In any case, the locked cells are not unlocked by the function, leaving this choice to the user. |
| this_facet_must_be_in_the_cz | If the optional argument this_facet_must_be_in_the_cz is not null, the algorithm will check if this facet is in the conflict zone (it may be internal as well as boundary). |
| the_facet_is_in_its_cz | This argument must be not null if the previous this_facet_must_be_in_the_cz argument is not null. The boolean value pointed by this pointer is set to true if *this_facet_must_be_in_the_cz is among the internal or boundary facets of the conflict zone, and false otherwise. |
c must be in conflict with p. rt.dimension() \( \geq2\), and c is in conflict with p.Triple composed of the resulting output iterators. | Vertex_handle CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::insert | ( | const Weighted_point & | p, |
| Cell_handle | start = Cell_handle(), |
||
| bool * | could_lock_zone = NULL |
||
| ) |
Inserts weighted point p in the triangulation.
The optional argument start is used as a starting place for the search.
If this insertion creates a vertex, this vertex is returned.
If p coincides with an existing vertex and has a greater weight, then the existing weighted point becomes hidden (see RegularTriangulationCellBase_3) and p replaces it as vertex of the triangulation.
If p coincides with an already existing vertex (both point and weights being equal), then this vertex is returned and the triangulation remains unchanged.
Otherwise if p does not appear as a vertex of the triangulation, then it is stored as a hidden point and this method returns the default constructed handle.
The optional argument could_lock_zone is used by the concurrency-safe version of the triangulation. If the pointer is not null, the insertion will try to lock all the cells of the conflict zone, i.e. all the vertices that are inside or on the boundary of the conflict zone. If it succeeds, *could_lock_zone is true, otherwise it is false (and the point is not inserted). In any case, the locked cells are not unlocked by the function, leaving this choice to the user.
| Vertex_handle CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::insert | ( | const Weighted_point & | p, |
| Locate_type | lt, | ||
| Cell_handle | loc, | ||
| int | li, | ||
| int | lj, | ||
| bool * | could_lock_zone = NULL |
||
| ) |
Inserts weighted point p in the triangulation and returns the corresponding vertex.
Similar to the above insert() function, but takes as additional parameter the return values of a previous location query. See description of Triangulation_3::locate().
| std::ptrdiff_t CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::insert | ( | InputIterator | first, |
| InputIterator | last | ||
| ) |
Inserts the weighted points in the range [first,last).
It returns the difference of the number of vertices between after and before the insertions (it may be negative due to hidden points). Note that this function is not guaranteed to insert the points following the order of InputIterator, as spatial_sort() is used to improve efficiency. If parallelism is enabled, the points will be inserted in parallel.
| InputIterator | must be an input iterator with value type Weighted_point. |
| std::ptrdiff_t CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::insert | ( | WeightedPointWithInfoInputIterator | first, |
| WeightedPointWithInfoInputIterator | last | ||
| ) |
Inserts the weighted points in the iterator range [first,last).
It returns the difference of the number of vertices between after and before the insertions (it may be negative due to hidden points). Note that this function is not guaranteed to insert the weighted points following the order of WeightedPointWithInfoInputIterator, as spatial_sort() is used to improve efficiency. If parallelism is enabled, the points will be inserted in parallel. Given a pair (p,i), the vertex v storing p also stores i, that is v.point() == p and v.info() == i. If several pairs have the same point, only one vertex is created, one of the objects of type Vertex::Info will be stored in the vertex.
Vertex must be model of the concept TriangulationVertexBaseWithInfo_3. | (WeightedPointWithInfoInputIterator | must be an input iterator with value type std::pair<Weighted_point,Vertex::Info>. |
| Vertex_handle CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::insert_in_hole | ( | Weighted_point | p, |
| CellIt | cell_begin, | ||
| CellIt | cell_end, | ||
| Cell_handle | begin, | ||
| int | i | ||
| ) |
Creates a new vertex by starring a hole.
It takes an iterator range [cell_begin,cell_end) of Cell_handles which specifies a hole: a set of connected cells (resp. facets in dimension 2) which is star-shaped wrt p. (begin, i) is a facet (resp. an edge) on the boundary of the hole, that is, begin belongs to the set of cells (resp. facets) previously described, and begin->neighbor(i) does not. Then this function deletes all the cells (resp. facets) describing the hole, creates a new vertex v, and for each facet (resp. edge) on the boundary of the hole, creates a new cell (resp. facet) with v as vertex. Then v->set_point(p) is called and v is returned.
If the hole contains interior vertices, each of them is hidden by the insertion of p and is stored in the new cell which contains it.
rt.dimension() \( \geq2\), the set of cells (resp. facets in dimension 2) is connected, not empty, its boundary is connected, and p lies inside the hole, which is star-shaped wrt p. | bool CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::is_valid | ( | bool | verbose = false) | const |
This is a function for debugging purpose.
Checks the combinatorial validity of the triangulation and the validity of its geometric embedding (see Section Representation). Also checks that all the power spheres (resp. power circles in dimension 2, power segments in dimension 1) of cells (resp. facets in dimension 2, edges in dimension 1) are regular. When verbose is set to true, messages describing the first invalidity encountered are printed. This method is mainly a debugging help for the users of advanced features.
| Vertex_handle CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::nearest_power_vertex | ( | Weighted_point | p, |
| Cell_handle | c = Cell_handle() |
||
| ) |
Returns the vertex of the triangulation which is nearest to \( p\) with respect to the power distance.
This means that the power of the query point p with respect to the weighted point in the returned vertex is smaller than the power of p with respect to the weighted point in any other vertex. Ties are broken arbitrarily. The default constructed handle is returned if the triangulation is empty. The optional argument c is a hint specifying where to start the search.
c is a cell of rt. | bool CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::remove | ( | Vertex_handle | v, |
| bool * | could_lock_zone | ||
| ) |
Removes the vertex v from the triangulation.
This function is concurrency-safe if the triangulation is concurrency-safe. It will first try to lock all the cells adjacent to v. If it succeeds, *could_lock_zone is true, otherwise it is false (and the point is not removed). In any case, the locked cells are not unlocked by the function, leaving this choice to the user.
This function will try to remove v only if the removal does not decrease the dimension. The return value is only meaningful if *could_lock_zone is true:
v is a finite vertex of the triangulation. dt.dimension() \( =3\). | int CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::remove | ( | InputIterator | first, |
| InputIterator | beyond | ||
| ) |
Removes the vertices specified by the iterator range [first, beyond).
The number of vertices removed is returned. If parallelism is enabled, the points will be removed in parallel. Note that if at some step, the triangulation dimension becomes lower than 3, the removal of the remaining points will go on sequentially.
| InputIterator | must be an input iterator with value type Vertex_handle. |
| Bounded_side CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::side_of_power_circle | ( | const Facet & | f, |
| const Weighted_point & | p | ||
| ) | const |
Returns the position of the point p with respect to the power circle of f.
More precisely, it returns:
ON_BOUNDARY if p is orthogonal to the power circle in the plane of the facet,
ON_UNBOUNDED_SIDE when their angle is less than \( \pi/2\),
ON_BOUNDED_SIDE when it is greater than \( \pi/2\) (see Figure Triangulation3figsidedim2).
f.first, and does the same as in dimension 2 in this plane.ON_BOUNDARY if p is orthogonal to the circle,
ON_UNBOUNDED_SIDE when the angle between p and the power circle of f is less than \( \pi/2\), ON_BOUNDED_SIDE when it is greater than \( \pi/2\).
ON_BOUNDED_SIDE for a point in the open half plane defined by f and not containing any other point of the triangulation,
ON_UNBOUNDED_SIDE in the other open half plane.
If the point p is collinear with the finite edge e of f, it returns:
ON_BOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(e)}^{(w)})<0\), where \( {z(e)}^{(w)}\) is the power segment of e in the line supporting e,
ON_BOUNDARY if \( \Pi({p}^{(w)}-{z(e)}^{(w)})=0\),
ON_UNBOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(e)}^{(w)})>0\) .
rt.dimension() \( \geq2\). | Bounded_side CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::side_of_power_segment | ( | Cell_handle | c, |
| const Weighted_point & | p | ||
| ) | const |
In dimension 1, returns.
ON_BOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(c)}^{(w)})<0\), where \( {z(c)}^{(w)}\) is the power segment of the edge represented by c,
ON_BOUNDARY if \( \Pi({p}^{(w)}-{z(c)}^{(w)})=0\),
ON_UNBOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(c)}^{(w)})>0\) .
rt.dimension() \( = 1\). | Bounded_side CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::side_of_power_sphere | ( | Cell_handle | c, |
| const Weighted_point & | p | ||
| ) | const |
Returns the position of the weighted point \( p\) with respect to the power sphere of c.
More precisely, it returns:
ON_BOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(c)}^{(w)})<0\) where \( {z(c)}^{(w)}\) is the power sphere of c. For an infinite cell this means either that p lies strictly in the half space limited by its finite facet and not containing any other point of the triangulation, or that the angle between p and the power circle of the finite facet of c is greater than \( \pi/2\).ON_BOUNDARY if p is orthogonal to the power sphere of c i.e. \( \Pi({p}^{(w)}-{z(c)}^{(w)})=0\). For an infinite cell this means that p is orthogonal to the power circle of its finite facet.ON_UNBOUNDED_SIDE if \( \Pi({p}^{(w)}-{z(c)}^{(w)})>0\) i.e. the angle between the weighted point p and the power sphere of c is less than \( \pi/2\) or if these two spheres do not intersect. For an infinite cell this means that p does not satisfy either of the two previous conditions. rt.dimension() \( =3\). | OutputIterator CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::vertices_in_conflict | ( | Weighted_point | p, |
| Cell_handle | c, | ||
| OutputIterator | res | ||
| ) |
vertices_on_conflict_zone_boundary since CGAL-3.8. | OutputIterator CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::vertices_inside_conflict_zone | ( | Weighted_point | p, |
| Cell_handle | c, | ||
| OutputIterator | res | ||
| ) |
Similar to find_conflicts(), but reports the vertices which are in the interior of the conflict zone of p, in the output iterator res.
The vertices that are on the boundary of the conflict zone are not reported. Returns the resulting output iterator.
rt.dimension() \( \geq2\), and c is a cell containing p. | OutputIterator CGAL::Regular_triangulation_3< RegularTriangulationTraits_3, TriangulationDataStructure_3, SurjectiveLockDataStructure >::vertices_on_conflict_zone_boundary | ( | Weighted_point | p, |
| Cell_handle | c, | ||
| OutputIterator | res | ||
| ) |
Similar to find_conflicts(), but reports the vertices which are on the boundary of the conflict zone of p, in the output iterator res.
Returns the resulting output iterator.
rt.dimension() \( \geq2\), and c is a cell containing p.