|
CGAL 4.8.1 - Polynomial
|
|
CGAL 4.8.1 - Polynomial
|
Note: This functor is optional!
Computes the Sturm-Habicht sequence (aka the signed subresultant sequence) of a polynomial \( f\) of type PolynomialTraits_d::Polynomial_d with respect to a certain variable \( x_i\). The Sturm-Habicht sequence is similar to the polynomial subresultant sequence of \( f\) and its derivative \( f':=\frac{\partial f}{\partial x_i}\) with respect to \( x_i\). The implementation is based on the following definition:
Let \( n:=\deg f\) and \( \delta_k:=(-1)^{k(k+1)/2}\). For \( k\in\{0,\ldots,n\}\), the \( k\)-th Sturm-Habicht polynomial of \( f\) is defined as:
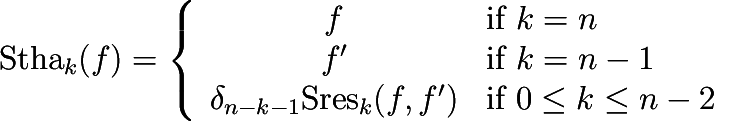
where \( \mathrm{Sres}_k(f,f')\) is defined as in the concept PolynomialTraits_d::PolynomialSubresultants.
The result is written in an output range, starting with the \( 0\)-th Sturm-Habicht polynomial (which is equal to the discriminant of \( f\) up to a multiple of the leading coefficient).
Operations | |
| template<typename OutputIterator > | |
| OutputIterator | operator() (Polynomial_d f, OutputIterator out) |
| computes the Sturm-Habicht sequence of \( f\), with respect to the outermost variable. More... | |
| template<typename OutputIterator > | |
| OutputIterator | operator() (Polynomial_d f, OutputIterator out, int i) |
| computes the Sturm-Habicht sequence of \( f\) with respect to the variable \( x_i\). | |
| OutputIterator PolynomialTraits_d::SturmHabichtSequence::operator() | ( | Polynomial_d | f, |
| OutputIterator | out | ||
| ) |
computes the Sturm-Habicht sequence of \( f\), with respect to the outermost variable.
Each element is of type PolynomialTraits_d::Polynomial_d.