|
CGAL 4.8.2 - Combinatorial Maps
|
|
CGAL 4.8.2 - Combinatorial Maps
|
A d-dimensional combinatorial map is a data structure representing an orientable subdivided d-dimensional object obtained by taking dD cells, and allowing to glue dD cells along (d-1)D cells. It provides a description of all the cells of the subdivision (for example vertices and edges), together with incidence and adjacency relationships. This package is a generalization of the halfedge data structure to higher dimension. Indeed, a 2D combinatorial map is equivalent to a halfedge data structure: there is a one-to-one mapping between elements of both data structures, halfedges corresponding to darts.
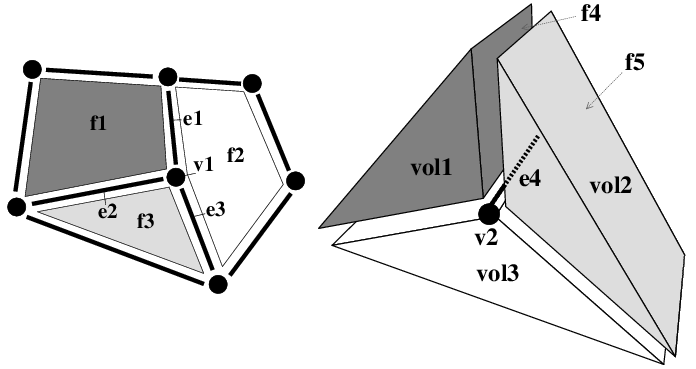
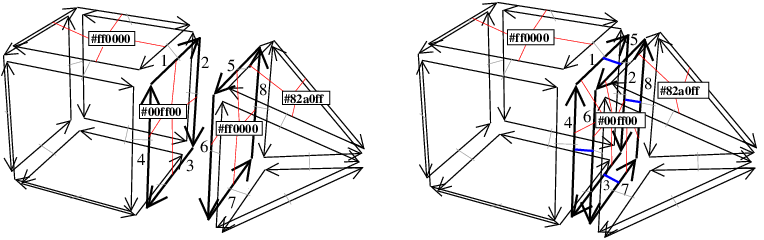
We denote i-cell for an i-dimensional cell (for example in 3D, 0-cells are vertices, 1-cells are edges, 2-cells are facets, and 3-cells are volumes). A boundary relation is defined on these cells, giving for each i-cell c the set of (i-1)-cells contained in the boundary of c. Two cells c1 and c2 are incident if there is a path of cells, starting from the cell of biggest dimension to the other cell, such that each cell of the path (except the first one) belongs to the boundary of the previous cell in the path. Two i-cells c3 and c4 are adjacent if there is an (i-1)-cell incident to both c3 and c4. You can see an example of a 2D object and a 3D object in Figure 27.1 showing some cells of the subdivision and some adjacency and incidence relations.
A combinatorial map is an edge-centered data structure describing the cells and the incidence and adjacency relations, using only one basic element called dart, and a set of pointers between these darts. A dart can be thought as a part of an oriented edge (1-cell), together with a part of incident cells of dimensions 0, 2, 3, ..., d. When a dart d0 describes a part of an i-cell c, we say that d0 belongs to c, and that c contains d0. Let us look at the example in Figure 27.2 showing the 2D and 3D combinatorial maps describing the two objects given in Figure 27.1.
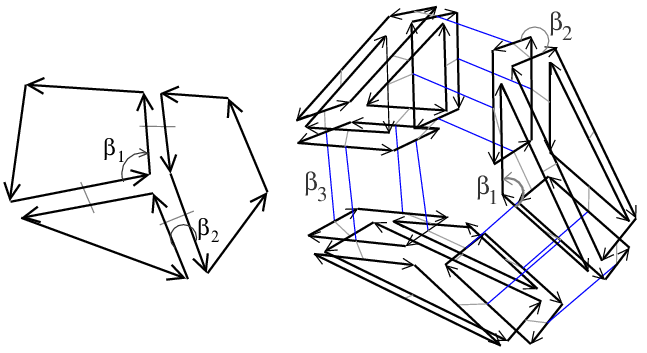
First let us start in 2D (Figure 27.2 (Left)). Facet f1 is described by four darts. These darts are linked together with pointers. Starting from a dart and following a \( \beta_1\) pointer, we get to a dart which belongs to the same facet but to the next edge (1-cell, which explains the index 1 of \( \beta_1\)). Starting from any dart and following \( \beta_1\) pointers, we can reach exactly all the darts describing the facet. Starting from a dart and following a \( \beta_2\) pointer, we get to a dart which belongs to the same edge but to the neighboring facet (2-cell, which explains the index 2 of \( \beta_2\)). Starting from any dart and following \( \beta_2\) pointers, we can reach exactly all the darts describing the edge (in 2D one or two darts).
Things are slightly different for vertices. Indeed, each \( \beta_i\) points to a dart belonging to a different i-cell, but also to a different 0-cell (vertex). This is so because two linked darts have opposite orientations. For this reason, starting from any dart belonging to a vertex v, we have to follow \( \beta_2\) then \( \beta_1\) to reach exactly the darts describing the vertex v. In fact, by composing two \( \beta_i\)s, we always obtain a dart belonging to the same vertex (if we do not start by following a \( \beta_1\) pointer).
The main interest of combinatorial map definition based on darts and \( \beta_i\) pointers is to be able to increase the dimension "only" by adding new pointers. We can verify this fact by studying the 3D example (Figure 27.2 (Right)). In addition to \( \beta_1\) and \( \beta_2\) of the 2D case, there is a new pointer \( \beta_3\).
If we take a closer look at the central edge e4 shown in Figure 27.3 (Left), we can see that it is described by six darts linked together. Starting from a dart and following a \( \beta_3\) pointer, we get to a dart which belongs to the same edge, to the same facet, but to the neighboring volume (a 3-cell, which explains the index 3 in \( \beta_3\)). Similarly, starting from a dart and following a \( \beta_2\) pointer, we get to a dart which belongs to the same edge, to the same volume, but to the neighboring facet (2-cell). Starting from any of these six darts and following \( \beta_2\) and \( \beta_3\) pointers, we can reach exactly the six darts describing edge e4.
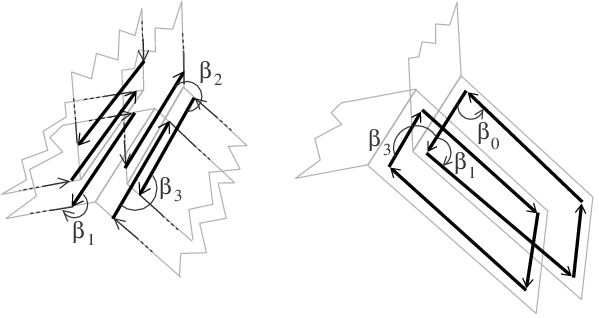
For facets, by following a \( \beta_1\) pointer, we get to a dart which belongs to the same facet, to the same volume, but to the next edge (1-cell, which explains the index 1 of \( \beta_1\)). Starting from any dart and following \( \beta_1\) and \( \beta_3\) pointers, we can reach exactly all the darts describing the facet (see Figure 27.3 (Right)). For volumes, starting from any dart and following \( \beta_1\) and \( \beta_2\) pointers, we can reach exactly all the darts describing the volume.
For vertices, we have to follow \( \beta_2\) then \( \beta_1\), and \( \beta_3\) then \( \beta_1\) to reach exactly the darts describing the vertex v. Indeed, as in 2D, we have to compose two \( \beta_i\)s to obtain a dart belonging to the same vertex (if we do not start by following a \( \beta_1\) pointer).
In some cases, the general rule that by following a \( \beta_i\) we get a dart which belongs to the neighboring i-cell is not true, as for example for darts belonging to the boundary of the represented object. For example, in Figure 27.1 (Left), any dart d0 that does not belong to edge e1, e2 and e3 belongs to a 2-cell, and there is no neighboring facet along the edge containing d0. Another example is in Figure 27.1 (Right), for any dart d0 that belongs to facet f5. d0 belongs to volume vol2, but there is no neighboring volume along this facet. The general rule is also not true for unbounded cells. For example if we remove a dart in Figure 27.2 (Left), we obtain an unbounded facet having a dart without next dart for \( \beta_1\), and if we remove a facet in Figure 27.2 (Right), we obtain an unbounded volume having some darts without neighboring facet for \( \beta_2\). In such a case, there is a particular value called \( \varnothing\) used to describe that a dart d0 is not linked to another dart in dimension i.
Combinatorial maps are defined in any dimension. A 0D combinatorial map is a set of isolated darts describing isolated vertices. A 1D combinatorial map describes paths or cycles of darts corresponding to paths or cycles of edges, and equivalent to double linked lists. The most useful cases are 2D and 3D combinatorial maps. Since 2D combinatorial maps are equivalent to halfedge data structure, notions are illustrated in 3D in the following examples to help the reader understand this specific case. But it is important to keep in mind that one main interest of combinatorial maps is their generic definition in any dimension, and that everything presented in this manual is valid in any dimension.
A dD combinatorial map is useful when you want to describe dD objects and the adjacency relations between these objects, and you want to be able to efficiency traverse these objects by using the different relations. For example, we can use a 3D combinatorial map to describe a 3D segmented image: each 3-cell corresponds to a region in the image and each 2-cell corresponds to a contact area between two regions.
A combinatorial map does not contain any geometrical information. However, this package allows to associate any information to the cells of the combinatorial map. A specific information, which is often used in practice, consists in adding linear geometry to a combinatorial map by associating a point to each vertex of the map: this is the object of the Linear cell complex package (when an object has a point associated to each vertex, each edge is thus a straight line segment, which explains the name "linear geometry"). The Linear cell complex package can for example be useful to describe 3D buildings as set of walls, rooms, doors and windows (both combinatorial and geometrical descriptions) and all the adjacency relations between these elements allowing for example to move a camera in a given building from rooms to rooms by traversing doors.
In this section, we describe dD combinatorial maps in terms of data structure and operations. Mathematical definitions are provided in Section Mathematical Definitions, and a package description is given in Section Software Design.
A dD combinatorial map is a set of darts D. A dart d0 is an element that can be linked with d+1 darts by pointers called \( \beta_i\), with 0 \( \leq\)i \( \leq\)d. Dart d0 is said i-free when \( \beta_i\)(d0)= \( \varnothing\). Each \( \beta_i\), for 2 \( \leq\)i \( \leq\)d, is its own inverse, i.e., if dart d0 is not i-free, then \( \beta_i\)( \( \beta_i\)(d0))=d0. This is different for \( \beta_0\) and \( \beta_1\): \( \beta_0\) is the inverse of \( \beta_1\), i.e., if darts d1 and d2 are such that \( \beta_1\)(d1)=d2, then \( \beta_0\)(d2)=d1. Given dart d1, if there is no dart d2 such that \( \beta_1\)(d2)=d1, then \( \beta_0\)(d1)= \( \varnothing\). \( \varnothing\) is a constant, which does not belong to the set of darts D of the combinatorial map. However, by definition \( \varnothing\) is linked with itself for all \( \beta_i\)s: \( \forall\)i, 0 \( \leq\)i \( \leq\)d, \( \beta_i\)( \( \varnothing)\)= \( \varnothing\).
A combinatorial map is without i-boundary if there is no i-free dart, and it is without boundary if it is without i-boundary for all dimensions 1 \( \leq\)i \( \leq\)d.
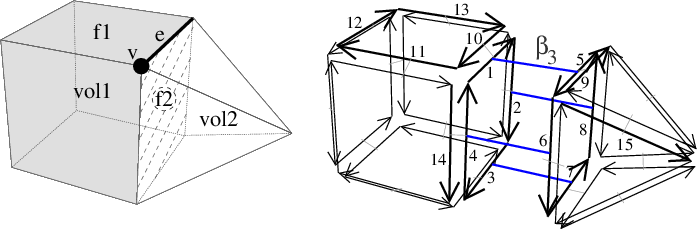
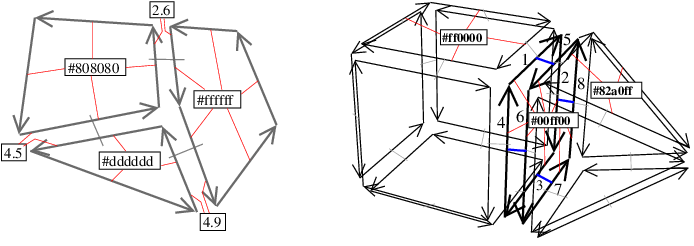
We show in Figure 27.4 a 3D object and the corresponding 3D combinatorial map. This map has 40 darts represented by arrows, some darts being numbered. In this combinatorial map, we have for example \( \beta_1\)(1)=2, \( \beta_2\)(1)=10, and \( \beta_3\)(1)=5. This combinatorial map is without 1-boundary and 2-boundary, but has some 3-boundary, because some darts are 3-free, for example \( \beta_3\)(10)= \( \varnothing\) and \( \beta_3\)(12)= \( \varnothing\).
A cell in a dD combinatorial map is implicitly represented by a subset of darts. In this section, we will see how to retrieve all cells containing a given dart, how to retrieve all darts belonging to a cell containing a given dart, and how incidence and adjacency relations are defined in terms of darts.
The first important property of a combinatorial map is that each dart belongs to an i-cell, \( \forall\)i, 0 \( \leq\)i \( \leq\)d. For example in 3D, a dart belongs to a vertex, an edge, a facet, and a volume. This means that a 3D combinatorial map containing an isolated dart contains exactly one vertex, one edge, one facet and one volume.
The second important property is that cells of a combinatorial map correspond to specific orbits. Given a set S \( \subseteq\){ \( \beta_1\),..., \( \beta_d\)} and a dart d0, the orbit \( \langle{}\) S \( \rangle{}\)(d0) is the set of darts that can be reached from d0 by following any combination of any \( \beta_i\)'s in S and their inverses (to simplify notations, we can use for example \( \langle{}\) \( \beta_1\), \( \beta_4\) \(\rangle{}\)(d0) to denote \( \langle{}\) S \( \rangle{}\)(d0) with S={ \( \beta_1\), \( \beta_4\)}).
Given a dart d0, in general, \( \beta_i\)(d0) (with 1 \( \leq\)i \( \leq\)d) belongs to the same cells as d0, only the i-cell and 0-cell are different. There are two exceptions:
Since \( \beta_i\)(d0) (with 1 \( \leq\)i \( \leq\)d) allows to change the current i-cell, all the darts that can be reached from d0 by using any combination of \( \beta_j\)'s, \( \forall\)j, 1 \( \leq\)j \( \leq\)d and j \( \neq\)i and their inverse are contained in the same i-cell as d0. The i-cell containing d0 is defined in terms of orbit by \( \langle{}\) \( \beta_1\),..., \( \beta_{i-1}\), \( \beta_{i+1}\),..., \( \beta_d\) \( \rangle{}\)(d0).
There is a special case for vertices. Given a dart d0, the set of darts contained in the same vertex as d0 are the darts that can be reached from d0 by using any combination of \(\beta_i \circ\) \( \beta_j\), \( \forall\)i,j, 1 \( \leq\)i \( <\)j \( \leq\)d, and their inverse. The 0-cell containing d0 is defined in terms of orbit by \( \langle{}\){ \( \beta_i\) \( \circ\) \( \beta_j\) \( |\) \( \forall\)i,j: 1 \( \leq\)i \( <\)j \( \leq\)d} \( \rangle{}\)(d0).
Orbit \( \langle{}\) \( \beta_1\),..., \( \beta_d\) \( \rangle{}\)(d0) is the connected component containing dart d0. A combinatorial map is connected if this set is equal to the set of all the darts of the combinatorial map.
A last important property of cells is that for all dimensions i the set of i-cells forms a partition of the set of darts D, i.e. for any i, the union of the sets of darts of all the i-cells is equal to D, and the sets of darts of two different i-cells are disjoint.
Let us give some examples of cells in 3D, for the 3D combinatorial map of Figure 27.4 :
Using this definition of cells as sets of darts, we can retrieve all the incidence and adjacency relations between the cells of the subdivision in a combinatorial map. Two cells are incident if the intersection of their two sets of darts is non empty (whatever the dimension of the two cells). Two i-cells c1 and c2, 1 \( \leq\)i \( \leq\)d, are adjacent if there is d1 \( \in\)c1 and d2 \( \in\)c2 such that d1= \( \beta_i\)(d2) (or d2= \( \beta_i\)(d1) for i=1).
In the example of Figure 27.4, vertex v and edge e are incident since the intersection of the two corresponding sets of darts is {1,9} \( \neq\) \( \emptyset\). Vertex v is incident to facet f2 since the intersection of the two corresponding sets of darts is {1,6} \( \neq\) \( \emptyset\). Edge e and facet f1 are incident since the intersection of the two corresponding sets of darts is {10} \( \neq\) \( \emptyset\). Finally, facets f1 and f2 are adjacent because 10 \( \in\)f1, 1 \( \in\)f2 and 10= \( \beta_2\)(1).
We can consider i-cells in a dimension d' with i \( \leq\)d' \( \leq\) d. The idea is to consider the i-cells as if the combinatorial map was in d' dimension. For that, we only take into account the \( \beta_j \)s for j \( \leq\)d'. The i-cell containing d0 in dimension d' is the orbit \( \langle{}\) \( \beta_1\),..., \( \beta_{i-1}\), \( \beta_{i+1}\),..., \( \beta_{d'}\) \( \rangle{}\)(d0), and the 0-cell is the orbit \( \langle{}\){ \( \beta_i\) \( \circ\) \( \beta_j\) \( |\) \( \forall\)i,j: 2 \( \leq\)i \( <\)j \( \leq\)d'} \( \rangle{}\)(d0). By default, i-cells are considered in dimension d, the dimension of the combinatorial map.
In the example of Figure 27.4, the 2-cell containing dart 1 is facet f2 which is the set of darts {1,2,3,4,5,6,7,8}. If we consider the same 2-cell in dimension 2, we obtain the set of darts {1,2,3,4}. Intuitively we "forget" \( \beta_3\) and we obtain the set of darts of the facet containing dart 1 restricted to the volume containing this dart.
Combinatorial maps only describe the cells of the subdvision, and all the incidence and adjacency relations between these cells. This is not enough for many applications which need to associate information to cells. This can be geometric or non-geometric information, such as 3D points associated to vertices, the edge length associated to edges, or a color or normal to a facet.
To answer this need, a combinatorial map allows to create attributes which are able to store any information, and to associate attributes to cells of the combinatorial map. We denote i-attributes for the attributes associated with i-cells. Attributes may exist for only some of the dimensions, and if they exist for dimension i, they do not necessarily exist for each of the i-cells. More precisely, i-attributes are associated to i-cells by an injection:
Since i-cells are not explicitely represented in combinatorial maps, the association between i-cells and i-attributes is transferred to darts: if attribute a is associated to i-cell c, all the darts belonging to c are associated to a.
We can see two examples of combinatorial maps having some attributes in Figure 27.5. In the first example (Left), a 2D combinatorial map has 1-attributes containing a float, for example corresponding to the length of the associated 1-cell, and 2-attributes containing a color in RGB format. In the second example (Right), a 3D combinatorial map has 2-attributes containing a color in RGB format.
There are some conditions that a combinatorial map must satisfy to be valid. Some of them have already been given about the \( \beta\) pointers (see Section Combinatorial Map and Darts) and about the association between darts and attributes (see Section How to Associate Information to Cells).
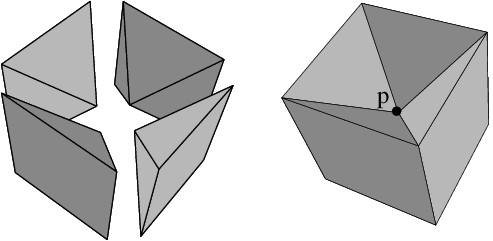
There is an additional condition related to the type of represented objects, which are quasi-manifold orientable dD objects. A dD quasi-manifold is an object obtained by taking some isolated d-cells, and allowing to glue d-cells along (d-1)-cells. It is orientable if it is possible to embed it in the Euclidean space and to define a global "left" and "right" direction in each point of the embedded object. In 2D, quasi-manifolds are manifolds, but this is no longer true in higher dimension as we can see in the example presented in Figure 27.6. In this example, the object to the right is not a manifold since the neighborhood of the point p in the object is not homeomorphic to a 3D ball (intuitively, two objects are homeomorphic if each object can be continuously deformed into the second one; in such a case, the two objects have exactly the same topological properties).
Combinatorial maps can only represent quasi-manifolds due to the definition of \( \beta\) pointers. As we have seen in Section Cells as Sets of Darts, \( \beta_i\)(d0) (with 1 \( \leq\)i \( \leq\)d) belongs to the same cells as d0, only the i-cell and 0-cell are different. In other words, \( \beta_i\) links two i-cells that share a common (i-1)-cell: it is not possible to link more than two i-cells along a same (i-1)-cell. For this reason, it is not possible to describe non quasi-manifold objects as those shown in Figure 27.7 by combinatorial maps.
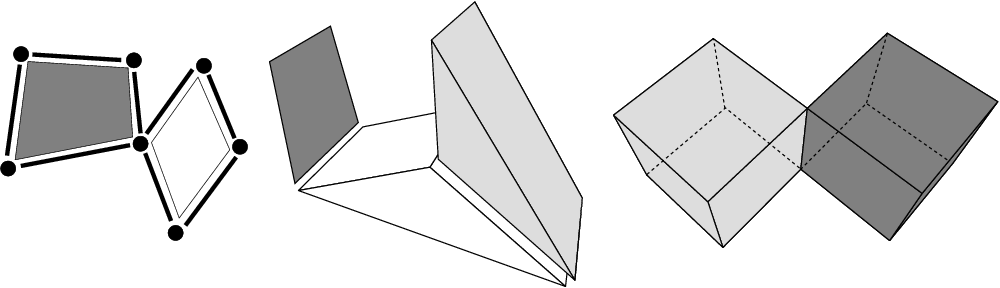
Due to this additional condition, any objects can not be represented by a combinatorial map but only orientable quasi-manifolds. We need to study now the inverse relation. Does any set of darts linked together by \( \beta_i\)'s, with 0 \( \leq\)i \( \leq\)d correspond to a quasi-manifold? As we can see in Figure 27.8, the answer is no.
In the first example (Left), there are two 3-cells (one to the left for the cube, a second to the right for the pyramid) which are "partially adjacent" along one 2-cell. Indeed, only two darts of the 2-cell are linked by \( \beta_3\). We have \( \beta_3\)(1)=5 and \( \beta_3\)(4)=6 (and reciprocally). This configuration is not possible in a quasi-manifold: two d-cells are always glue along an "entire" (d-1)-cells.
But as we can see in the second example (Right), the condition that all the darts of the cell are linked in not sufficient. Indeed, in this example, all the darts of the 2-cell between the cube and the pyramid are linked together by \( \beta_3\). However, this configuration does not correspond to an orientable 3D quasi-manifold. Indeed, the operation of gluing two d-cells along one (d-1)-cell must preserve the structure of the initial (d-1)-cell.
To avoid these two kinds of configurations, conditions are added on \( \beta\) pointers compositions (see Section Mathematical Definitions, condition (4) of the definition of combinatorial maps). Intuitively these conditions say that if two darts are linked by \( \beta_i\), then all the required darts are linked by \( \beta_i\) two by two in such a way that neighborhood relations are preserved.
We say that a combinatorial map is valid if it satisfies all the conditions on \( \beta\) pointers and on association between darts and attributes. High level operations provided on combinatorial maps ensure that these conditions are always satisfied. Sometimes, it can be useful to use low level operations in a specific algorithm, for example to modify locally a combinatorial map in a really fast way. In such a case, additional operations may be needed to restore these validity conditions.
The diagram in Figure 27.9 shows the different classes of the package. Combinatorial_map is the main class (see Section Combinatorial Maps). It allows to manage darts (see Section Darts) and attributes (see Section Cell Attributes). Users can customize a combinatorial map thanks to an items class (see Section Combinatorial Map Items), which defines the dart type and the attribute types. These types may be different for different dimensions, and they may also be void.
The darts and attributes are accessed through handles. A handle is a model of the Handle concept, thus supporting the two dereference operators operator* and operator->. All handles are model of LessThanComparable and Hashable, that is they can be used as keys in containers such as std::map and boost::unordered_map.
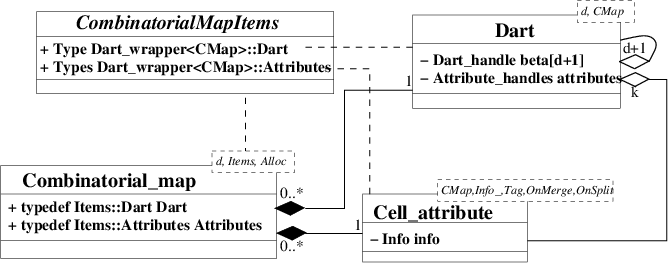
The class Combinatorial_map<d,Items,Alloc> is a model of the CombinatorialMap concept. It has three template parameters standing for the dimension of the combinatorial map (an unsigned int), an items class (a model of the CombinatorialMapItems concept), and an allocator which must be a model of the allocator concept of the STL. Default classes are provided for the items and the allocator classes.
The main role of the class Combinatorial_map is the storage and the management of darts. It allows to create or remove an isolated dart from the combinatorial map. The Dart_handle type defines a handle to the type of used darts (given in the items class). Combinatorial_map provides several ranges which allow to iterate over specific subsets of darts of the combinatorial map (see Section Iterating over Orbits, Cells, and Attributes). It also defines several methods to link and to unlink darts by \( \beta_i\)s (see Section Sewing Orbits and Linking Darts). We said that a dart d0 is i-free if \( \beta_i\)(d0)= \( \varnothing\). The \( \varnothing\) constant is represented in the class Combinatorial_map through a Dart_handle called null_dart_handle. Finally, some high level operations are defined as global functions taking a Combinatorial_map as argument (see Section Removal and Insertion Operations)
The second role of the class Combinatorial_map is the storage and the management of attributes. It allows to create or remove an attribute, and provides methods to associate attributes and cells. A range is defined for each i-attribute allowing to iterate over all the i-attributes of the combinatorial map. Finally, Combinatorial_map defines several types allowing to manage the attributes. We can use Combinatorial_map::Attribute_handle<i>::type for a handle to the i-attributes (and the const version Combinatorial_map::Attribute_const_handle<i>::type ) and Combinatorial_map::Attribute_type<i>::type for the type of the i-attributes.
All information associated to darts ( \( \beta\) links and attributes) can be accessed through member functions in CombinatorialMap.
The CombinatorialMapItems concept defines dart and attribute types of a combinatorial map. It contains one inner class named Dart_wrapper, having one template parameter, CMap, a model of CombinatorialMap concept. The Dart_wrapper<CMap> class provides two local types: Dart which must be a model of the Dart concept, and Attributes which defines the attributes and their types.
The Attributes tuple must contain at most d+1 types (one for each possible cell dimension of the combinatorial map). Each type of the tuple must be either a model of the CellAttribute concept or void. The first type corresponds to 0-attributes, the second to 1-attributes and so on. If the i th type in the tuple is void, (i-1)-attributes are disabled: we say that (i-1)-attributes are void. Otherwise, (i-1)-attributes are enabled and have the given type: we say (i-1)-attributes are non void. If the size of the tuple is k, with k \( <\)dimension+1, \( \forall\)i: k \( \leq\)i \( \leq\)dimension, i-attributes are void.
The class Combinatorial_map_min_items<d> is a model of the CombinatorialMapItems concept which can be used for default behaviors. It defines Dart<d,CMap> as type of dart, and Attributes as empty tuple.
The class Dart<d,CMap>, a model of the Dart concept, defines a dD dart. It has two template parameters standing for the dimension of the combinatorial map, and a model of the CombinatorialMap concept, which provides the two types Dart_handle and Dart_const_handle.
Each instance d0 of Dart<d,CMap> stores the \( \beta_i\) pointers in an array of d+1 Dart_handle (because we describe also the \( \beta_0\) pointer). It also stores the attributes associated to this dart in a tuple of CMap::Attribute_handle<i>::type , one for each non void i-attribute.
Methods are defined allowing to retrieve each \( \beta_i\) and each associated i-attribute of d0.
Note that the use of the Dart class is not hard wired in the combinatorial map class. Users can provide their own model of the Dart concept, and pass it to the combinatorial map with the help of a custom item class.
The class Cell_attribute<CMap,Info_,Tag,OnMerge,OnSplit>, a model of the CellAttribute concept, represents an attribute associated with a cell of a combinatorial map. The template parameter CMap must be a model of the CombinatorialMap concept. The attribute stores a handle to one dart of its associated cell when the template parameter Tag is Tag_true . Info_ is the type of information stored in the attribute. It may be void. OnMerge and OnSplit must be either Null_functor, or models of the Binary Function concept having two references to a model of CellAttribute as type of both parameters and void as return type. There are two default parameters for OnMerge and OnSplit, which are Null_functor, a default parameter for Tag which is Tag_true, and a default parameter for Info_ which is void.
If Info_ is different from void, the class Cell_attribute contains two methods info() returning the information contained in the attribute (const and non const version). The information is returned by reference, thus the non const version allows the modification of the information.
Two attributes are merged when their corresponding cells are merged into one cell during some operation. In this case, the functor OnMerge is called, unless it is equal to Null_functor. This functor allows the user to define its own custom behavior when two attributes are merged (for example if the information is a color, we can compute the average color of the two initial attributes, and affect this value to the first attribute, see example in Section Combinatorial Map With Attributes). Similarly, the functor OnSplit is called when one attribute is split in two, because its corresponding cell is split in two during some operation, unless it is equal to Null_functor. In any high level operation, OnMerge is called before to start the operation (i.e. before modifying the combinatorial map), and OnSplit is called when the operation is finished (i.e. after all the modifications were made).
In addition, there are dynamic onmerge and onsplit functions that can be associated to i-attributes, and modified, thanks to the onmerge_function() and onsplit_function(). When these functions are set, they are also called in addition to the previous mechanism when two attributes are merged or one attribute is split into two (see example in Section Use of Dynamic Onmerge and Onsplit Functors).
What we said for the dart also holds for the cell attribute. The combinatorial map can be used with any user defined model of the CellAttribute concept.
Here comes an example of two combinatorial map definitions. The first case Example_cmap4 defines a 4D combinatorial map which uses all the default values (Dart and Combinatorial_map_min_items). The second example Example_custom_cmap3 uses its own model of the CombinatorialMapItems concept. In this model, the type of dart is Dart<3,CMap>, thus a dart is in 3D, and an attribute containing an integer is associated to edges.
An important operation in combinatorial maps consists in iterating over specific subsets of darts or over attributes. For that, several ranges are offered (see Section Iterating over Orbits, Cells, and Attributes). A range is a model of the Range concept, thus supporting the two methods begin() and end() allowing to iterate over all the elements in the range. Several global functions allow to create specific configurations of darts into a combinatorial map (see Section Construction Operations). Darts can be marked during operations, for example when performing a breadth-first search traversal, thanks to Boolean marks (see Sections Boolean Marks). In the following, we denote by dh0, dh1, dh2 the dart handles for the darts d0, d1, d2, respectively. That is d0 == *dh0.
The combinatorial map offers iterators to traverse the darts of a specific orbit, to traverse all darts of one cell, or one dart per cell, and to traverse all i-attributes.
Instead of the begin()/end() member function pair as we know it from STL containers, and from most CGAL data structures, the combinatorial map defines range classes which are all models of the Range concept.
There are three different categories of dart range classes:
Dart_range: range of all the darts of a combinatorial map;
Dart_of_orbit_range<Beta...>: range of all the darts of the orbit \( \langle{}\)Beta... \( \rangle{}\)(d0) for a given d0. Beta... is a sequence of integers \( i_1\),..., \( i_k\), each \( i_j\) \( \in\){0, ..., d}. These integers must satisfy: \( i_1\) \( <\) \( i_2\) \( <\)... \( <\) \( i_k\), and ( \( i_1\) \( \neq\) 0 or \( i_2\) \( \neq\) 1) (for example Dart_of_orbit_range<1,2> for the orbit \( \langle{}\) \( \beta_1\), \( \beta_2\) \( \rangle{}\)(d0));
Dart_of_cell_range<i,dim>: range of all the darts of the i-cell containing a given dart. The i-cell is considered in dimension dim (with 0 \( \leq\)dim \( \leq\)d, dim=d by default), with 0 \( \leq\)i \( \leq\)dim+1. If i=dim+1, Dart_of_cell_range<i,dim> is the range of all the darts of the connected component containing a given dart. There are also two different classes of ranges containing one dart per i-cell. Note that in these classes, the dart of each i-cell can be any dart of the cell. Moreover, each i-cell (and j-cell in the second case) is considered in dimension dim (with 0 \( \leq\)dim \( \leq\)d, dim=d by default).
One_dart_per_cell_range<i,dim>: range containing one dart of each i-cell of the combinatorial map, 0 \( \leq\)i \( \leq\)dim+1 (for example One_dart_per_cell_range<2> for the range of one dart per 2-cell of the combinatorial map);
One_dart_per_incident_cell_range<i,j,dim>: range containing one dart of each i-cell incident to the j-cell containing a given dart, with 0 \( \leq\)i \( \leq\)dim+1 and 0 \( \leq\)j \( \leq\)dim+1 (for example One_dart_per_incident_cell_range<0,3> for the range of one dart per vertex of the volume incident to the starting dart). If i=j, the range contains only the given dart. The iterators of the Dart_range are bidirectional iterators, while the iterators of the other four ranges are forward iterators. The value type of all these iterators is Dart thus all these iterators can be directly used as Dart_handle.
Additionally, there is a range over non void i-attributes: Attribute_range<i>::type, having a bidirectional iterator with value type Attribute_type<i>::type`.
For each range, there is an associated const range, a model of the ConstRange concept. You can find some examples of ranges in Section A 3D Combinatorial Map.
Several global functions allow to create specific configurations of darts into a combinatorial map. Existing darts in the combinatorial map are not modified. Note that the dimension of the combinatorial map must be large enough: darts must contain all the \( \beta\) pointers used by the operation. All these functions take an instance of CombinatorialMap as first parameter (called cm) and return a Dart_handle to a new dart created during the operation.
make_edge<CMap>(cm): creates an isolated edge (two darts linked by \( \beta_2\)); dimension must be greater or equal than two; make_combinatorial_polygon<CMap>(cm,lg): creates an isolated combinatorial polygon of length lg (lg darts linked by \( \beta_1\)), for lg>0; dimension must be greater or equal than one; make_combinatorial_tetrahedron<CMap>(cm): creates an isolated combinatorial tetrahedron (four combinatorial triangles linked together by \( \beta_2\)); dimension must be greater or equal than two; make_combinatorial_hexahedron<CMap>(cm): creates an isolated combinatorial hexahedron (six combinatorial quadrangles linked together by \( \beta_2\)); dimension must be greater or equal than two. It is often necessary to mark darts, for example to retrieve in O(1) if a given dart was already processed during a specific algorithm, for example, iteration over a given range. Users can also mark specific parts of a combinatorial map (for example mark all the darts belonging to objects having specific semantics). To answer these needs, a CombinatorialMap has a certain number of Boolean marks (fixed by the constant NB_MARKS). When one wants to use a Boolean mark, the following methods are available (with cm an instance of a combinatorial map):
size_type m = cm.get_new_mark() (throws the exception Exception_no_more_available_mark if no mark is available); m for a given dart d0: cm.mark(dh0,m); m for a given dart d0: cm.unmark(dh0,m); d0 is marked for m: cm.is_marked(dh0,m); cm for m: cm.unmark_all(m); m of all the darts of cm: cm.negate_mark(m). All the marked darts become unmarked and all the unmarked darts become marked; m: cm.free_mark(m). This method unmarks all the darts of cm for m before freeing it. It is important to free a mark when it is no longer needed, otherwise you may at some point run out of marks.
The following example illustrates how to use marks. Two combinatorial tetrahedra are created and 3-sewn (see Section Sewing Orbits and Linking Darts for a detailed description of the sew operation). Then a mark is reserved and used to mark all the darts belonging to the first combinatorial tetrahedron. Finally, these tetrahedron are merged. The marks allow us to know which darts come from the first and second tetrahedron.
File Combinatorial_map/map_3_marks.cpp
Several operations allow to modify a given combinatorial map. There are two main categories of modification operations:
The CombinatorialMap defines two groups of methods to modify the \( \beta\) pointers of existing darts.
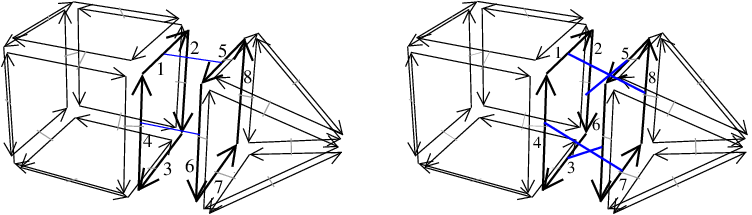
The sew and unsew methods iterate over two orbits in order to link or unlink specific darts two by two. Intuitively, a sew<i> operation glues two i-cells by identifying two of their (i-1)-cells (see example in Figure 27.10 where sew<3> is used to glue two 3-cells along one 2-cell). Reciprocally, a unsew<i> operation un-glues two i-cells which were glued along one of their (i-1)-cells. These methods guarantee that given a valid combinatorial map and a possible operation we obtain a valid combinatorial map as result of the operation.
The link_beta and unlink_beta methods only modify the pointer of two darts: the obtained combinatorial maps may be not valid. These operations can be useful to use low level operations in a specific algorithm, for example to modify locally a combinatorial map in a really fast way. In such a case, additional operations may be needed to restore the validity conditions.
Linking two darts d1 and d2 by \( \beta_i\), with 2 \( \leq\)i \( \leq\)d and d1 \( \neq\)d2, consists in modifying two \( \beta_i\) pointers such that \( \beta_i\)(d1)=d2 and \( \beta_i\)(d2)=d1. For i=1, the modification is \( \beta_1\)(d1)=d2 (and thus \( \beta_0\)(d2)=d1 by definition of \( \beta_0\)); in this case we can have d1=d2 (a dart linked with itself corresponds to an edge which is a loop).
Reciprocally, unlinking a given dart d0 by \( \beta_i\), with 2 \( \leq\) i \( \leq\)d, consists in modifying two \( \beta_i\) pointers such that \( \beta_i\)( \( \beta_i\)(d0))= \( \varnothing\) and \( \beta_i\)(d0)= \( \varnothing\). For i=1, the modification is \( \beta_1\)(d0)= \( \varnothing\) (and thus \( \beta_0\)( \( \beta_1\)(d0))= \( \varnothing\) by definition of \( \beta_0\)). Note that is it possible to unlink a given dart for \( \beta_i\) only if it is not i-free.
The sew<i>(dh1,dh2) method consists mainly to link two by two several darts by \( \beta_i\). This operation is possible only if there is a bijection f between all the darts of the orbit D1= \( \langle{}\) \( \beta_1\),..., \( \beta_{i-2}\), \( \beta_{i+2}\),..., \( \beta_d\) \( \rangle{}\)(d1) and D2= \( \langle{}\) \( \beta_1\),..., \( \beta_{i-2}\), \( \beta_{i+2}\),..., \( \beta_d\) \( \rangle{}\)(d2) satisfying: f(d1)=d2, and for all e \( \in\)D1, for all j \( \in\){1,..., i-2,i+2,...,d}, f( \( \beta_j\)(e))= \( \beta_j^{-1}\)(f(e)). Intuitively, this condition ensures the validity of the combinatorial map by verifying that condition discussed in Section Combinatorial Map Properties will be satisfied after the operation. This condition can be tested by using the method is_sewable<i>(dh1,dh2). For example, the function is_sewable<3> would return false if we tried to 3-sew a triangular facet with a quad facet. Note that given two darts d1 and d2, if there is such a bijection, it is uniquely defined. So giving the two darts as arguments of the sew<i> is enough to retrieve all the pairs of darts to link. If such a bijection exists, the sew<i>(dh1,dh2) operation consists only in linking by \( \beta_i\) each couple of darts d3 and d4 such that d3=f(d4).
In addition, the sew operation updates the associations between darts and non void attributes in order to guarantee that all the darts belonging to a given cell are associated with the same attribute (which is a condition of combinatorial map validity). For each couple of j-cells c1 and c2 that are merged into one j-cell during the sew, we have to update the two associated attributes attr1 and attr2. If both are NULL, there is nothing to do. If one is NULL and the other not, we only associate the non NULL attribute to all the darts of the resulting cell. When the two attributes are non NULL, we first apply functor On_merge on the two attributes attr1 and attr2 (see Section Cell Attributes). Then, we associate the attribute attr1 to all darts of the resulting j-cell. Finally, attribute attr2 is removed from the combinatorial map.
Note that when the two attributes are non NULL, the first one is kept. But user can customize this behavior in order to update the information contained in the attributes according to its needs. For that, we can define a specific functor, and use it as template argument for On_merge parameter of the Cell_attribute definition. This functor can for example copy the information of the second attribute in the information of the first one to make as if the second attribute is kept.
For example, in Figure 27.10, we want to 3-sew the two initial volumes. sew<3>(1,5) links by \( \beta_3\) the pairs of darts (1,5), (2,8), (3,7) and (4,6), thus the combinatorial map obtained is valid. 2-attributes are updated so that all the darts belonging to the 2-cell containing dart 1 become associated to the same 2-attribute after the operation.
Similarly, unsew<i>(dh0) operation unlinks \( \beta_i\) for all the darts in the orbit \( \langle{}\) \( \beta_1\),..., \( \beta_{i-2}\), \( \beta_{i+2}\),..., \( \beta_d\) \( \rangle{}\)(d0), and thus guarantees to obtain a valid combinatorial map. This operation is possible for any non i-free dart.
As for the sew operations, attributes are updated to guarantee that two darts belonging to two different j-cells are associated to two different j-attributes. If the unsew operation splits a j-cell c in two j-cells c1 and c2, and if c is associated to a j-attribute attr1, then this attribute is duplicated into attr2, and all the darts belonging to c2 are associated with this new attribute. Finally, we call the functor On_split on the two attributes attr1 and attr2 (see Section Cell Attributes).
Let us consider the combinatorial map given in Figure 27.10 (Right). If we call unsew<3>(2), we obtain the combinatorial map in Figure 27.10 (Left) (except for the color of the attribute associated to the 2-cell {5,6,7,8} which would be #00ff00). The unsew<3> operation has duplicated the 2-attribute associated to the 2-cell {1,2,3,4,5,6,7,8} since this 2-cell is split in two after the unsew operation.
If one wants to modify a combinatorial map manually, it is possible to switch off the updating between darts and attributes by calling set_automatic_attributes_management(false) before to call sew<i>(dh1,dh2) and unsew<i>(dh0). In these cases, the combinatorial map obtained may be no longer valid due to incorrect associations between darts and attributes. In Figure 27.10 (Left), if we call sew<3>(1,5), the resulting combinatorial map is similar to the combinatorial map of Figure 27.10 (Right) (we have linked by \( \beta_3\) the pairs of darts (1,5), (2,8), (3,7) and (4,6)), but associations between darts and attributes are not valid. Indeed, we have kept the four initial attributes and all the associations between darts and attributes, thus two darts belonging to the same 2-cell (for example darts 1 and 5) are associated with two different attributes. We can also use the link_beta<i>(dh1,dh2) which links d1 and d2 by \( \beta_i\) without modifying the other links. Association between darts and attributes are only modified for darts d1 and d2, and similarly as for sew<i>, this updating can be avoided by calling set_automatic_attributes_management(false) before to call link_beta<i>(dh1,dh2). Lastly, we can use unlink_beta<i>(dh0) to unlink d0 for \( \beta_i\). In this last case, there is no modification of association between darts and attributes. In Figure 27.10 (Left), if we call link_beta<3>(1,5), in the resulting combinatorial map we have now \( \beta_3\)(1)=5 and \( \beta_3\)(5)=1. This combinatorial map is no longer valid (for example dart 2 is 3-free and we should have \( \beta_3\)(2)=8). A call latter to set_automatic_attributes_management(true) will correct the invalid non void attributes.
The following high level operations are defined as global functions taking an instance cm of CombinatorialMap as first argument. All these methods ensure that given a valid combinatorial map and a possible operation, the modified combinatorial map is also valid.
The first one is remove_cell<CMap,i>(cm,dh0) which modifies the combinatorial map to remove the i-cell containing dart d0, with 0 \( \leq\)i \( \leq\)d. This operation is possible if i=d or if the given i-cell is incident to at most two (i+1)-cells which can be tested thanks to is_removable<CMap,i>(cm,dh0). If the removed i-cell was incident to two different (i+1)-cells, these two cells are merged into one (i+1)-cell. In this case, the On_merge functor is called if two (i+1)-attributes are associated to the two (i+1)-cells. If the i-cell is associated with a non void attribute, it is removed from the combinatorial map (see three examples on Figure 27.11, Figure 27.13 and Figure 27.14).
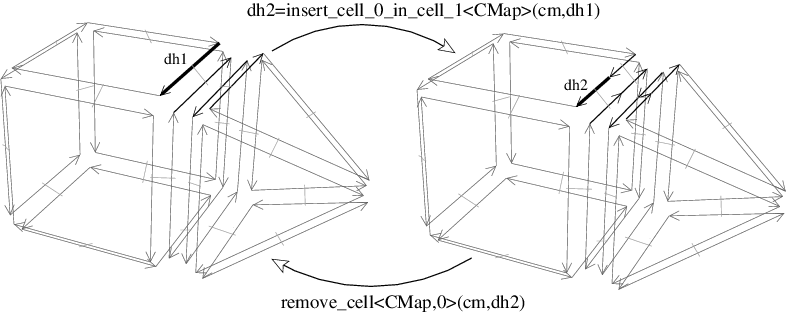
insert_cell_0_in_cell_1 and remove_cell<0> operations. Left: Initial combinatorial map. Right: After the insertion of a 0-cell in the 1-cell containing dart d1. Now if we remove the 0-cell containing dart d2, we obtain the initial combinatorial map. The inverse operation of the removal is the insertion operation. Several versions exist, sharing a common principle. They consist in adding a new i-cell "inside" an existing j-cell, i \( <\)j, by splitting the j-cell into several j-cells. Contrary to remove_cell<CMap,i>, is it not possible to define a unique insert_cell_i_in_cell_j<CMap,i,j> function because parameters are different depending on i and j.
insert_cell_0_in_cell_1<CMap>(cm,dh0) adds a 0-cell in the 1-cell containing dart d0. The 1-cell is split in two. This operation is possible if d0 \( \in\)cm.darts() (see example on Figure 27.11).
insert_cell_0_in_cell_2<CMap>(cm,dh0) adds a 0-cell in the 2-cell containing dart d0. The 2-cell is split in triangles, one for each initial edge of the facet. This operation is possible if d0 \( \in\)cm.darts() (see example on Figure 27.12).
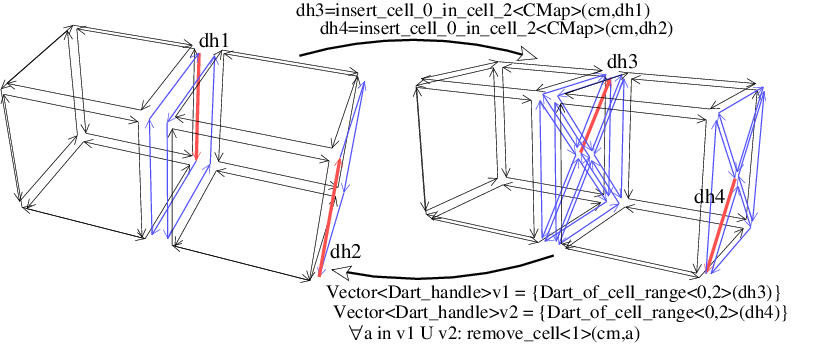
insert_cell_0_in_cell_2 operation. insert_cell_1_in_cell_2<CMap>(cm,dh1,dh2) adds a 1-cell in the 2-cell containing darts d1 and d2, between the two 0-cells containing darts d1 and d2. The 2-cell is split in two. This operation is possible if d1 \( \in\) \( \langle{}\) \( \beta_1\) \( \rangle{}\)(d2) which can be tested thanks to is_insertable_cell_1_in_cell_2<CMap>(cm,dh1,dh2). In the example on Figure 27.13, it is possible to insert an edge between darts d2 and d3, but it is not possible to insert an edge between d1 and d3.

insert_cell_1_in_cell_2 and remove_cell<1> operations. Left: Initial combinatorial map. Right: After the insertion of two 1-cells: a first one between the two 0-cells containing darts d2 and d3, and a second one incident to the 0-cell containing dart d1. Now if we remove the two 1-cells containing darts d4 and d5, we obtain the initial combinatorial map. insert_dangling_cell_1_in_cell_2<CMap>(cm,dh0) adds a 1-cell in the 2-cell containing dart d0, the 1-cell being attached by only one of its vertex to the 0-cell containing dart d0. This operation is possible if d0 \( \in\)cm.darts().
insert_cell_2_in_cell_3<CMap>(cm,itbegin,itend) adds a 2-cell in the 3-cell containing all the darts between itbegin and itend, along the path of 1-cells containing darts in [itbegin,itend). The 3-cell is split in two. This operation is possible if all the darts in [itbegin,itend) form a closed path inside a same 3-cell which can be tested thanks to is_insertable_cell_2_in_cell_3<CMap>(cm,itbegin,itend) (see example on Figure 27.14).
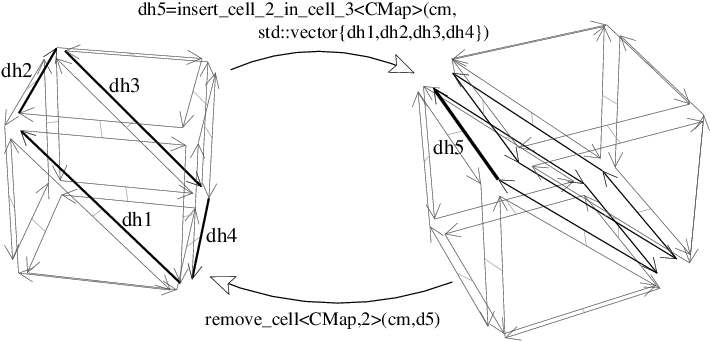
insert_cell_2_in_cell_3 and remove_cell<2> operations. Left: Initial combinatorial map. Right: After the insertion of a 2-cell along the path of 1-cells containing respectively d1,d2,d3,d4. Now if we remove the 2-cell containing dart d5, we obtain the initial combinatorial map. Some examples of use of these operations are given in Section High Level Operations.
If set_automatic_attributes_management(false) is called, all the future insertion or removal operations will not update non void attributes. These attributes will be updated latter by the call to set_automatic_attributes_management(true). This can be useful to speed up an algorithm which uses several successive insertion and removal operations. See example Automatic attributes management.
In this example, a 3-dimensional combinatorial map is constructed. Two combinatorial tetrahedra are created, then the numbers of cells of the combinatorial map are displayed, and the validity of the combinatorial map is checked. Then, we illustrate the use of ranges to iterate over specific darts. The first loop enumerates all the darts of the first tetrahedron by using the range Dart_of_orbit_range<1,2>, and the second loop enumerates all the darts of the facet containing dart dh2 by using the range Dart_of_orbit_range<1>.
File Combinatorial_map/map_3_simple_example.cpp
The output is:
#Darts=24, #0-cells=8, #1-cells=12, #2-cells=8, #3-cells=2, #ccs=2, valid=1 Number of darts of the first tetrahedron: 12 Number of darts of the facet containing dh2: 3
which gives the number of darts of the combinatorial map, the numbers of different cells, the number of connected components, and finally a Boolean showing the validity of the combinatorial map (a tetrahedron is made up of 12 darts because there are 3 darts per facet and there are 4 facets).
Note the creation in the for loops of the two instances of Dart_of_orbit_range::const_iterator: it is the current iterator, and itend an iterator to the end of the range. Having itend avoids calling cm.darts_of_orbit<1,2>(dh1).end() again and again as in the following example (which is a bad solution):
This example shows some uses of high level operations. First we create a combinatorial hexahedron, the combinatorial map obtained is shown in Figure 27.15 (Left). Then we insert two 1-cells along two opposite 2-cells of the hexahedron. The combinatorial map obtained is shown in Figure 27.15 (Middle). Finally, we insert a 2-cell in the diagonal of the hexahedron in order to split it into two parts. We obtain the combinatorial map shown in Figure 27.15 (Right). We display the characteristics of the combinatorial map and check its validity.
The second part of this example removes the inserted elements. First we remove the inserted 2-cell, then the two inserted 1-cells. We get back the initial combinatorial hexahedron, which is verified by displaying once again the characteristics of the combinatorial map.
File Combinatorial_map/map_3_operations.cpp
The output is:
#Darts=36, #0-cells=8, #1-cells=14, #2-cells=9, #3-cells=2, #ccs=1, valid=1 #Darts=24, #0-cells=8, #1-cells=12, #2-cells=6, #3-cells=1, #ccs=1, valid=1
The first line gives the characteristics of the combinatorial map after all the insertions (the combinatorial map drawn in Figure 27.15 (Right)). There are two 3-cells (since the combinatorial hexahedron was split in two by the 2-cell insertion), nine 2-cells (since two 2-cells of the original hexahedron were split in two by the two 1-cell insertions, and a new 2-cell was created during the 2-cell insertion), fourteen 1-cells (since there are two new 1-cells created by the 1-cell insertion) while the number of 0-cells remains unchanged.
The second line is the result after the removal operations. We retrieve the original combinatorial hexahedron since we have removed all the inserted elements.
In this example, a 4-dimensional combinatorial map is used. Two tetrahedral cells are created and sewn by \( \beta_4\). Then the numbers of cells of the combinatorial map are displayed, and its validity is checked.
By looking at these numbers of cells, we can see that the 4D combinatorial map contains only one 3-cell. Indeed, the sew<4> operation has identified by pairs all the darts of the two 3-cells by definition of the sew operation (see Section Sewing Orbits and Linking Darts) which, in 4D, links by \( \beta_3\) all the darts in \( \langle{}\) \( \beta_1\), \( \beta_2\) \( \rangle{}\)(d1) and in \( \langle{}\) \( \beta_1\), \( \beta_2\) \( \rangle{}\)(d2). The situation is similar (but in higher dimension) to the configuration where we have two triangles in a 3D combinatorial map, and you use sew<3> between these two triangles. The two triangles are identified since all their darts are linked by \( \beta_3\), thus we obtain a 3D combinatorial map containing only one 3-cell. Note that this 3-cell is unbounded since the darts of the two triangles are all 2-free. In the 4D case, the 4-cell is unbounded since all its darts are 3-free.
In this example, we also illustrate how to use the basic methods to build "by hand" some specific configuration in a combinatorial map. In fact, these functions are already present in the package: function make_triangle(cm) is equivalent to make_combinatorial_polygon(cm,3) and make_tetrahedral(cm) is equivalent to make_combinatorial_tetrahedron(cm). If we want to create a 4D simplex, we must create five 3D simplexes, and sew them correctly two by two by \( \beta_3\) (and so on if you want to create higher dimensional combinatorial map).
File Combinatorial_map/map_4_simple_example.cpp
The output is:
#Darts=24, #0-cells=4, #1-cells=6, #2-cells=4, #3-cells=1, #4-cells=2, #ccs=1, valid=1
In the following example, we illustrate how to specify the 2-attributes in a 3D combinatorial map. For that, we define our own item class using Dart<3,CMap> as type of dart, and Cell_attribute<CMap,int,Tag_true,Sum_functor,Divide_by_two_functor> as attributes which contain an int and which are associated to 2-cells of the combinatorial map.
Functors Sum_functor and Divide_by_two_functor define a custom behavior: when two attributes ca1 and ca2 are merged into ca1, the value of ca1 is the sum of the two initial values. When an attribute ca1 is split in the two attributes ca1 and ca2, the value of each attribute is half of the first value.
File Combinatorial_map/map_3_with_colored_facets.cpp
The output is:
20; 7; 7; 7; 7; 7; 13; 13; 13; 13; 13; 2; 7; 7; 7; 7; 7; 2; 13; 13; 13; 13; 13; 5; 10; #Darts=64, #0-cells=13, #1-cells=24, #2-cells=14, #3-cells=2, #ccs=1, valid=1
Before the cm.sew<3>, each 2-cell of the first cube is associated with an attribute having 7 as value, and each 2-cell of the second cube with an attribute having 13 as value. During the cm.sew<3>, two 2-cells are merged, thus the functor Sum_functor is called on the two associated 2-attributes, and the value of the new 2-cell is the sum of the two previous one: 20.
Then we call insert_cell_0_in_cell_2 on a dart which belong to this 2-cell. This method splits the existing 2-cell in k 2-cells, k being the number of 1-cells of the initial 2-cell (4 in this example). These splits are made consecutively, thus for the first split, we create a new attribute as copy of the initial one and call functor Divide_by_two_functor on these two attributes: the value of each attribute is thus 20/2=10. For the second split, the value of each attribute is thus 10/2=5, and for the last split the value of each attribute is thus 5/2=2 (remember that information contained in 2-attributes in an int). At the end, we obtain five 2-attributes with 7 as value, five 2-attributes with 13 as value, and four 2-attributes having respectively 2, 2, 5 and 10 as values.
In the following example, we show an example of use of dynamic onmerge and onsplit functor. We define our 3D combinatorial map with 2-attributes. Then we create two hexahedra and create all the 2-attributes. We initialize the info of the faces of the first hexahedron to 7 and the info of the faces of the second hexahedron to 13.
Step 3 defines the onsplit and onmerge dynamic functors. We can see here that with this mechanism, functors can store data member. This is the case in the example for Split_functor which stores a reference to the combinatorial map.
The next operations will call these functors when 2-cells are split or merged. The sew<3> operation calls 1 onmerge as two faces are identified; the insert_cell_0_in_cell_2 operation calls 4 onsplit as one face is split in 4.
Lastly we remove the dynamic onmerge functor (step 8). This is done by initializing the fonctor to a default boost::function. After this initialization, no dynamic merge functor is called when two faces are merged.
File Combinatorial_map/map_3_dynamic_onmerge.cpp
The initial definition of combinatorial map in any dimension is given in [2], [3]. But it allows only to represent objects without boundaries. This definition was extended [4], [1] in order to allow to represent objects with boundaries, based on the notions of partial permutations and partial involutions.
Intuitively, a partial permutation on a finite set E is a mapping from E \( \cup\{\varnothing\}\) to E \( \cup\{\varnothing\}\) which is injective on the subset of the domain that does not map to \(\varnothing\). More precisely, a mapping p: E \( \cup\{\varnothing\} \rightarrow\) E \( \cup\{\varnothing\}\) is a partial permutation defined on E if:
The inverse \( p^{-1}\) of this partial permutation is also a partial permutation and is defined by:
Let E be a set, and p a partial permutation on E. An element e is called a fixed point for p if p(e)=e. p is a partial involution if \( \forall\)e \( \in\)E: p(e) \( \neq\) \( \varnothing\) \( \Rightarrow\) p(p(e))=e.
Now we can give the definition of a combinatorial map in any dimension. Let d \( \geq\) 0. A d-dimensional combinatorial map (or d-map) is a (d+1)-tuple M=(D, \( \beta_1\),..., \( \beta_d\)) where:
A d-dimensional combinatorial map represents a subdivision of an orientable d-dimensional quasi-manifold. A dart is an abstract element which is only required to define partial permutations. The last line of the definition fixes constraints which guarantee the topological validity of the represented object, i.e., the fact that it is a quasi-manifold. This definition allows us to verify the validity of a given combinatorial map by checking if each item of the definition is satisfied.
Given a set of partial permutations S= \(\{f_1\),..., \( f_k\}\), we denote by \( \langle{}\) S \( \rangle{}\) the permutation group generated by \(\{f_1\),..., \( f_k\}\) and whose group operation is the composition of partial permutations. The orbit \( \langle{}\) \( f_1\),..., \( f_k\) \( \rangle{}\)(a) is the set of darts which can be obtained from a by elements of \( \langle{}\) S \( \rangle{}\): \( \langle{}\) \( f_1\),..., \( f_k\) \( \rangle{}\)(a)= \(\{ \phi\)(a) \( |\) \( \phi\) \( \in\) \( \langle{}\)S \( \rangle{}\}\setminus\{\varnothing\}\).
Let d0 \( \in\)D be a dart. Given i, 1 \( \leq\)i \( \leq\)d, the i-cell containing d0 is \( \langle{}\) \( \beta_1\),..., \( \beta_{i-1}\), \( \beta_{i+1}\),..., \( \beta_d\) \( \rangle{}\)(d0). The 0-cell containing d0 is \( \langle{}\){ \( \beta_i\) \( \circ\) \( \beta_j\) \( |\) \( \forall\)i,j: 1 \( \leq\)i \( <\)j \( \leq\)d} \( \rangle{}\)(d0).
The code of this package is inspired by Moka, a 3D topological modeler mainly developed by Frédéric Vidil and Guillaume Damiand (http://moka-modeller.sourceforge.net/). However, Moka was based on Generalized maps (and not Combinatorial maps), and the design was not CGAL "compatible". Thus, Guillaume Damiand started to develop a totally new package by mixing ideas taken from Moka with the design of the Halfedge data structure package of CGAL. Andreas Fabri and Sébastien Loriot contributed to the design, the coding, and to the documentation of the package, and Laurent Rineau helped for the design. Emma Michel contributed to the manual. Monique Teillaud and Bernd Gärtner contributed to the manual by giving useful remarks, really numerous and detailed for Monique. Ken Arroyo Ohori contributed to the two reverse orientation functions.