\( \newcommand{\E}{\mathrm{E}} \) \( \newcommand{\A}{\mathrm{A}} \) \( \newcommand{\R}{\mathrm{R}} \) \( \newcommand{\N}{\mathrm{N}} \) \( \newcommand{\Q}{\mathrm{Q}} \) \( \newcommand{\Z}{\mathrm{Z}} \) \( \def\ccSum #1#2#3{ \sum_{#1}^{#2}{#3} } \def\ccProd #1#2#3{ \sum_{#1}^{#2}{#3} }\)
CGAL 4.8.2 - 3D Surface Subdivision Methods
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Groups Pages
Functions
Subdivision Methods
3D Surface Subdivision Methods

A subdivision method recursively refines a coarse mesh and generates an ever closer approximation to a smooth surface.

Subdivision_method_3 consists of four subdivision methods and their refinement hosts. Each refinement host is a template function of a polyhedron class and a geometry policy class. It refines the connectivity of the control mesh and computes the geometry of the refined mesh. The geometry computation is dedicated to the custom geometry policy. A geometry policy consists of functions that compute the new point based on the subdivision stencil. A stencil defines the footprint (a submesh of the control mesh) of a new point.

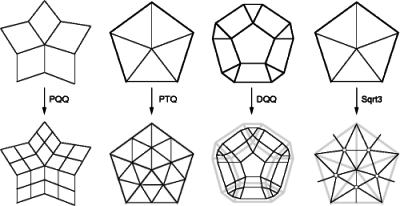
The four supported refinement hosts are the primal quadrilateral quadrisection (PQQ), the primal triangle quadrisection (PTQ), the dual quadrilateral quadrisection (DQQ), and the \( \sqrt{3}\) triangulation. These refinements are respectively used in Catmull-Clark, Loop, Doo-Sabin and \( \sqrt{3}\) subdivision.

Refinement Host

A refinement host is a template function of a polyhedron class and a geometry mask class. It refines the input polyhedron, and computes new points through the geometry masks. Subdivision_method_3 supports four refinement hosts: PQQ, PTQ, DQQ and Sqrt3.

RefSchemes.png

Example

This example program subdivides a polyhedral mesh with Catmull-Clark subdivision.


File Subdivision_method_3/CatmullClark_subdivision.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Subdivision_method_3.h>
#include <iostream>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
typedef CGAL::Simple_cartesian<double> Kernel;
typedef CGAL::Polyhedron_3<Kernel> Polyhedron;
using namespace std;
using namespace CGAL;
int main(int argc, char** argv) {
if (argc != 2) {
cout << "Usage: CatmullClark_subdivision d < filename" << endl;
cout << " d: the depth of the subdivision (0 < d < 10)" << endl;
cout << " filename: the input mesh (.off)" << endl;
return 0;
}
int d = argv[1][0] - '0';
Polyhedron P;
cin >> P; // read the .off
Subdivision_method_3::CatmullClark_subdivision(P,d);
cout << P; // write the .off
return 0;
}
See Also
CGAL::CatmullClark_mask_3<Polyhedron_3>
CGAL::Loop_mask_3<Polyhedron_3>
CGAL::Sqrt3_mask_3<Polyhedron_3>

Functions

template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::PQQ (Polyhedron_3 &p, Mask< Polyhedron_3 > mask, int step=1)
 applies the PQQ refinement on the control mesh p step times. More...
 
template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::PTQ (Polyhedron_3 &p, Mask< Polyhedron_3 > mask, int step=1)
 applies the PTQ refinement on the control mesh p step times, where p contains only triangle facets. More...
 
template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::DQQ (Polyhedron_3 &p, Mask< Polyhedron_3 > mask, int step=1)
 applies the DQQ refinement on the control mesh p step times. More...
 
template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::Sqrt3 (Polyhedron_3 &p, Mask< Polyhedron_3 > mask, int step=1)
 applies the \( \sqrt{3}\) triangulation on the control mesh p step times, where p contains only triangle facets. More...
 
template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::CatmullClark_subdivision (Polyhedron_3 &p, int step=1)
 applies Catmull-Clark subdivision step times on the control mesh p. More...
 
template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::Loop_subdivision (Polyhedron_3 &p, int step=1)
 applies Loop subdivision step times on the control mesh p. More...
 
template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::DooSabin_subdivision (Polyhedron_3 &p, int step=1)
 applies Doo-Sabin subdivision step times on the control mesh p. More...
 
template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::Sqrt3_subdivision (Polyhedron_3 &p, int step=1)
 applies \( \sqrt{3}\) subdivision step times on the control mesh p. More...
 

Function Documentation

template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::CatmullClark_subdivision ( Polyhedron_3 &  p,
int  step = 1 
)

applies Catmull-Clark subdivision step times on the control mesh p.

This function overwrites the control mesh p with the subdivided mesh.

#include <CGAL/Subdivision_method_3.h>

Examples:
Subdivision_method_3/CatmullClark_subdivision.cpp.
template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::DooSabin_subdivision ( Polyhedron_3 &  p,
int  step = 1 
)

applies Doo-Sabin subdivision step times on the control mesh p.

This function overwrites the control mesh p with the subdivided mesh.

#include <CGAL/Subdivision_method_3.h>

Examples:
Subdivision_method_3/DooSabin_subdivision.cpp.
template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::DQQ ( Polyhedron_3 &  p,
Mask< Polyhedron_3 >  mask,
int  step = 1 
)

applies the DQQ refinement on the control mesh p step times.

The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh.

#include <CGAL/Subdivision_method_3.h>

template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::Loop_subdivision ( Polyhedron_3 &  p,
int  step = 1 
)

applies Loop subdivision step times on the control mesh p.

This function overwrites the control mesh p with the subdivided mesh.

#include <CGAL/Subdivision_method_3.h>

template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::PQQ ( Polyhedron_3 &  p,
Mask< Polyhedron_3 >  mask,
int  step = 1 
)

applies the PQQ refinement on the control mesh p step times.

The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh.

#include <CGAL/Subdivision_method_3.h>

template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::PTQ ( Polyhedron_3 &  p,
Mask< Polyhedron_3 >  mask,
int  step = 1 
)

applies the PTQ refinement on the control mesh p step times, where p contains only triangle facets.

The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined.

#include <CGAL/Subdivision_method_3.h>

Examples:
Subdivision_method_3/Customized_subdivision.cpp.
template<class Polyhedron_3 , template< typename > class Mask>
void CGAL::Subdivision_method_3::Sqrt3 ( Polyhedron_3 &  p,
Mask< Polyhedron_3 >  mask,
int  step = 1 
)

applies the \( \sqrt{3}\) triangulation on the control mesh p step times, where p contains only triangle facets.

The geometry of the refined mesh is computed by the geometry policy mask. This function overwrites the control mesh p with the refined mesh. The result of a non-triangle mesh p is undefined.

#include <CGAL/Subdivision_method_3.h>

template<class Polyhedron_3 >
void CGAL::Subdivision_method_3::Sqrt3_subdivision ( Polyhedron_3 &  p,
int  step = 1 
)

applies \( \sqrt{3}\) subdivision step times on the control mesh p.

This function overwrites the control mesh p with the subdivided mesh.

#include <CGAL/Subdivision_method_3.h>