|
CGAL 4.9.1 - Convex Decomposition of Polyhedra
|
|
CGAL 4.9.1 - Convex Decomposition of Polyhedra
|
For many applications on non-convex polyhedra, there are efficient solutions that first decompose the polyhedron into convex pieces. As an example, the Minkowski sum of two polyhedra can be computed by decomposing both polyhedra into convex pieces, compute pair-wise Minkowski sums of the convex pieces, and unite the pair-wise sums.
While it is desirable to have a decomposition into a minimum number of pieces, this problem is known to be NP-hard [1]. Our implementation decomposes a Nef polyhedron \( N\) into \( O(r^2)\) convex pieces, where \( r\) is the number of edges that have two adjacent facets that span an angle of more than 180 degrees with respect to the interior of the polyhedron. Those edges are also called reflex edges. The bound of \( O(r^2)\) convex pieces is worst-case optimal [1].
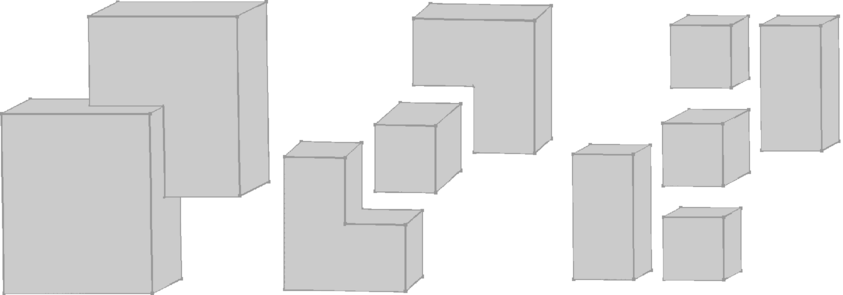
Our decomposition runs in two steps. In the first step, each non-vertical reflex edge \( e\) is resolved by insertion of vertical facets through \( e\). In the second step, we do the same with the vertical reflex edges. Figure 30.1 illustrates the two steps.
At the moment our implementation is restricted to the decomposition of bounded polyhedra. An extension to unbounded polyhedra is planned.
An instance of Nef_polyhedron_3 represents a subdivision of the three-dimensional space into vertices, edges, facets, and volumes. Some of these items form the polyhedron (selected), while others represent the outer volume or holes within the polyhedron (unselected). As an example, the unit cube is the point set \( [0,1]^3\). The smallest subdivision that represents the unit cube has 8 vertices, 12 edges, 6 facets, and 2 volumes. The volumes enclosed by the vertices, edges, and facets is the interior of the cube and therefore selected. The volume outside the cube does not belong to it and is therefore unselected. The vertices, edges, and facets - also denoted as boundary items - are needed to separate the two volumes, but are also useful for representing topological properties. In case of the (closed) unit cube the boundary items are part of the polyhedron and therefore selected, but in case of the open unit cube \( [0,1)^3\) they are unselected. Each item has its own selection mark, which allows the correct representation of Nef polyhedra, which are closed under Boolean and topological operations. Details can be found in Chapter 3D Boolean Operations on Nef Polyhedra.
Usually, an instance of Nef_polyhedron_3 does not contain any redundant items. However, the function convex_decomposition_3() subdivides selected volumes of a given Nef_polyhedron_3 by selected facets. These additional facets are therefore redundant, i.e., their insertion alters the representation of the polyhedron, but not the polyhedron itself.
When convex_decomposition_3() resolved all reflex edges, the selected sub-volumes have become convex. Each of them is represented by a separate volume item and can therefore be traversed separately as described in Section Exploring Shells. Another possibility of accessing the convex pieces is to convert them into separate Nef polyhedra, as illustrated by the example code given below.
Note that due to the restriction to bounded polyhedra, the use of extended kernels is unnecessary and expensive. We therefore do not support the use of extended kernels in the convex decomposition.
File Convex_decomposition_3/list_of_convex_parts.cpp