|
CGAL 4.9.1 - 2D Boolean Operations on Nef Polygons Embedded on the Sphere
|
|
CGAL 4.9.1 - 2D Boolean Operations on Nef Polygons Embedded on the Sphere
|
#include <CGAL/Nef_polyhedron_S2.h>
A sloop is a great circle on a sphere.
A shalfloop is an oriented sloop. It is always paired with a shalfloop whose supporting Sphere_circle is pointing in the opposite direction. The twin() member function returns this shalfloop of opposite orientation. Each Nef_polyhedron_S2 can only have one sloop (resp. two shalfloops).
The figure below depicts the relationship between a shalfloop and sfaces on a sphere map.
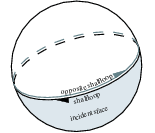
There is no need for a user to create a SHalfloop explicitly. The class Nef_polyhedron_S2<Traits> manages the needed shalfloops internally.
Types | |
The following types are the same as in | |
| typedef unspecified_type | Mark |
| type of mark. | |
| typedef unspecified_type | Sphere_circle |
| sphere circle type stored in SHalfloop. | |
| typedef unspecified_type | SHalfloop_const_handle |
| const handle to SHalfloop. | |
| typedef unspecified_type | SFace_const_handle |
| const handle to SFace. | |
Operations | |
| const Mark & | mark () const |
| the mark of the halfloop. | |
| const Sphere_circle & | circle () const |
| the sphere circle of the halfloop. | |
| SHalfloop_const_handle | twin () const |
| the twin of the halfloop. | |
| SFace_const_handle | incident_sface () const |
| the incident sface of the halfloop. | |