|
CGAL 4.9.1 - Triangulated Surface Mesh Simplification
|
|
CGAL 4.9.1 - Triangulated Surface Mesh Simplification
|
The concept EdgeCollapsableSurfaceMeshWithConstraints describes additional requirements for the type of triangulated surface meshes that can be passed to the simplification algorithm.
Valid Expressions
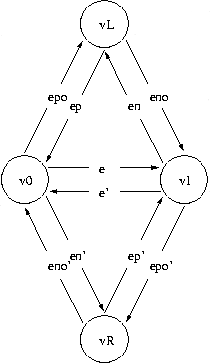
Let v0v1 be an edge of the triangulated surface mesh ecm and v0 and v1 being the source and target vertices of that edge. The surface mesh simplification algorithm requires the call to the function halfedge_collapse(v0v1,ecm) to be valid and to return the vertex not removed after collapsing the undirected edge (v0v1,v1v0).
For e \( \in \{\) v0v1,v1v0 \( \}\), let en and ep be the next and previous edges, that is en = next_edge(e, surface_mesh), ep = prev_edge(e,surface_mesh), and let eno and epo be their opposite edges, that is eno = opposite_edge(en, surface_mesh) and epo = opposite_edge(ep,surface_mesh).
Then, after the collapse of (v0v1,v1v0) the invariants described in the concept EdgeCollapsableSurfaceMesh hold if ep is not constrained. Otherwise, it is en that is removed from ecm.
CGAL::Polyhedron_3<Traits> (If it has only triangular faces), using the specialization boost::graph_traits< CGAL::Polyhedron_3<Traits> > .Related Functions | |
(Note that these are not member functions.) | |
| template<class EdgeCollapsableSurfaceMeshWithConstraints , class EdgeIsConstrainedMap > | |
| boost::graph_traits < EdgeCollapsableSurfaceMeshWithConstraints > ::vertex_descriptor | halfedge_collapse (typename boost::graph_traits< EdgeCollapsableSurfaceMeshWithConstraints >::edge_descriptor const &ue, EdgeCollapsableSurfaceMeshWithConstraints &surface_mesh, EdgeIsConstrainedMap edge_is_constrained_map) |
Collapses the undirected edge (v0v1,v1v0) replacing it with v0 or v1, as described in the paragraph above and guarantees that a halfedge he, for which get(edge_is_constrained_map, he)==true, is not removed after the collapse. More... | |
|
related |
Collapses the undirected edge (v0v1,v1v0) replacing it with v0 or v1, as described in the paragraph above and guarantees that a halfedge he, for which get(edge_is_constrained_map, he)==true, is not removed after the collapse.
| EdgeCollapsableSurfaceMeshWithConstraints | a model of HalfedgeGraph |
| EdgeIsConstrainedMap | a model of ReadablePropertyMap with the edge descriptor of EdgeCollapsableSurfaceMeshWithConstraints as key type and a boolean as value type. It indicates if an edge is constrained or not. |
surface_mesh to be an oriented 2-manifold with or without boundaries. Furthermore, the undirected edge (v0v1,v1v0) must satisfy the link condition [1], which guarantees that the surface mesh is also 2-manifold after the edge collapse. get(edge_is_constrained_map, v0v1)==get(edge_is_constrained_map, v1v0)==false. v0 and v1 are not both incident to a constrained edge.