|
CGAL 4.9 - 2D Apollonius Graphs (Delaunay Graphs of Disks)
|
|
CGAL 4.9 - 2D Apollonius Graphs (Delaunay Graphs of Disks)
|
The concept ApolloniusGraphDataStructure_2 refines the concept TriangulationDataStructure_2. In addition it provides two methods for the insertion and removal of a degree 2 vertex in the data structure. The insertion method adds a new vertex to the specified edge, thus creating two new edges. Moreover, it creates two new faces that have the two newly created edges in common (see figure below). The removal method performs the reverse operation.
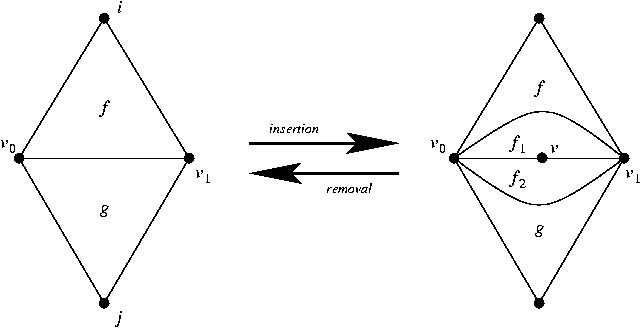
(f,i) is replaced by two edges by means of inserting a vertex v on the edge. The faces \( f_1\) and \( f_2\) are created. Right to left: the faces \( f_1\) and \( f_2\) are destroyed. The vertex v is deleted and its two adjacent edges are merged. We only describe the additional requirements with respect to the TriangulationDataStructure_2 concept.
Insertion | |
| Vertex_handle | insert_degree_2 (Face_handle f, int i) |
| Inserts a degree two vertex and two faces adjacent to it that have two common edges. More... | |
Removal | |
| void | remove_degree_2 (Vertex_handle v) |
| Removes a degree 2 vertex and the two faces adjacent to it. More... | |
| Vertex_handle ApolloniusGraphDataStructure_2::insert_degree_2 | ( | Face_handle | f, |
| int | i | ||
| ) |
Inserts a degree two vertex and two faces adjacent to it that have two common edges.
The edge defined by the face handle f and the integer i is duplicated. It returns a handle to the vertex created.
| void ApolloniusGraphDataStructure_2::remove_degree_2 | ( | Vertex_handle | v) |
Removes a degree 2 vertex and the two faces adjacent to it.
The two edges of the star of v that are not incident to it are collapsed.
v must be equal to 2.