|
CGAL 5.0.3 - Polynomial
|
|
CGAL 5.0.3 - Polynomial
|
Computes the polynomial subresultant of two polynomials \( p\) and \( q\) of type PolynomialTraits_d::Polynomial_d with respect to outermost variable. Let \( p=\ccSum{i=0,\ldots,n}{} p_i x^i\) and \( q=\ccSum{i=0,\ldots,m}{} q_i x^i\), where \( x\) is the outermost variable. The \( i\)-th subresultant (with \( i=0,\ldots,\min\{n,m\}\)) is defined by.
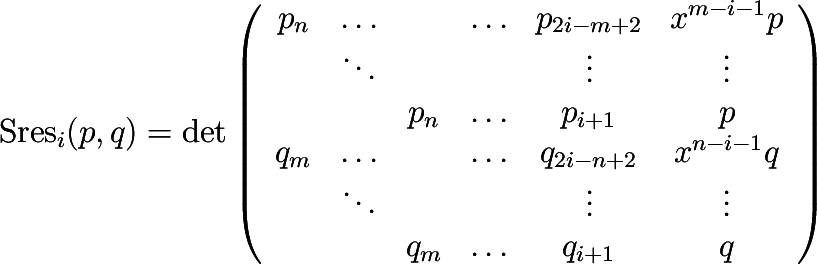
where \( p_i\) and \( q_i\) are set to zero if \( i<0\). In the case that \( n=m\), \( \mathrm{Sres_n}\) is set to \( q\).
The result is written in an output range, starting with the \( 0\)-th subresultant \( \mathrm{Sres}_0(p,q)\) (aka as the resultant of \( p\) and \( q\)).
Operations | |
| template<typename OutputIterator > | |
| OutputIterator | operator() (Polynomial_d p, Polynomial_d q, OutputIterator out) |
| computes the polynomial subresultants of \( p\) and \( q\), with respect to the outermost variable. More... | |
| template<typename OutputIterator > | |
| OutputIterator | operator() (Polynomial_d p, Polynomial_d q, OutputIterator out, int i) |
| computes the polynomial subresultants of \( p\) and \( q\), with respect to the variable \( x_i\). | |
| OutputIterator PolynomialTraits_d::PolynomialSubresultants::operator() | ( | Polynomial_d | p, |
| Polynomial_d | q, | ||
| OutputIterator | out | ||
| ) |
computes the polynomial subresultants of \( p\) and \( q\), with respect to the outermost variable.
Each element is of type PolynomialTraits_d::Polynomial_d.