|
CGAL 5.1.4 - 2D Polyline Simplification
|
|
CGAL 5.1.4 - 2D Polyline Simplification
|
This package allows to simplify polylines with the guarantee that the topology of the polylines does not change. This can be done for a single polyline as well as for a set of polyline constraints in a constrained triangulation. The simplification can be controlled with cost and stop functions.
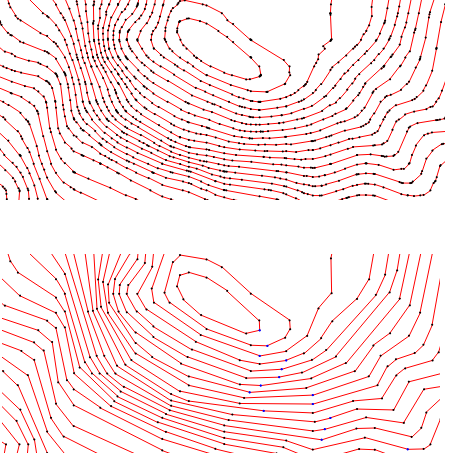
Polyline simplification is the process of reducing the number of vertices used in a set of polylines while keeping the overall shape as much as possible.
Topology preserving polyline simplification means that neither intersections are introduced, nor the nesting level of a polygon changes: islands do not intersect a simplified coastline, and islands stay in the water.
The method implemented in this package is based on [1]. It can simplify any set of polylines, open or closed, and possibly intersecting themselves or each other. The method consists of iteratively replacing edges (p,q) and (q,r) with edge (p,r) by removing the vertex q from one polyline. The topology of the polyline set is preserved during the simplification as the algorithm guarantees that no new intersections occur as a result of removing a vertex.
Vertices are removed according to a priority given for the vertex by a user-supplied cost function which calculates the simplification error. The cost function is a measure of the deviation between the original polyline and the current polyline without the vertex.
The algorithm terminates when a user-supplied stop predicate returns true, for instance, upon reaching a desired number of vertices or reaching a maximum simplification error.
The polyline simplification algorithm operates on a triangulation class from Chapter 2D Triangulation, namely Constrained_triangulation_plus_2. This data structure allows to remove vertices of a polyline constraint, while keeping the points of the removed vertices of the polyline constraint. The fact that it is a triangulation allows to perform the topology check for vertices p,q,r efficiently, as this can be decided based on the set of vertices adjacent to q in the triangulation.
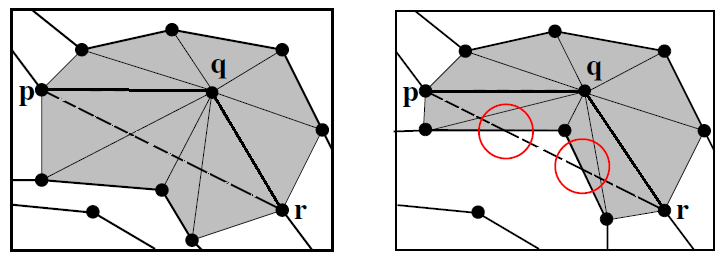
q can be removed. The specific way in which the removal cost is calculated is called the cost function. The user can choose different strategies by choosing a cost function object.
This package provides the three cost functions formulated in [1]. As the cost function is a template argument of the simplification function, users can write and use their own. The provided cost functions are all based on measuring the Euclidean distance between a subsequence of the original polyline and the corresponding subsequence of the simplified polyline with the vertex whose cost is calculated being removed.
Let vertices p, q, and r be three consecutive vertices of a polyline constraint. If the vertex q is removed, the edges (p,q) and (q,r) would be replaced by the edge (p,r).
The maximum squared distance is the maximum of the squared Euclidean distances between each point on the original polyline between p and r and the line segment (p,r). Let \(s_0,...,s_n\) be the points strictly between p and r on the original polyline. The cost of removing vertex q is: \( v_1 = \max \{ \mathrm{squared\_distance}((p,r), s_i) | i=0,..,n\} \)
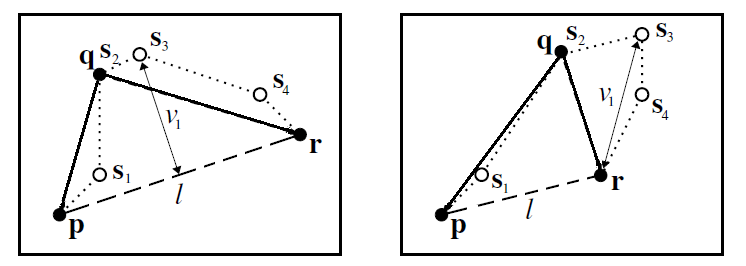
When it is important to preserve the separation of adjacent polylines, a variation of the maximum squared distance cost can be used. Here the maximum is divided by the minimum squared Euclidean distance between the candidate vertex q and all its adjacent vertices (except p and r). Those are all vertices in adjacent polylines, or adjacent regions of the same polyline.
Let \(t_0,...,t_m\) be the points of the vertices adjacent to vertex q, different from p and r and let \( v_2 = \min \{ \mathrm{squared\_distance}((p,r), t_i) | i=0,..,n\}\). The cost of removing vertex q is \(v_1/v_2\), and it is +infinity when the set of points \({t_1..t_m}\) is empty (possible if the point q is on the convex hull). See also Figure 22.3.
This distance measure gives lower priority to vertices with close neighboring polylines.
The scaled maximum works well in areas with close neighboring polylines, while the absolute maximum works better in areas where the polylines are far apart. In certain applications such as cartographic contours, there are both dense and spare areas, so a good strategy is to use a scaled or an absolute maximum depending on the case.
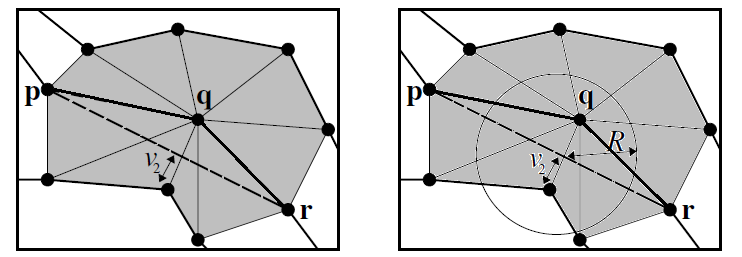
The hybrid distance measure uses a parameter \(R\) to indicate which measure to use: if \(v_2\) , i.e., the minimum distance to adjacent vertices, is below \(R\), the scaled maximum is used, otherwise the absolute maximum is used.
The cost of removing vertex q is \(v_1/v_2\), if \(v_2 <R\), and \(v_1/R\), otherwise.
As Dyken&al. explain, the choice of a good value for \(R\) is problem specific. It may depend on the pen size or the pixel size when drawing, or on the grid size when the polyline points are on a grid.
The first example shows how to simplify a Polygon_2. We then show how to simplify simultaneously several polylines, and show how to mark polyline vertices so that they do not get removed. The last example shows how to keep, access, and really remove points of polyline vertices that got removed by the simplification.
The first example shows how to simplify a single polyline by halving the number of vertices.
File Polyline_simplification_2/simplify_polygon.cpp
In the second example we insert several polygons in a Constrained_triangulation_plus_2. As a vertex type we have to use CGAL::Polyline_simplification_2::Vertex_base_2 as vertices may be marked as non-removable. The simplification algorithm marks the first and last vertex of polyline constraints as well as intersections. Finally, we iterate over all vertices of all polyline constraints.
File Polyline_simplification_2/simplify.cpp
In this example we show the version of Polyline_simplification_2::simplify() that simplifies a single polyline constraint, and keeps the points while removing vertices.
During the simplification the cost functions need the original sequence of points. As explained in the introduction the Constrained_triangulation_plus_2 allows to remove vertices from a polyline constraint, and hence from the triangulation, while keeping the points in the polyline constraint. This explains why there is a Vertices_in_constraint_iterator and a Point_in_constraint_iterator.
With the last argument of Polyline_simplification_2::simplify() set to true, we can keep the points even when the simplification function has returned. We might want to keep them, because we want to call Polyline_simplification_2::simplify() once again for the same polyline constraint, while measuring the simplification error against the original polyline.
The print function traverses each polyline constraint twice. First we print the points on the simplified polyline, and then we print the points of the original polyline.
At the end we remove the points that were kept from the constraints.
File Polyline_simplification_2/points_and_vertices.cpp
It is possible to use the class Projection_traits_xy_3 in order to simplify polylines in space. Note that the segment length is computed in the xy-plane, and the polyline must not have any vertical segment.
File Polyline_simplification_2/simplify_terrain.cpp
Dyken et al [1] combine a classical polyline simplification algorithm with the triangulation of polylines in order to check if an elementary simplification step can be performed. In our implementation we simplified this test even further.
Fernando Cacciola made a first prototype implementation for GeometryFactory.