User Manual

Author

Xiang Gao, Sébastien Loriot and Andrea Tagliasacchi

Introduction

Figure 72.1 Curve skeleton of a horse model.

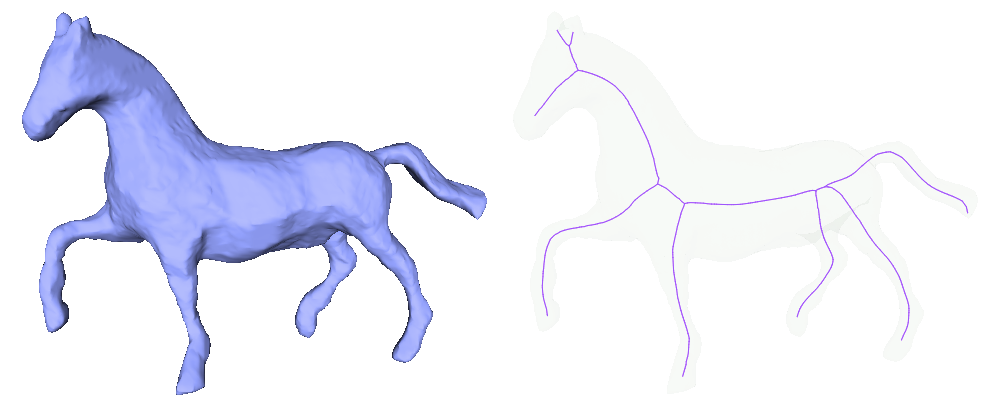
Skeletons are effective shape abstractions used in segmentation, shape matching, reconstruction, virtual navigation, etc. As the name implies, a curve skeleton is a graph of curvilinear structures (1D). It is not a medial axis that for a 3D geometry is composed of surfaces (2D). As illustrated in Figure 72.1, the curve skeleton of a shape captures its essential topology. In this package, we implement the Mean Curvature Skeleton algorithm described in [1] that extracts a curve skeleton from a triangulated surface mesh without borders by iteratively contracting the input triangulated surface mesh.

User Interface Description

Input and Output

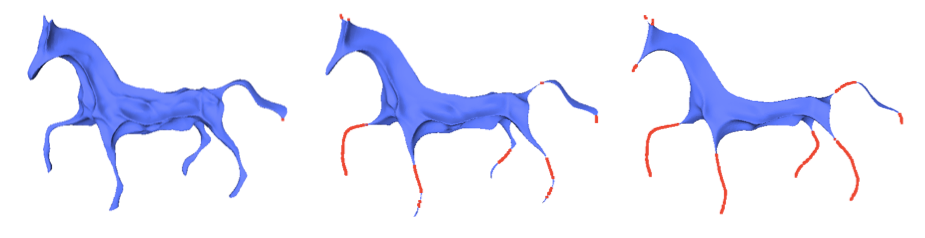
The input is a triangulated surface mesh, model of the FaceListGraph concept (CGAL::Surface_mesh, CGAL::Polyhedron_3, ...) that has no boundary and that has only one connected component. The skeleton is provided as a graph of type boost::adjacency_list. Each vertex of the skeleton is associated to a 3D location point and to the set of input vertices that contracted to that skeleton vertex. Note that due to the construction process of the skeleton, a skeleton vertex might have no corresponding input vertex.

This package needs a sparse linear solver and we recommend the use of Eigen 3.2 or later.

The input and output are illustrated in Figure 72.2.

Figure 72.2 Left: An input triangulated surface mesh model of an octopus; Middle: The mean curvature flow skeleton extracted using this package; Right: Each vertex of the input surface is associated to a skeleton vertex.

Free Function

If a CGAL model of the FaceListGraph concept such as CGAL::Surface_mesh or CGAL::Polyhedron_3 is used as triangulated input surface mesh, Eigen 3.2 or later is available and CGAL_EIGEN3_ENABLED is defined, the function CGAL::extract_mean_curvature_flow_skeleton() can be used to extract a mean curvature flow skeleton from the input surface mesh using the default parameters, which work well in most cases.

The following example shows how to extract a skeleton out of a triangulated surface mesh and how to access the point of each skeleton vertex and the set of input vertices associated.

File Surface_mesh_skeletonization/simple_mcfskel_example.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/extract_mean_curvature_flow_skeleton.h>
#include <CGAL/boost/graph/split_graph_into_polylines.h>
#include <fstream>


typedef CGAL::Simple_cartesian<double>                        Kernel;
typedef Kernel::Point_3                                       Point;
typedef CGAL::Polyhedron_3<Kernel>                            Polyhedron;

typedef boost::graph_traits<Polyhedron>::vertex_descriptor    vertex_descriptor;

typedef CGAL::Mean_curvature_flow_skeletonization<Polyhedron> Skeletonization;
typedef Skeletonization::Skeleton                             Skeleton;

typedef Skeleton::vertex_descriptor                           Skeleton_vertex;
typedef Skeleton::edge_descriptor                             Skeleton_edge;

//only needed for the display of the skeleton as maximal polylines
struct Display_polylines{
  const Skeleton& skeleton;
  std::ofstream& out;
  int polyline_size;
  std::stringstream sstr;

  Display_polylines(const Skeleton& skeleton, std::ofstream& out)
    : skeleton(skeleton), out(out)
  {}

  void start_new_polyline(){
    polyline_size=0;
    sstr.str("");
    sstr.clear();
  }
  void add_node(Skeleton_vertex v){
    ++polyline_size;
    sstr << " " << skeleton[v].point;
  }
  void end_polyline()
  {
    out << polyline_size << sstr.str() << "\n";
  }
};

// This example extracts a medially centered skeleton from a given mesh.
int main(int argc, char* argv[])
{
  std::ifstream input((argc>1)?argv[1]:"data/elephant.off");
  Polyhedron tmesh;
  input >> tmesh;
  if (!CGAL::is_triangle_mesh(tmesh))
  {
    std::cout << "Input geometry is not triangulated." << std::endl;
    return EXIT_FAILURE;
  }

  Skeleton skeleton;

  CGAL::extract_mean_curvature_flow_skeleton(tmesh, skeleton);

  std::cout << "Number of vertices of the skeleton: " << boost::num_vertices(skeleton) << "\n";
  std::cout << "Number of edges of the skeleton: " << boost::num_edges(skeleton) << "\n";

  // Output all the edges of the skeleton.
  std::ofstream output("skel-poly.cgal");
  Display_polylines display(skeleton,output);
  CGAL::split_graph_into_polylines(skeleton, display);
  output.close();

  // Output skeleton points and the corresponding surface points
  output.open("correspondance-poly.cgal");
  for(Skeleton_vertex v : CGAL::make_range(vertices(skeleton)))
    for(vertex_descriptor vd : skeleton[v].vertices)
      output << "2 " << skeleton[v].point << " "
                     << get(CGAL::vertex_point, tmesh, vd)  << "\n";

  return EXIT_SUCCESS;
}

Advanced Usage with the Function Object

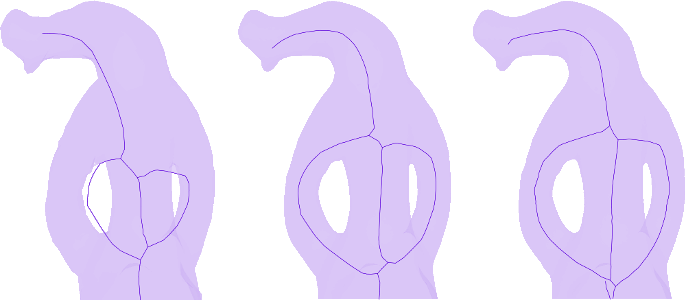
The class CGAL::Mean_curvature_flow_skeletonization enables the usage of low level functions such as contract_geometry() and collapse_edges(). The class further enables to change the parameters of the algorithm, for example by calling set_is_medially_centered(). The class gives the user full control over each step of the algorithm as well as the intermediate contracted mesh (called meso-skeleton) as illustrated by Figure 72.3.

Figure 72.3 Three iterations of the mean curvature flow contraction of the horse of Figure 72.1. The red points indicate vertices where the surface has locally degenerated to a curvilinear structure.

In this example, we show how to use the API of the class CGAL::Mean_curvature_flow_skeletonization.

File Surface_mesh_skeletonization/MCF_Skeleton_sm_example.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Mean_curvature_flow_skeletonization.h>

#include <fstream>

typedef CGAL::Simple_cartesian<double>                        Kernel;
typedef Kernel::Point_3                                       Point;
typedef CGAL::Surface_mesh<Point>                             Triangle_mesh;

typedef boost::graph_traits<Triangle_mesh>::vertex_descriptor vertex_descriptor;

typedef CGAL::Mean_curvature_flow_skeletonization<Triangle_mesh> Skeletonization;
typedef Skeletonization::Skeleton                             Skeleton;

typedef Skeleton::vertex_descriptor                           Skeleton_vertex;
typedef Skeleton::edge_descriptor                             Skeleton_edge;

int main(int argc, char* argv[])
{
  std::ifstream input((argc>1)?argv[1]:"data/elephant.off");
  Triangle_mesh tmesh;
  input >> tmesh;
  if (!CGAL::is_triangle_mesh(tmesh))
  {
    std::cout << "Input geometry is not triangulated." << std::endl;
    return EXIT_FAILURE;
  }

  Skeleton skeleton;
  Skeletonization mcs(tmesh);

  // 1. Contract the mesh by mean curvature flow.
  mcs.contract_geometry();

  // 2. Collapse short edges and split bad triangles.
  mcs.collapse_edges();
  mcs.split_faces();

  // 3. Fix degenerate vertices.
  mcs.detect_degeneracies();

  // Perform the above three steps in one iteration.
  mcs.contract();

  // Iteratively apply step 1 to 3 until convergence.
  mcs.contract_until_convergence();

  // Convert the contracted mesh into a curve skeleton and
  // get the correspondent surface points
  mcs.convert_to_skeleton(skeleton);

  std::cout << "Number of vertices of the skeleton: " << boost::num_vertices(skeleton) << "\n";
  std::cout << "Number of edges of the skeleton: " << boost::num_edges(skeleton) << "\n";

  // Output all the edges of the skeleton.
  std::ofstream output("skel-sm.cgal");
  for(Skeleton_edge e : CGAL::make_range(edges(skeleton)))
  {
    const Point& s = skeleton[source(e, skeleton)].point;
    const Point& t = skeleton[target(e, skeleton)].point;
    output << "2 "<< s << " " << t << "\n";
  }
  output.close();

  // Output skeleton points and the corresponding surface points
  output.open("correspondance-sm.cgal");
  for(Skeleton_vertex v : CGAL::make_range(vertices(skeleton)))
    for(vertex_descriptor vd : skeleton[v].vertices)
      output << "2 " << skeleton[v].point << "  " << get(CGAL::vertex_point, tmesh, vd)  << "\n";

  return EXIT_SUCCESS;
}

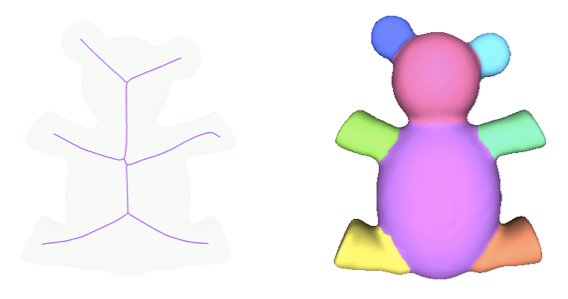
Segmentation through Skeletonization

As a proof of concept, we show how to use the skeleton and the association of input vertices to skeleton to compute a segmentation of the input triangulated surface mesh using the package Triangulated Surface Mesh Segmentation. The segmentation algorithm consists in computing a shape diameter function for each face of the input mesh, followed by solving a graph cut problem. Here we use the skeleton to define a new shape diameter function. Specifically, for each face we compute the diameter value as the average distance between its three incident vertices and their corresponding skeletal point. The result of this segmentation is shown in Figure 72.4.

Figure 72.4 Left: Curve skeleton extracted of a triangulated surface mesh; Right: Segmentation using the skeleton to compute a shape diameter function.

File Surface_mesh_skeletonization/segmentation_example.cpp

#include <CGAL/Polyhedron_3.h>
#include <CGAL/Polyhedron_items_with_id_3.h>
#include <CGAL/Simple_cartesian.h>
#include <CGAL/extract_mean_curvature_flow_skeleton.h>
#include <CGAL/mesh_segmentation.h>

#include <fstream>

typedef CGAL::Simple_cartesian<double>                               Kernel;
typedef Kernel::Point_3                                              Point;
typedef CGAL::Polyhedron_3<Kernel, CGAL::Polyhedron_items_with_id_3> Polyhedron;

typedef boost::graph_traits<Polyhedron>::vertex_descriptor           vertex_descriptor;
typedef boost::graph_traits<Polyhedron>::halfedge_descriptor         halfedge_descriptor;
typedef boost::graph_traits<Polyhedron>::face_descriptor             face_descriptor;

typedef CGAL::Mean_curvature_flow_skeletonization<Polyhedron>        Skeletonization;
typedef Skeletonization::Skeleton                                    Skeleton;

typedef Skeleton::vertex_descriptor                                  Skeleton_vertex;

// Property map associating a facet with an integer as id to an
// element in a vector stored internally
template<class ValueType>
struct Facet_with_id_pmap
    : public boost::put_get_helper<ValueType&,
             Facet_with_id_pmap<ValueType> >
{
    typedef face_descriptor key_type;
    typedef ValueType value_type;
    typedef value_type& reference;
    typedef boost::lvalue_property_map_tag category;

    Facet_with_id_pmap(
      std::vector<ValueType>& internal_vector
    ) : internal_vector(internal_vector) { }

    reference operator[](key_type key) const
    { return internal_vector[key->id()]; }
private:
    std::vector<ValueType>& internal_vector;
};


int main(int argc, char* argv[])
{
  std::ifstream input((argc>1)?argv[1]:"data/161.off");
  Polyhedron tmesh;
  input >> tmesh;
  if (!CGAL::is_triangle_mesh(tmesh))
  {
    std::cout << "Input geometry is not triangulated." << std::endl;
    return EXIT_FAILURE;
  }

  // extract the skeleton
  Skeleton skeleton;
  CGAL::extract_mean_curvature_flow_skeleton(tmesh, skeleton);

  // init the polyhedron simplex indices
  CGAL::set_halfedgeds_items_id(tmesh);

  //for each input vertex compute its distance to the skeleton
  std::vector<double> distances(num_vertices(tmesh));
  for(Skeleton_vertex v : CGAL::make_range(vertices(skeleton)) )
  {
    const Point& skel_pt = skeleton[v].point;
    for(vertex_descriptor mesh_v : skeleton[v].vertices)
    {
      const Point& mesh_pt = mesh_v->point();
      distances[mesh_v->id()] = std::sqrt(CGAL::squared_distance(skel_pt, mesh_pt));
    }
  }

  // create a property-map for sdf values
  std::vector<double> sdf_values( num_faces(tmesh) );
  Facet_with_id_pmap<double> sdf_property_map(sdf_values);

  // compute sdf values with skeleton
  for(face_descriptor f : faces(tmesh))
  {
    double dist = 0;
    for(halfedge_descriptor hd : halfedges_around_face(halfedge(f, tmesh), tmesh))
      dist+=distances[target(hd, tmesh)->id()];
    sdf_property_map[f] = dist / 3.;
  }

  // post-process the sdf values
  CGAL::sdf_values_postprocessing(tmesh, sdf_property_map);

  // create a property-map for segment-ids (it is an adaptor for this case)
  std::vector<std::size_t> segment_ids( num_faces(tmesh) );
  Facet_with_id_pmap<std::size_t> segment_property_map(segment_ids);

  // segment the mesh using default parameters
  std::cout << "Number of segments: "
            << CGAL::segmentation_from_sdf_values(tmesh, sdf_property_map, segment_property_map) <<"\n";

  return EXIT_SUCCESS;
}

Performance

The elephant model is used to illustrate the performance of the mean curvature flow skeletonization procedure. Different resolutions of the model obtained by loop subdivision are used.

As can be seen on Figure 72.5, the more sampled the surface is, the better the skeleton is inside the model.

Figure 72.5 Skeleton of the head of the elephant model. Left: Using the original mesh (2,775 vertices); Middle: After one loop subdivision step (11,112 vertices); Right: After two loops subdivision steps (44,460 vertices).

Runtime in milliseconds of extract_mean_curvature_flow_skeleton() using Polyhedron_3<Simple_cartesian<double> > as input data structure. The runtimes are similar if Surface_mesh<Simple_cartesian<double>::Point_3> is used instead. The solver used is the default one when Eigen is available. The code was compiled using CGAL 4.7 with g++ 4.8.4 with -O3 -DNDEBUG as compiling flags and was run on a Intel(R) Core(TM) i7-2820QM CPU @ 2.30GHz

Number of loop subdivision of elephant.off	Number of vertices	Runtime in s
0	2,775	0.46
1	11,112	1.26
2	44,460	5.64
3	177,852	26.26

Design and Implementation History

The initial implementation of this package is the result of the work of Xiang Gao during the 2013 season of the Google Summer of Code mentored by Andrea Tagliasacchi and Sébastien Loriot. It was finalized by Andreas Fabri and Sébastien Loriot.