|
CGAL 5.3.1 - Algebraic Foundations
|
|
CGAL 5.3.1 - Algebraic Foundations
|
CGAL is targeting towards exact computation with non-linear objects, in particular objects defined on algebraic curves and surfaces. As a consequence types representing polynomials, algebraic extensions and finite fields play a more important role in related implementations. This package has been introduced to stay abreast of these changes. Since in particular polynomials must be supported by the introduced framework the package avoids the term number type. Instead the package distinguishes between the algebraic structure of a type and whether a type is embeddable on the real axis, or real embeddable for short. Moreover, the package introduces the notion of interoperable types which allows an explicit handling of mixed operations.
The algebraic structure concepts introduced within this section are motivated by their well known counterparts in traditional algebra, but we also had to pay tribute to existing types and their restrictions. To keep the interface minimal, it was not desirable to cover all known algebraic structures, e.g., we did not introduce concepts for such basic structures as groups or exceptional structures as skew fields.
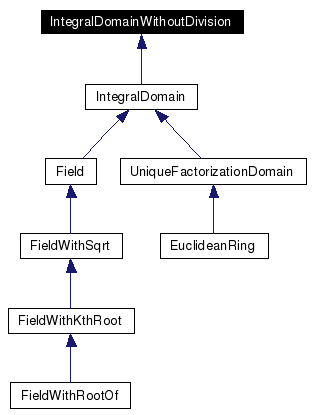
Figure 1.1 shows the refinement relationship of the algebraic structure concepts. IntegralDomain, UniqueFactorizationDomain, EuclideanRing and Field correspond to the algebraic structures with the same name. FieldWithSqrt, FieldWithKthRoot and FieldWithRootOf are fields that in addition are closed under the operations 'sqrt', 'k-th root' and 'real root of a polynomial', respectively. The concept IntegralDomainWithoutDivision also corresponds to integral domains in the algebraic sense, the distinction results from the fact that some implementations of integral domains lack the (algebraically always well defined) integral division. Note that Field refines IntegralDomain. This is because most ring-theoretic notions like greatest common divisors become trivial for Fields. Hence we see Field as a refinement of IntegralDomain and not as a refinement of one of the more advanced ring concepts. If an algorithm wants to rely on gcd or remainder computation, it is trying to do things it should not do with a Field in the first place.
The main properties of an algebraic structure are collected in the class Algebraic_structure_traits. In particular the (most refined) concept each concrete model AS fulfills is encoded in the tag Algebraic_structure_traits<AS>::Algebraic_category . An algebraic structure is at least Assignable, CopyConstructible, DefaultConstructible and EqualityComparable. Moreover, we require that it is constructible from int. For ease of use and since their semantic is sufficiently standard to presume their existence, the usual arithmetic and comparison operators are required to be realized via C++ operator overloading. The division operator is reserved for division in fields. All other unary (e.g., sqrt) and binary functions (e.g., gcd, div) must be models of the well known STL-concepts AdaptableUnaryFunction or AdaptableBinaryFunction concept and local to the traits class (e.g., Algebraic_structure_traits<AS>::Sqrt()(x) ). This design allows us to profit from all parts in the STL and its programming style and avoids the name-lookup and two-pass template compilation problems experienced with the old design using overloaded functions. However, for ease of use and backward compatibility all functionality is also accessible through global functions defined within namespace CGAL, e.g., CGAL::sqrt(x) . This is realized via function templates using the according functor of the traits class. For an overview see Section Algebraic Foundations Reference in the reference manual.
For a type AS, Algebraic_structure_traits<AS> provides several tags. The most important tag is the Algebraic_category tag, which indicates the most refined algebraic concept the type AS fulfills. The tag is one of; Integral_domain_without_division_tag, Integral_domain_tag, Field_tag, Field_with_sqrt_tag, Field_with_kth_root_tag, Field_with_root_of_tag, Unique_factorization_domain_tag, Euclidean_ring_tag, or even Null_tag in case the type is not a model of an algebraic structure concept. The tags are derived from each other such that they reflect the hierarchy of the algebraic structure concept, e.g., Field_with_sqrt_tag is derived from Field_tag.
Moreover, Algebraic_structure_traits<AS> provides the tags Is_exact and Is_numerical_sensitive, which are both Boolean_tags.
An algebraic structure is considered exact, if all operations required by its concept are computed such that a comparison of two algebraic expressions is always correct.
An algebraic structure is considered as numerically sensitive, if the performance of the type is sensitive to the condition number of an algorithm. Note that there is really a difference among these two notions, e.g., the fundamental type int is not numerical sensitive but considered inexact due to overflow. Conversely, types as leda_real or CORE::Expr are exact but sensitive to numerical issues due to the internal use of multi precision floating point arithmetic. We expect that Is_numerical_sensitive is used for dispatching of algorithms, while Is_exact is useful to enable assertions that can be check for exact types only.
Tags are very useful to dispatch between alternative implementations. The following example illustrates a dispatch for Fields using overloaded functions. The example only needs two overloads since the algebraic category tags reflect the algebraic structure hierarchy.
File Algebraic_foundations/algebraic_structure_dispatch.cpp
Most number types represent some subset of the real numbers. From those types we expect functionality to compute the sign, absolute value or double approximations. In particular we can expect an order on such a type that reflects the order along the real axis. All these properties are gathered in the concept RealEmbeddable. The concept is orthogonal to the algebraic structure concepts, i.e., it is possible that a type is a model of RealEmbeddable only, since the type may just represent values on the real axis but does not provide any arithmetic operations.
As for algebraic structures this concept is also traits class oriented. The main functionality related to RealEmbeddable is gathered in the class Real_embeddable_traits. In particular, it provides the boolean tag Is_real_embeddable indicating whether a type is a model of RealEmbeddable. The comparison operators are required to be realized via C++ operator overloading. All unary functions (e.g. sign, to_double) and binary functions (e.g. compare ) are models of the STL-concepts AdaptableUnaryFunction and AdaptableBinaryFunction and are local to Real_embeddable_traits.
In case a type is a model of IntegralDomainWithoutDivision and RealEmbeddable the number represented by an object of this type is the same for arithmetic and comparison. It follows that the ring represented by this type is a superset of the integers and a subset of the real numbers and hence has characteristic zero.
In case the type is a model of Field and RealEmbeddable it is a superset of the rational numbers.
Every CGAL Kernel comes with two real number types (number types embeddable into the real numbers). One of them is a FieldNumberType, and the other a RingNumberType. The coordinates of the basic kernel objects (points, vectors, etc.) come from one of these types (the FieldNumberType in case of Cartesian kernels, and the RingNumberType for Homogeneous kernels).
The concept FieldNumberType combines the requirements of the concepts Field and RealEmbeddable, while RingNumberType combines IntegralDomainWithoutDivision and RealEmbeddable. Algebraically, the real number types do not form distinct structures and are therefore not listed in the concept hierarchy of Figure 1.1.
This section introduces two concepts for interoperability of types, namely ImplicitInteroperable and ExplicitInteroperable. While ExplicitInteroperable is the base concept, we start with ImplicitInteroperable since it is the more intuitive one.
In general mixed operations are provided by overloaded operators and functions or just via implicit constructor calls. This level of interoperability is reflected by the concept ImplicitInteroperable. However, within template code the result type, or so called coercion type, of a mixed arithmetic operation may be unclear. Therefore, the package introduces Coercion_traits giving access to the coercion type via Coercion_traits<A,B>::Type for two interoperable types A and B.
Some trivial example are int and double with coercion type double or Gmpz and Gmpq with coercion type Gmpq. However, the coercion type is not necessarily one of the input types, e.g. the coercion type of a polynomial with integer coefficients that is multiplied by a rational type is supposed to be a polynomial with rational coefficients.
Coercion_traits is also required to provide a functor Coercion_traits<A,B>::Cast() , that converts from an input type into the coercion type. This is in fact the core of the more basic concept ExplicitInteroperable. ExplicitInteroperable has been introduced to cover more complex cases for which it is hard or impossible to guarantee implicit interoperability. Note that this functor can be useful for ImplicitInteroperable types as well, since it can be used to void redundant type conversions.
In case two types A and B are ExplicitInteroperable with coercion type C they are valid argument types for all binary functors provided by Algebraic_structure_traits and Real_embeddable_traits of C. This is also true for the according global functions.
The following example illustrates how two write code for ExplicitInteroperable types.
File Algebraic_foundations/interoperable.cpp
The following example illustrates a dispatch for ImplicitInteroperable and ExplicitInteroperable types. The binary function (that just multiplies its two arguments) is supposed to take two ExplicitInteroperable arguments. For ImplicitInteroperable types a variant that avoids the explicit cast is selected.
File Algebraic_foundations/implicit_interoperable_dispatch.cpp
Beyond the need for performing algebraic operations on objects as a whole, there are also number types which one would like to decompose into numerator and denominator. This does not only hold for rational numbers as Quotient, Gmpq, mpq_class or leda_rational, but also for compound objects as Sqrt_extension or Polynomial which may decompose into a (scalar) denominator and a compound numerator with a simpler coefficient type (e.g. integer instead of rational). Often operations can be performed faster on these denominator-free multiples. In case a type is a Fraction the relevant functionality as well as the numerator and denominator type are provided by Fraction_traits. In particular Fraction_traits provides a tag Is_fraction that can be used for dispatching.
A related class is Rational_traits which has been kept for backward compatibility reasons. However, we recommend to use Fraction_traits since it is more general and offers dispatching functionality.
The following example show a simple use of Fraction_traits:
File Algebraic_foundations/fraction_traits.cpp
The following example illustrates the integralization of a vector, i.e., the coefficient vector of a polynomial. Note that for minimizing coefficient growth Fraction_traits<Type>::Common_factor is used to compute the least common multiple of the denominators.
File Algebraic_foundations/integralize.cpp
The package is part of CGAL since release 3.3. Of course the package is based on the former Number type support of CGAL. This goes back to Stefan Schirra and Andreas Fabri. But on the other hand the package is to a large extend influenced by the experience with the number type support in Exacus [1], which in the main goes back to Lutz Kettner, Susan Hert, Arno Eigenwillig and Michael Hemmer. However, the package abstracts from the pure support for number types that are embedded on the real axis which allows the support of polynomials, finite fields, and algebraic extensions as well. See also related subsequent chapters.