|
CGAL 5.4 - Geometric Object Generators
|
|
CGAL 5.4 - Geometric Object Generators
|
A variety of generators for geometric objects are provided in CGAL. They are useful as synthetic test data sets, e.g. for testing algorithms on degenerate object sets and for performance analysis.
Two kinds of point generators are provided: first, random point generators and second deterministic point generators. Most random point generators and a few deterministic point generators are provided as input iterators. The input iterators model an infinite sequence of points. The function CGAL::copy_n() can be used to copy a finite sequence. The iterator adaptor Counting_iterator can be used to create finite iterator ranges. Other generators are provided as functions that write to output iterators. Further functions add degeneracies or random perturbations.
In 2D, we provide input iterators to generate random points in a disc (Random_points_in_disc_2), in a square (Random_points_in_square_2), on a circle (Random_points_on_circle_2), on a segment (Random_points_on_segment), in a square (Random_points_on_square_2), in a triangle (Random_points_in_triangle_2), in a range of triangles (Random_points_in_triangles_2), and in a triangle mesh (Random_points_in_triangle_mesh_2). For generating grid points we provide three functions, points_on_segment_2(), points_on_square_grid_2() that write to output iterators and an input iterator Points_on_segment_2.
For 3D points, input iterators are provided for random points uniformly distributed in a sphere (Random_points_in_sphere_3), in a triangle (Random_points_in_triangle_3), in a range of triangles (Random_points_in_triangles_3), in a tetrahedron (Random_points_in_tetrahedron_3), in a cube (Random_points_in_cube_3), on the boundary of a sphere (Random_points_on_sphere_3), in a triangle mesh (Random_points_in_triangle_mesh_3), in a tetrahedron mesh (Random_points_in_tetrahedral_mesh_3), and on the boundary of a tetrahedron mesh (Random_points_in_tetrahedral_mesh_boundary_3). For generating 3D grid points, we provide the function points_on_cube_grid_3() that writes to an output iterator.
For higher dimensions, input iterators are provided for random points uniformly distributed in a d-dimensional cube (Random_points_in_cube_d) or d-dimensional ball (Random_points_in_ball_d) or on the boundary of a sphere (Random_points_on_sphere_d). For generating grid points, we provide the function points_on_cube_grid_d() that writes to an output iterator.
We also provide two functions for generating more complex geometric objects. The function random_convex_set_2() computes a random convex planar point set of a given size where the points are drawn from a specific domain and random_polygon_2() generates a random simple polygon from points drawn from a specific domain. The function random_convex_hull_in_disc_2() computes a random polygon as a convex hull from uniformly generated random points in a disc.
Degenerate input sets like grid points can be randomly perturbed by a small amount to produce quasi-degenerate test sets. This challenges numerical stability of algorithms using inexact arithmetic and exact predicates to compute the sign of expressions slightly off from zero. For this the function perturb_points_2() is provided.
For a given point set certain kinds of degeneracies can be produced by adding new points. The random_selection() function is useful for generating multiple copies of identical points. The function random_collinear_points_2() adds collinearities to a point set.
The function random_selection() chooses n items at random from a random access iterator range which is useful to produce degenerate input data sets with multiple entries of identical items.
The class Combination_enumerator<CombinationElement> is used to enumerate all fixed-size combinations (subsets) of a range of elements. It is useful in the context of high-dimensional triangulations, e.g., for enumerating the faces of a simplex.
We want to generate a test set of 1000 points, where 60% are chosen randomly in a small disc, 20% are from a larger grid, 10% are duplicates points, and 10% collinear points. A random shuffle removes the construction order from the test set. See Figure 107.1 for the example output.
File Generator/random_degenerate_point_set.cpp

The second example demonstrates the point generators with integer points. Floating point arithmetic is sufficient to produce regular integer grids. See Figure 107.2 for the example output.
File Generator/random_grid.cpp

The following example demonstrates the use of the random point generator on a triangle mesh. We want to generate 100 points uniformly chosen on a Polyhedron_3. See Figure 107.3
File Generator/random_points_on_triangle_mesh_3.cpp
The following two examples illustrate the use of the generic functions from Section Generic Algorithms like Join_input_iterator_2 to generate composed objects from other generators - here two-dimensional segments from two point generators.
We want to generate a test set of 200 segments, where one endpoint is chosen randomly from a horizontal segment of length 200, and the other endpoint is chosen randomly from a circle of radius 250. See Figure 107.4 for the example output.
File Generator/random_segments1.cpp

The second example generates a regular structure of 100 segments; see Figure 107.5 for the example output. It uses the Points_on_segment_2 iterator, Join_input_iterator_2 and Counting_iterator to avoid any intermediate storage of the generated objects until they are used.
File Generator/random_segments2.cpp

The following example generates points inside a cube in dimension 5 (examples for ball and sphere are available in the example directory) :
File Generator/cube_d.cpp
The output of this example looks like:
Generating 10 random points in a cube in 5D, coordinates from -100 to 100 5 32.9521 26.0403 59.3979 -99.2553 15.5102 5 80.3731 30.809 7.32491 -90.2544 94.5635 5 -71.3412 -31.933 -98.0734 79.6493 66.6104 5 -78.5065 -58.2397 -33.9096 81.2196 57.2512 5 21.4093 26.7661 57.6083 23.4958 93.1047 5 10.5895 -21.8914 70.9726 36.756 -42.2667 5 23.9813 54.4519 -26.0894 -85.18 -21.0775 5 -48.7499 59.9873 6.22335 -4.16011 81.0727 5 -11.6615 5.53147 -32.6578 -79.9283 44.5679 5 53.0183 78.3228 -28.5665 83.3503 68.0482
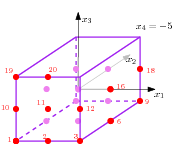
Next example generates grid points in dimension d=4. Since the required number of points, 20 is between \( 2^d\) and \( 3^d\) the supporting grid has \( 3\times 3\times 3\times 3\) points. Since the size parameter is 5, the coordinates are in \( \{-5, 0, 5\}\), but since the number of points verifies \( 20\leq 3^{d-1}\), all generated points have the same last coordinate \( -5\).
File Generator/grid_d.cpp
The output of previous example corresponds to the points of this figure depicted in red or pink (pink points are "inside" the cube). The output is:
Generating 20 grid points in 4D 4 -5 -5 -5 -5 4 0 -5 -5 -5 4 5 -5 -5 -5 4 -5 0 -5 -5 4 0 0 -5 -5 4 5 0 -5 -5 4 -5 5 -5 -5 4 0 5 -5 -5 4 5 5 -5 -5 4 -5 -5 0 -5 4 0 -5 0 -5 4 5 -5 0 -5 4 -5 0 0 -5 4 0 0 0 -5 4 5 0 0 -5 4 -5 5 0 -5 4 0 5 0 -5 4 5 5 0 -5 4 -5 -5 5 -5 4 0 -5 5 -5
The following example enumerates and outputs all subsets of 3 elements from the range \( [10, 15]\). Accordingly, it outputs \( \frac{6!}{3! 3!}=20\) triples.
File Generator/combination_enumerator.cpp
The output of this example is:
Taking 3 distinct integers in the range [10, 15]: {10 11 12} {10 11 13} {10 11 14}
{10 11 15} {10 12 13} {10 12 14} {10 12 15} {10 13 14} {10 13 15} {10 14 15}
{11 12 13} {11 12 14} {11 12 15} {11 13 14} {11 13 15} {11 14 15} {12 13 14}
{12 13 15} {12 14 15} {13 14 15}
Enumerated 20 combinations.
The following example generates all pairs of names from a set of names stored in an array of strings.
Lutz Kettner coded generators in 2D and 3D For points in and on sphere, points are generated in a cube up to the moment the point is inside the sphere, then it is normalized to go on the boundary if needed.
Sven Schönherr implemented the Random class.
Michael Hoffmann coded the random convex polygon,
Geert-Jan Giezeman and Susan Hert coded the random simple polygon.
Olivier Devillers coded generators in high dimensions. For points in ball and on sphere, points are generated on a sphere/ball boundary as a product of normal distributions, then it is normalized. If needed a random radius (with relevant distribution) is used to put the point inside the ball.
Remy Thomasse coded the random convex hull in a disc.
During Google Summer of Code 2013, Pedro M. M. de Castro and Alexandru Tifrea coded generators for points in triangle (2D and 3D) and in tetrahedra (3D). Basically, in order to generate a random point in a \(N\)-simplex (a triangle for \(N = 2\), and tetrahedron for \(N = 3\)), we generate numbers \(a_1,a_2,\ldots,a_N\) identically and independently uniformly distributed in \((0,1)\), we sort them, we let \(a_0 = 0\) and \(a_{N+1} = 1\), and then \(a_{i+1}-a_i\), for \(i = 1,\ldots,N\) becomes its barycentric coordinates with respect to the simplex.
Maxime Gimemo introduced the random generators on 2D and 3D triangle meshes.