|
CGAL 5.4.2 - dD Triangulations
|
|
CGAL 5.4.2 - dD Triangulations
|
This package proposes data structures and algorithms to compute triangulations of points in any dimensions [1]. The Triangulation_data_structure handles the combinatorial aspect of triangulations while the geometric classes Triangulation, Delaunay_triangulation and Regular_triangulation allow to compute and maintain triangulations, Delaunay triangulations, and regular triangulations of sets of points.
A finite abstract simplicial complex is built on a finite set of vertices \( V\) and consists of a collection \( S\) of subsets of \( V\) such that, if \( s\) is a set of vertices in \( S\), then all the subsets of \( s\) are also in \( S\).
The sets in \( S\) (which are subsets of \( V\)) are called faces or simplices (the singular of which is simplex). A simplex \( s\in S\) is maximal if it is not a proper subset of some other set in \( S\). A simplex having \( k+1 \) vertices is said of dimension \( k \). An \( k\)-face denotes a \( k\)-dimensional simplex, i.e., a simplex with \( k+1\) vertices. The simplicial complex is pure if all the maximal simplices have the same dimension.
A triangulation is a simplicial complex that is pure, connected and without boundaries nor singularities. The dimension of the triangulation is the dimension of its maximal simplices.
In the sequel, we will call these maximal simplices full cells. A face of a simplex is a subset of this simplex. A proper face of a simplex is a strict subset of this simplex. Two faces \( \sigma\) and \( \sigma'\) are incident if and only if \( \sigma'\) is a proper face of \( \sigma\) or vice versa.
A complex has no boundaries if any proper face of a simplex is also a proper face of another simplex.
If the triangulation is of dimension \( d \), we use the following terminology:
If the vertices are embedded into Euclidean space \( \mathbb{R}^n\), we deal with finite simplicial complexes, which have slightly different simplices and additional requirements:
This CGAL package provides four main classes for creating and manipulating triangulations.
The class CGAL::Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_> models an abstract triangulation: vertices in this class are not embedded in Euclidean space but are only of combinatorial nature.
The class CGAL::Triangulation<TriangulationTraits_, TriangulationDataStructure_> describes an embedded triangulation that has as vertices a given set of points. Methods are provided for the insertion of points in the triangulation, the traversal of various elements of the triangulation, as well as the location of a query point inside the triangulation. The triangulation covers the convex hull of the set of points.
The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_> builds the Delaunay triangulation of a set of points. In a Delaunay triangulation, each face has the so-called Delaunay or empty-ball property: there exists a circumscribing ball whose interior does not contain any vertex of the triangulation.
The class CGAL::Regular_triangulation<RegularTriangulationTraits_, TriangulationDataStructure_> builds the regular triangulation – also known as weighted Delaunay triangulation – of a set of points. A detailed definition of such a triangulation is available in section Regular Triangulations.
In this section, we describe the concept TriangulationDataStructure for which CGAL provides one model class: CGAL::Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_>.
A triangulation data structure can represent an abstract triangulation.
The maximal dimension of a triangulation data structure is a positive integer equal to the maximum dimension a full cell can have. This maximal dimension can be chosen by the user at the creation of the triangulation data structure and can then be obtained using the method tds.maximal_dimension(). A triangulation data structure also knows the current dimension of its full cells, which can be obtained using tds.current_dimension(). In the sequel, let us denote the maximal dimension with \( D \) and the current dimension with \( d \). The inequalities \( -2 \leq d \leq D\) and \( 0 < D\) always hold. The special meaning of negative values for \(d\) is explained below.
The set of faces of a triangulation data structure with current dimension \( d \) forms a triangulation of the topological sphere \( \mathbb{S}^d\).
Two full cells \( \sigma\) and \( \sigma'\) sharing a facet are called neighbors. A full cell has always exactly \( d+1\) neighbors.
Possible values of \(d\) (the current dimension of the triangulation) include
- \(d=-2\)
- This corresponds to an empty triangulation data structure.
- \(d=-1\)
This corresponds to an abstract simplicial complex reduced to a single vertex.
- \(d=0\)
This corresponds to an abstract simplicial complex including two vertices, each corresponding to a full cell; the two full cells being neighbors of each other. This is the unique triangulation of the \( 0\)-sphere.
- \( 0< d \le D\)
- This corresponds to a triangulation of the sphere \( \mathbb{S}^d\).
Triangulation_data_structure ClassWe give here some details about the class Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_> implementing the concept TriangulationDataStructure.
A triangulation data structure explicitly stores its vertices and full cells.
Each vertex stores a reference to one of its incident full cells.
Each full cell \( \sigma \) stores references to its \( d+1\) vertices and neighbors. Its vertices and neighbors are indexed from \( 0\) to \( d \). The indices of its neighbors have the following meaning: the \( i\)-th neighbor of \( \sigma\) is the unique neighbor of \( \sigma\) that does not contain the \( i\)-th vertex of \( \sigma\); in other words, it is the neighbor of \( \sigma\) opposite to the \( i\)-th vertex of \( \sigma\) (Figure Figure 48.1).
The vertices and full cells of the triangulations are accessed through handles and iterators. A handle is a model of the Handle concept, and supports the two dereference operators and operator->.
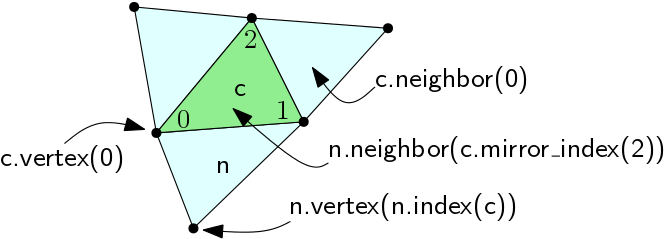
Faces of dimension between 0 and \( d-1 \) can be accessed as subfaces of a full cell, through the nested type Face. The Face instance corresponding to a face \( f \) stores a reference to a full cell c containing \( f \), and the indices of the vertices of c that belong to \( f \).
The Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_> class is designed in such a way that its user can choose
Dimensionality template parameter, TriangulationDSVertex_ template parameter and TriangulationDSFullCell_ template parameter. The last two parameters have default values and are thus not necessary, unless the user needs custom types (see Triangulation_data_structure). The first template parameter, Dimensionality, must be one of the following:
CGAL::Dimension_tag<D> for some integer \( D \). This indicates that the triangulation can store full cells of dimension at most \( D \). The maximum dimension \( D \) is known by the compiler, which triggers some optimizations. CGAL::Dynamic_dimension_tag. In this case, the maximum dimension of the full cells must be passed as an integer argument to an instance constructor (see TriangulationDataStructure). The TriangulationDSVertex_ and TriangulationDSFullCell_ parameters to the class template must be models of the concepts TriangulationDSVertex and TriangulationDSFullCell respectively. CGAL provides models for these concepts: Triangulation_ds_vertex<TriangulationDataStructure_> and Triangulation_ds_full_cell<TriangulationDataStructure_, TriangulationDSFullCellStoragePolicy>, which, as one can see, take the triangulation data structure as a template parameter in order to get access to some nested types in TriangulationDataStructure_.
The default values are CGAL::Triangulation_ds_vertex<TDS> and CGAL::Triangulation_ds_full_cell<TDS> where TDS is the current class Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_>. This creates a circular dependency, which we resolve in the same way as in the CGAL Triangulation_2 and Triangulation_3 packages (see Chapters Chapter_2D_Triangulation_Data_Structure, Chapter_2D_Triangulations, Chapter_3D_Triangulation_Data_Structure, and Chapter_3D_Triangulations). In particular, models of the concepts TriangulationDSVertex and TriangulationDSFullCell must provide a nested template Rebind_TDS which is documented in those two concept's reference manual pages. This mechanism can be used to provide a custom vertex or full cell class. The user is encouraged to read the documentation of the CGAL Triangulation_2 or Triangulation_3 package.
The following examples shows how to construct a triangulation data structure by inserting vertices. Its main interest is that it demonstrates most of the API to insert new vertices into the triangulation.
File triangulation_data_structure_static.cpp
In the previous example, the maximal dimension is fixed at compile time. It is also possible to fix it at run time, as in the next example.
File triangulation_data_structure_dynamic.cpp
This example provides a function for computing the barycentric subdivision of a single full cell c in a triangulation data structure. The other full cells adjacent to c are automatically subdivided to match the subdivision of the full cell c. The barycentric subdivision of c is obtained by enumerating all the faces of c in order of decreasing dimension, from the dimension of c to dimension 1, and inserting a new vertex in each face.
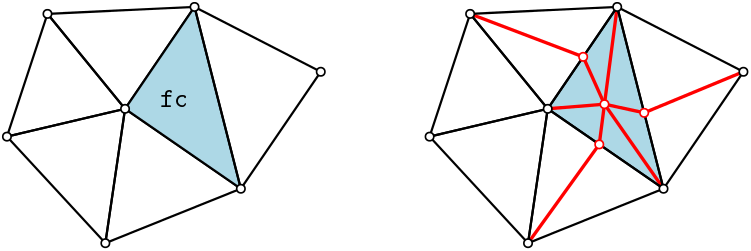
File barycentric_subdivision.cpp
The class CGAL::Triangulation<TriangulationTraits_, TriangulationDataStructure_> maintains a triangulation embedded in Euclidean space. The triangulation covers the convex hull of the input points (the embedded vertices of the triangulation).
To store this triangulation in a triangulation data structure, we turn the set of its faces into a topological sphere by adding a fictitious vertex, called the infinite vertex, as well as infinite simplices incident to boundary faces of the convex hull. Each infinite \( i\)-simplex is incident to the infinite vertex and to an \( (i-1)\)-simplex of the convex hull boundary.
See Chapters 2D Triangulations or 3D Triangulations for more details about infinite vertices and cells.
Methods are provided for the insertion of points in the triangulation, the contraction of faces, the traversal of various elements of the triangulation as well as the location of a query point inside the triangulation.
The ordering of the vertices of a full cell defines an orientation of that full cell. As long as no advanced class method is called, it is guaranteed that all finite full cells have positive orientation. Each infinite full cell is oriented as if its infinite vertex was on the side of the hyperplane supported by its finite facet where there is no other point.
The class CGAL::Triangulation<TriangulationTraits_, TriangulationDataStructure_> stores a model of the concept TriangulationDataStructure that is instantiated with a vertex type that stores a point.
The template parameter TriangulationTraits_ must be a model of the concept TriangulationTraits, which provides the point type as well as various geometric predicates used by the Triangulation class.
The TriangulationTraits concept includes a nested type TriangulationTraits::Dimension. This dimension governs the number of points given as arguments to the predicates. This type is either CGAL::Dimension_tag<D> or CGAL::Dynamic_dimension_tag. In any case, the dimension of the traits must match the maximal dimension of the triangulation data structure.
The template parameter TriangulationDataStructure_ must be a model of the concept TriangulationDataStructure which provides the triangulation data structure as described in the previous section.
The following example shows how to construct a triangulation in which we insert random points. In STEP 1, we generate one hundred random points in \( \mathbb{R}^5\), which we then insert into a triangulation. In STEP 2, we ask the triangulation to construct the set of edges ( \( 1\) dimensional faces) incident to the vertex at infinity. It is easy to see that these edges are in bijection with the vertices on the convex hull of the points. This gives us a handy way to count the convex hull vertices (include files triangulation1.cpp and triangulation2.cpp are given and commented below).
File triangulation.cpp
Remember that a triangulation covers the convex hull of its vertices. Each facet of the convex hull is incident to one finite full cell and one infinite full cell. In fact there is a bijection between the infinite full cells and the facets of the convex hull. If vertices are not in general position, convex hull faces that are not simplices are triangulated. In order to traverse the convex hull facets, there are (at least) two possibilities:
The first is to iterate over the full cells of the triangulation and check if they are infinite or not:
File triangulation1.cpp
A second possibility is to ask the triangulation to gather all the full cells incident to the infinite vertex: they form precisely the set of infinite full cells:
File triangulation2.cpp
One important difference between the two examples above is that the first uses little memory but traverses all the full cells, while the second visits only the infinite full cells but stores handles to them into the potentially big array infinite_full_cells.
The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_> derives from CGAL::Triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_> and represents Delaunay triangulations.
A circumscribing ball of a simplex is a ball having all vertices of the simplex on its boundary. In a Delaunay triangulation, each face has the so-called Delaunay or empty-ball property: there exists a circumscribing ball whose interior does not contain any vertex of the triangulation.
In case of degeneracies (co-spherical points) the triangulation is not uniquely defined. Note however that the CGAL implementation computes a unique triangulation even in these cases.
When a new point p is inserted into a Delaunay triangulation, the full cells whose circumscribing ball contains p are said to be in conflict with point p. Note that the circumscribing ball of an infinite full cell is the empty half-space bounded by the affine hull of the finite facet of this cell. The set of full cells that are in conflict with p form the conflict zone. The full cells in the conflict zone are removed, leaving a hole that contains p. That hole is ``star shaped'' around p and thus is re-triangulated using p as a center vertex.
Delaunay triangulations support insertion of points, removal of vertices, and location of a query point inside the triangulation. Note that inserting a large set of points at once is much faster than inserting the same points one by one.
The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_> derives from CGAL::Triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_>. It thus stores a model of the concept TriangulationDataStructure, which is instantiated with a vertex type that stores a geometric point and allows its retrieval.
The template parameter DelaunayTriangulationTraits_ must be a model of the concept DelaunayTriangulationTraits which provides the geometric Point type as well as various geometric predicates used by the Delaunay_triangulation class. The concept DelaunayTriangulationTraits refines the concept TriangulationTraits by requiring a few additional geometric predicates, necessary for the computation of Delaunay triangulations.
When using a full cell type containing additional custom information, it may be useful to get an efficient access to the full cells that are going to be erased upon the insertion of a new point in the Delaunay triangulation, and to the newly created full cells. The second part of code example below shows how one can have efficient access to both the conflict zone and the created full cells, while still retaining an efficient update of the Delaunay triangulation.
File delaunay_triangulation.cpp
The class CGAL::Regular_triangulation<RegularTriangulationTraits_, TriangulationDataStructure_> derives from CGAL::Triangulation<RegularTriangulationTraits_, TriangulationDataStructure_> and represents regular triangulations.
Regular triangulations are also known as weighted Delaunay triangulations.
Let \( {S}^{(w)}\) be a set of weighted points in \( \mathbb{R}^D\). Let \( {p}^{(w)}=(p,w_p), p\in\mathbb{R}^D, w_p\in\mathbb{R}\) and \( {z}^{(w)}=(z,w_z), z\in\mathbb{R}^D, w_z\in\mathbb{R}\) be two weighted points. A weighted point \( {p}^{(w)}=(p,w_p)\) can also be seen as a sphere of center \( p\) and radius \( \sqrt{w_p}\). The power product (or power distance ) between \( {p}^{(w)}\) and \( {z}^{(w)}\) is defined as
\[ \Pi({p}^{(w)},{z}^{(w)}) = {\|{p-z}\|^2-w_p-w_z} \]
where \( \|{p-z}\|\) is the Euclidean distance between \( p\) and \( z\). \( {p}^{(w)}\) and \( {z}^{(w)}\) are said to be orthogonal if \( \Pi({p}^{(w)},{z}^{(w)}) = 0\).
\(D + 1\) weighted points have a unique common orthogonal weighted point called the power sphere. A sphere \( {z}^{(w)}\) is said to be regular if \( \forall {p}^{(w)}\in{S}^{(w)}, \Pi({p}^{(w)},{z}^{(w)})\geq 0\).
A triangulation of \( {S}^{(w)}\) is regular if the power spheres of all simplices are regular.
Note that as a result, some points can be hidden and do not result in vertices in the triangulation. Those points are discarded and cannot be retrieved.
A weighted point p is said to be in conflict with a simplex s if it has a negative power distance to the power sphere of s.
Regular triangulations support insertion of weighted points, and location of a query point inside the triangulation. Note that inserting a large set of points at once is much faster than inserting the same points one by one.
The class CGAL::Regular_triangulation<RegularTriangulationTraits_, TriangulationDataStructure_> derives from CGAL::Triangulation<RegularTriangulationTraits_, TriangulationDataStructure_>. It thus stores a model of the concept TriangulationDataStructure_ which is instantiated with a vertex type that stores a weighted point and allows its retrieval.
The template parameter RegularTriangulationTraits_ must be a model of the concept RegularTriangulationTraits. It must provide the Weighted_point_d type as well as various geometric predicates used by the Regular_triangulation class. The concept RegularTriangulationTraits refines the concept TriangulationTraits.
This simple example shows how to create a regular triangulation.
File regular_triangulation.cpp
When inserting a batch of points into a Delaunay triangulation, the current implementation starts by spatially sorting the points. Then, for each point to insert, it locates it by walking in the triangulation, using the previously inserted vertex as a "hint". Finally, the point is inserted. In the worst case scenario, without spatial sort, the expected complexity is \( O(n^{\lceil\frac{d}{2}\rceil+1}) \). When the algorithm is run on uniformly distributed points, the localization complexity is \( O(n^{\frac{1}{d}}) \) and the size of the triangulation is \( O(n) \), which gives a complexity of \( O(n^{1+\frac{1}{d}}) \) for the insertion. With spatial sort and random points, one can expect a complexity of \( O(n\log n) \). Please refer to [1] for more details.
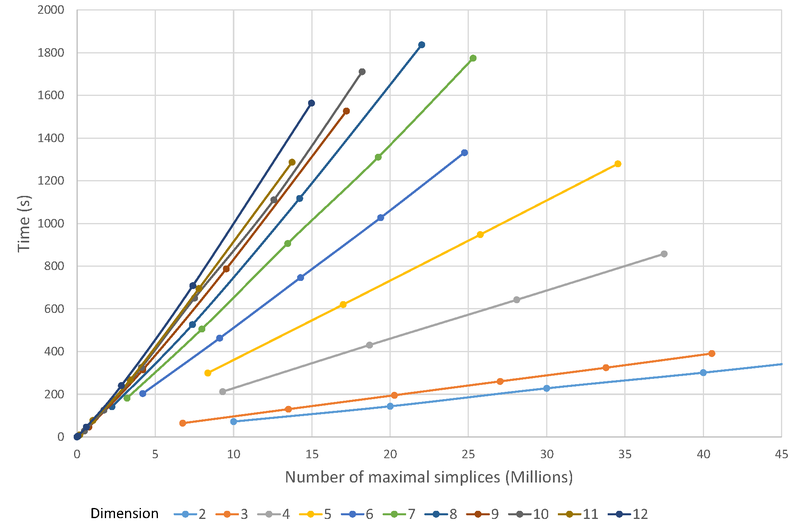
We provide below (Figure 48.3, Figure 48.4 and Figure 48.5) the performance of the Delaunay triangulation on randomly distributed points. The machine used is a PC running Windows 7 64-bits with an Intel Xeon CPU clocked at 2.80 GHz with 32GB of RAM. The program has been compiled with Microsoft Visual C++ 2013 in Release mode.
| Dimension | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 0.003 | 0.007 | 0.03 | 0.14 | 0.56 | 2.7 | 11.3 | 45 | 185 | 686 | 2390 | |
| Memory (MB) | < 1 | < 1 | < 1 | 1 | 3 | 13 | 53 | 182 | 662 | 2187 | 7156 | |
| Number of maximal simplices | 184 | 487 | 1,548 | 5,548 | 19,598 | 67,102 | 230,375 | 715,984 | 2,570,623 | 7,293,293 | 21,235,615 | |
| Number of convex hull facets | 14 | 66 | 308 | 1,164 | 4,410 | 16,974 | 57,589 | 238,406 | 670,545 | 2,574,326 | 8,603,589 | |
| Dimension | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 0.01 | 0.05 | 0.5 | 3.4 | 24 | 183 | 1365 | |
| Memory (MB) | < 1 | < 1 | 2.7 | 14 | 81 | 483 | 2827 | |
| Number of maximal simplices | 1,979 | 6,315 | 25,845 | 122,116 | 596,927 | 3,133,318 | 16,403,337 | |
| Number of convex hull facets | 19 | 138 | 963 | 6,184 | 41,135 | 241,540 | 1,406,797 | |
Starting with the version 2.3 of CGAL, a package written by Susan Hert and Michael Seel was the first able to deal with triangulation and convex hulls in arbitrary dimension. It is deprecated since the version 4.6 of CGAL and this package should be used instead.
This package is heavily inspired by the works of Monique Teillaud and Sylvain Pion (Triangulation_3) and Mariette Yvinec (Triangulation_2). The first version was written by Samuel Hornus. The final version is a joint work by Samuel Hornus, Olivier Devillers and Clément Jamin. In 2017, Clément Jamin added the regular triangulations.
Clément Jamin's work was supported by the Advanced Grant of the European Research Council GUDHI (Geometric Understanding in Higher Dimensions).