3D Triangulation Data Structure Reference

Clément Jamin, Sylvain Pion and Monique Teillaud

This package provides a data structure to store a three-dimensional triangulation that has the topology of a three-dimensional sphere. The package acts as a container for the vertices and cells of the triangulation and provides basic combinatorial operations on the triangulation.

Introduced in: CGAL 2.1
BibTeX: cgal:pt-tds3-23a
License: GPL

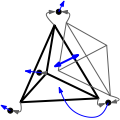
The triangulation data structure is able to represent a triangulation of a topological sphere \( S^d\) of \( \mathbb{R}^{d+1}\), for \( d \in \{-1,0,1,2,3\}\). (See Representation.)

The vertex class of a 3D-triangulation data structure must define a number of types and operations. The requirements that are of geometric nature are required only when the triangulation data structure is used as a layer for the geometric triangulation classes. (See Section Software Design.)

The cell class of a triangulation data structure stores four handles to its four vertices and four handles to its four neighbors. The vertices are indexed 0, 1, 2, and 3 in a consistent order. The neighbor indexed \( i\) lies opposite to vertex i.

In degenerate dimensions, cells are used to store faces of maximal dimension: in dimension 2, each cell represents only one facet of index 3, and 3 edges \( (0,1)\), \( (1,2)\) and \( (2,0)\); in dimension 1, each cell represents one edge \( (0,1)\). (See Section Representation.)

Classified Reference Pages

Concepts

• TriangulationDataStructure_3
• TriangulationDataStructure_3::Cell
• TriangulationDataStructure_3::Cell_data
• TriangulationDataStructure_3::Vertex
• TriangulationDSCellBase_3
• TriangulationDSVertexBase_3

Classes

• CGAL::Triangulation_data_structure_3<Vb,Cb,CT> is a model for the concept of the 3D-triangulation data structure TriangulationDataStructure_3. It is templated by base classes for vertices and cells.

CGAL provides base vertex classes and base cell classes:

• CGAL::Triangulation_ds_cell_base_3<TDS>
• CGAL::Triangulation_ds_vertex_base_3<TDS>

Helper Classes

• CGAL::Triangulation_utils_3 defines operations on the indices of vertices and neighbors within a cell of a triangulation.

Modules
	Concepts
	Classes
	I/O for a Triangulation_data_structure_3