|
CGAL 5.5.2 - 2D Triangulations
|
|
CGAL 5.5.2 - 2D Triangulations
|
#include <CGAL/Triangulation_2.h>
Inherited by CGAL::Constrained_triangulation_2< Traits, Tds, Itag >, CGAL::Delaunay_triangulation_2< Traits, Tds >, and CGAL::Regular_triangulation_2< Traits, Tds >.
The class Triangulation_2 is the basic class designed to handle triangulations of set of points \( { A}\) in the plane.
Such a triangulation has vertices at the points of \( { A}\) and its domain covers the convex hull of \( { A}\). It can be viewed as a planar partition of the plane whose bounded faces are triangular and cover the convex hull of \( { A}\). The single unbounded face of this partition is the complementary of the convex hull of \( { A}\).
In many applications, it is convenient to deal only with triangular faces. Therefore, we add to the triangulation a fictitious vertex, called the infinite vertex and we make each convex hull edge incident to an infinite face having as third vertex the infinite vertex. In that way, each edge is incident to exactly two faces and special cases at the boundary of the convex hull are simpler to deal with.
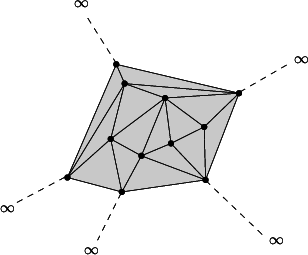
Triangulation_2 implements this point of view and therefore considers the triangulation of the set of points as a set of triangular, finite and infinite faces. Although it is convenient to draw a triangulation as in figure Triangulation_ref_Fig_infinite_vertex, note that the infinite vertex has no significant coordinates and that no geometric predicate can be applied on it or on an infinite face.
A triangulation is a collection of vertices and faces that are linked together through incidence and adjacency relations. Each face give access to its three incident vertices and to its three adjacent faces. Each vertex give access to one of its incident faces.
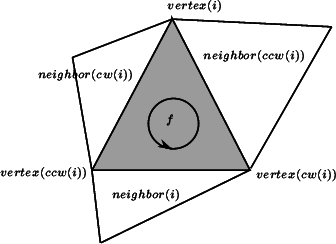
The three vertices of a face are indexed with 0, 1 and 2 in counterclockwise order. The neighbor of a face are also indexed with 0,1,2 in such a way that the neighbor indexed by \( i\) is opposite to the vertex with the same index.
The triangulation class offers two functions int cw(int i) and int ccw(int i) which, given the index of a vertex in a face, compute the index of the next vertex of the same face in clockwise or counterclockwise order. Thus, for example the neighbor neighbor(cw(i)) is the neighbor of f which is next to neighbor(i) turning clockwise around f. The face neighbor(cw(i)) is also the first face encountered after f when turning clockwise around vertex i of f (see Figure Triangulation_ref_Fig_neighbors).
| Traits | is the geometric traits which must be a model of the concept TriangulationTraits_2. |
| Tds | is the triangulation data structure which must be a model of the concept TriangulationDataStructure_2. By default, the triangulation data structure is instantiated by Triangulation_data_structure_2 < Triangulation_vertex_base_2<Gt>, Triangulation_face_base_2<Gt> >. |
Traversal of the Triangulation
A triangulation can be seen as a container of faces and vertices. Therefore the triangulation provides several iterators and circulators that allow to traverse it completely or partially.
Traversal of the Convex Hull
Applied on the infinite vertex the above functions allow to visit the vertices on the convex hull and the infinite edges and faces. Note that a counterclockwise traversal of the vertices adjacent to the infinite vertex is a clockwise traversal of the convex hull.
I/O
The I/O operators are defined for iostream. The format for the iostream is an internal format.
The information output in the iostream is:
The index of an item (vertex of face) is the rank of this item in the output order. When dimension \( <\) 2, the same information is output for faces of maximal dimension instead of faces.
Implementation
Locate is implemented by a line walk from a vertex of the face given as optional parameter (or from a finite vertex of infinite_face() if no optional parameter is given). It takes time \( O(n)\) in the worst case, but only \( O(\sqrt{n})\) on average if the vertices are distributed uniformly at random.
Insertion of a point is done by locating a face that contains the point, and then splitting this face. If the point falls outside the convex hull, the triangulation is restored by flips. Apart from the location, insertion takes a time time \( O(1)\). This bound is only an amortized bound for points located outside the convex hull.
Removal of a vertex is done by removing all adjacent triangles, and re-triangulating the hole. Removal takes time \( O(d^2)\) in the worst case, if \( d\) is the degree of the removed vertex, which is \( O(1)\) for a random vertex.
The face, edge, and vertex iterators on finite features are derived from their counterparts visiting all (finite and infinite) features which are themselves derived from the corresponding iterators of the triangulation data structure.
Related Functions | |
(Note that these are not member functions.) | |
| ostream & | operator<< (ostream &os, const Triangulation_2< Traits, Tds > &T) |
Inserts the triangulation into the stream os. More... | |
| istream & | operator>> (istream &is, const Triangulation_2< Traits, Tds > &T) |
Reads a triangulation from stream is and assigns it to the triangulation. More... | |
Types | |
| typedef Traits | Geom_traits |
| the traits class. | |
| typedef Tds | Triangulation_data_structure |
| the triangulation data structure type. | |
| typedef Traits::Point_2 | Point |
| the point type. | |
| typedef Traits::Segment_2 | Segment |
| the segment type. | |
| typedef Traits::Triangle_2 | Triangle |
| the triangle type. | |
| typedef Tds::Vertex | Vertex |
| the vertex type. | |
| typedef Tds::Face | Face |
| the face type. | |
| typedef Tds::Edge | Edge |
| the edge type. | |
| typedef Tds::size_type | size_type |
| Size type (an unsigned integral type). | |
| typedef Tds::difference_type | difference_type |
| Difference type (a signed integral type). | |
Handles, Iterators, and Circulators | |
The vertices and faces of the triangulations are accessed through handles, iterators and circulators. The handles are models of the concept The edges of the triangulation can also be visited through iterators and circulators, the edge circulators and iterators are also bidirectional and non mutable. In the following, we called infinite any face or edge incident to the infinite vertex and the infinite vertex itself. Any other feature (face, edge or vertex) of the triangulation is said to be finite. Some iterators (the In order to write C++ 11 | |
| enum | Locate_type { VERTEX =0, EDGE, FACE, OUTSIDE_CONVEX_HULL, OUTSIDE_AFFINE_HULL } |
| specifies which case occurs when locating a point in the triangulation. More... | |
| typedef Tds::Vertex_handle | Vertex_handle |
| handle to a vertex. | |
| typedef Tds::Face_handle | Face_handle |
| handle to a face. | |
| typedef Tds::Face_iterator | All_faces_iterator |
| iterator over all faces. | |
| typedef Tds::Edge_iterator | All_edges_iterator |
| iterator over all edges. | |
| typedef Tds::Vertex_iterator | All_vertices_iterator |
| iterator over all vertices. | |
| typedef unspecified_type | Finite_faces_iterator |
| iterator over finite faces. | |
| typedef unspecified_type | Finite_edges_iterator |
| iterator over finite edges. | |
| typedef unspecified_type | Finite_vertices_iterator |
| iterator over finite vertices. | |
| typedef unspecified_type | Point_iterator |
| iterator over the points corresponding to the finite vertices of the triangulation. | |
| typedef Iterator_range< unspecified_type > | All_face_handles |
range type for iterating over all faces (including infinite faces), with a nested type iterator that has as value type Face_handle. | |
| typedef Iterator_range< All_edges_iterator > | All_edges |
| range type for iterating over all edges (including infinite ones). | |
| typedef Iterator_range< unspecified_type > | All_vertex_handles |
range type for iterating over all vertices (including the infinite vertex), with a nested type iterator that has as value type Vertex_handle. | |
| typedef Iterator_range< unspecified_type > | Finite_face_handles |
range type for iterating over finite faces, with a nested type iterator that has as value type Face_handle. | |
| typedef Iterator_range< Finite_edges_iterator > | Finite_edges |
| range type for iterating over finite edges. | |
| typedef Iterator_range< unspecified_type > | Finite_vertex_handles |
range type for iterating over finite vertices, with a nested type iterator that has as value type Vertex_handle. | |
| typedef Iterator_range< Point_iterator > | Points |
| range type for iterating over the points of the finite vertices. | |
| typedef unspecified_type | Line_face_circulator |
| circulator over all faces intersected by a line. | |
| typedef unspecified_type | Face_circulator |
| circulator over all faces incident to a given vertex. | |
| typedef unspecified_type | Edge_circulator |
| circulator over all edges incident to a given vertex. | |
| typedef unspecified_type | Vertex_circulator |
| circulator over all vertices incident to a given vertex. | |
Creation | |
| Triangulation_2 (const Traits >=Traits()) | |
| Introduces an empty triangulation. | |
| Triangulation_2 (const Triangulation_2 &tr) | |
| Copy constructor. More... | |
| template<class InputIterator > | |
| Triangulation_2 (InputIterator first, InputIterator last, const Traits >=Traits()) | |
| Equivalent to constructing an empty triangulation with the optional traits class argument and calling insert(first,last). | |
| Triangulation_2 | operator= (const Triangulation_2< Traits, Tds > &tr) |
| Assignment. More... | |
| void | swap (Triangulation_2 &tr) |
The triangulations tr and *this are swapped. More... | |
| void | clear () |
| Deletes all faces and finite vertices resulting in an empty triangulation. | |
Access Functions | |
| int | dimension () const |
| Returns the dimension of the convex hull. | |
| size_type | number_of_vertices () const |
| Returns the number of finite vertices. | |
| size_type | number_of_faces () const |
| Returns the number of finite faces. | |
| Face_handle | infinite_face () const |
| a face incident to the infinite vertex. | |
| Vertex_handle | infinite_vertex () const |
| the infinite vertex. | |
| Vertex_handle | finite_vertex () const |
| a vertex distinct from the infinite vertex. | |
| const Geom_traits & | geom_traits () const |
| Returns a const reference to the triangulation traits object. | |
| const TriangulationDataStructure_2 & | tds () const |
| Returns a const reference to the triangulation data structure. | |
Non const access | |
| |
| TriangulationDataStructure_2 & | tds () |
| Returns a reference to the triangulation data structure. | |
Predicates | |
The class | |
| bool | is_infinite (Vertex_handle v) const |
true iff v is the infinite vertex. | |
| bool | is_infinite (Face_handle f) const |
true iff face f is infinite. | |
| bool | is_infinite (Face_handle f, int i) const |
true iff edge (f,i) is infinite. | |
| bool | is_infinite (Edge e) const |
true iff edge e is infinite. | |
| bool | is_infinite (Edge_circulator ec) const |
true iff edge *ec is infinite. | |
| bool | is_infinite (All_edges_iterator ei) const |
true iff edge *ei is infinite. | |
| bool | is_edge (Vertex_handle va, Vertex_handle vb) |
true if there is an edge having va and vb as vertices. | |
| bool | is_edge (Vertex_handle va, Vertex_handle vb, Face_handle &fr, int &i) |
| as above. More... | |
| bool | includes_edge (Vertex_handle va, Vertex_handle vb, Vertex_handle &vbr, Face_handle &fr, int &i) |
true if the line segment from va to vb includes an edge e incident to va. More... | |
| bool | is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3) |
true if there is a face having v1, v2 and v3 as vertices. | |
| bool | is_face (Vertex_handle v1, Vertex_handle v2, Vertex_handle v3, Face_handle &fr) |
| as above. More... | |
Queries | |
The class It also provides methods to locate a point with respect to a given finite face of the triangulation. | |
| Face_handle | locate (const Point &query, Face_handle f=Face_handle()) const |
If the point query lies inside the convex hull of the points, a face that contains the query in its interior or on its boundary is returned. More... | |
| Face_handle | inexact_locate (const Point &query, Face_handle start=Face_handle()) const |
Same as locate() but uses inexact predicates. More... | |
| Face_handle | locate (const Point &query, Locate_type <, int &li, Face_handle h=Face_handle()) const |
| Same as above. More... | |
| Oriented_side | oriented_side (Face_handle f, const Point &p) const |
Returns on which side of the oriented boundary of f lies the point p. More... | |
| Oriented_side | side_of_oriented_circle (Face_handle f, const Point &p) |
Returns on which side of the circumcircle of face f lies the point p. More... | |
Modifiers | |
The following operations are guaranteed to lead to a valid triangulation when they are applied on a valid triangulation. 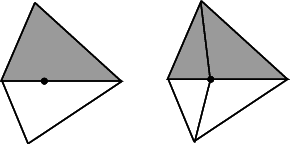
Insertion of a point on an edge. 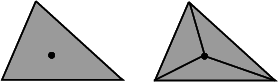
Insertion in a face. 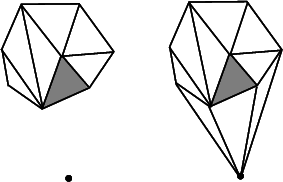
Insertion outside the convex hull. 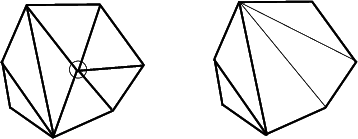
Removal. | |
| void | flip (Face_handle f, int i) |
Exchanges the edge incident to f and f->neighbor(i) with the other diagonal of the quadrilateral formed by f and f->neighbor(i). More... | |
| Vertex_handle | insert (const Point &p, Face_handle f=Face_handle()) |
Inserts point p in the triangulation and returns the corresponding vertex. More... | |
| Vertex_handle | insert (const Point &p, Locate_type lt, Face_handle loc, int li) |
Same as above except that the location of the point p to be inserted is assumed to be given by (lt,loc,i) (see the description of the locate method above.) | |
| Vertex_handle | push_back (const Point &p) |
Equivalent to insert(p). | |
| template<class PointInputIterator > | |
| std::ptrdiff_t | insert (PointInputIterator first, PointInputIterator last) |
Inserts the points in the range [first,last) in the given order, and returns the number of inserted points. More... | |
| template<class PointWithInfoInputIterator > | |
| std::ptrdiff_t | insert (PointWithInfoInputIterator first, PointWithInfoInputIterator last) |
inserts the points in the iterator range [first,last) in the given order, and returns the number of inserted points. More... | |
| void | remove (Vertex_handle v) |
| Removes the vertex from the triangulation. More... | |
| Vertex_handle | move_if_no_collision (Vertex_handle v, const Point &p) |
If there is not already another vertex placed on p, the triangulation is modified such that the new position of vertex v is p, and v is returned. More... | |
| Vertex_handle | move (Vertex_handle v, const Point &p) |
If there is no collision during the move, this function is the same as move_if_no_collision . More... | |
Specialized Modifiers | |
The following member functions offer more specialized versions of the insertion or removal operations to be used when one knows to be in the corresponding case. | |
| Vertex_handle | insert_first (const Point &p) |
| Inserts the first finite vertex . | |
| Vertex_handle | insert_second (const Point &p) |
| Inserts the second finite vertex . | |
| Vertex_handle | insert_in_face (const Point &p, Face_handle f) |
Inserts vertex v in face f. More... | |
| Vertex_handle | insert_in_edge (const Point &p, Face_handle f, int i) |
Inserts vertex v in edge i of f. More... | |
| Vertex_handle | insert_outside_convex_hull (const Point &p, Face_handle f) |
| Inserts a point which is outside the convex hull but in the affine hull. More... | |
| Vertex_handle | insert_outside_affine_hull (const Point &p) |
| Inserts a point which is outside the affine hull. | |
| void | remove_degree_3 (Vertex_handle v) |
| Removes a vertex of degree three. More... | |
| void | remove_second (Vertex_handle v) |
| Removes the before last finite vertex. | |
| void | remove_first (Vertex_handle v) |
| Removes the last finite vertex. | |
| template<class EdgeIt > | |
| Vertex_handle | star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end) |
creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end). More... | |
| template<class EdgeIt , class FaceIt > | |
| Vertex_handle | star_hole (Point p, EdgeIt edge_begin, EdgeIt edge_end, FaceIt face_begin, FaceIt face_end) |
same as above, except that the algorithm first recycles faces in the sequence [face_begin, face_end) and create new ones only when the sequence is exhausted. More... | |
Finite Face, Edge and Vertex Iterators | |
The following iterators allow respectively to visit finite faces, finite edges and finite vertices of the triangulation. These iterators are non mutable, bidirectional and their value types are respectively | |
| Finite_vertices_iterator | finite_vertices_begin () const |
| Starts at an arbitrary finite vertex. | |
| Finite_vertices_iterator | finite_vertices_end () const |
| Past-the-end iterator. | |
| Finite_edges_iterator | finite_edges_begin () const |
| Starts at an arbitrary finite edge. | |
| Finite_edges_iterator | finite_edges_end () const |
| Past-the-end iterator. | |
| Finite_faces_iterator | finite_faces_begin () const |
| Starts at an arbitrary finite face. | |
| Finite_faces_iterator | finite_faces_end () const |
| Past-the-end iterator. | |
| Point_iterator | points_begin () const |
| Point_iterator | points_end () const |
| Past-the-end iterator. | |
| Finite_vertex_handles | finite_vertex_handles () const |
| returns a range of iterators over finite vertices. More... | |
| Finite_edges | finite_edges () const |
| returns a range of iterators over finite edges. | |
| Finite_face_handles | finite_face_handles () const |
| returns a range of iterators over finite faces. More... | |
| Points | points () const |
| returns a range of iterators over the points of finite vertices. | |
All Face, Edge and Vertex Iterators | |
The following iterators allow respectively to visit all (finite or infinite) faces, edges and vertices of the triangulation. These iterators are non mutable, bidirectional and their value types are respectively | |
| All_vertices_iterator | all_vertices_begin () const |
| Starts at an arbitrary vertex. | |
| All_vertices_iterator | all_vertices_end () const |
| Past-the-end iterator. | |
| All_edges_iterator | all_edges_begin () const |
| Starts at an arbitrary edge. | |
| All_edges_iterator | all_edges_end () const |
| Past-the-end iterator. | |
| All_faces_iterator | all_faces_begin () const |
| Starts at an arbitrary face. | |
| All_faces_iterator | all_faces_end () const |
| Past-the-end iterator. | |
| All_vertex_handles | all_vertex_handles () const |
| returns a range of iterators over all vertices. More... | |
| All_edges | all_edges () const |
| returns a range of iterators over all edges. | |
| All_face_handles | all_face_handles () const |
| returns a range of iterators over all faces. More... | |
Line Face Circulator | |
The triangulation defines a circulator that allows to visit all faces that are intersected by a line. A face
The circulator has a singular value if the line 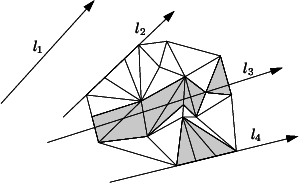
The line face circulator. A line face circulator is invalidated if the face the circulator refers to is changed. | |
| Line_face_circulator | line_walk (const Point &p, const Point &q, Face_handle f=Face_handle()) const |
This function returns a circulator that allows to visit the faces intersected by the line pq. More... | |
Face, Edge and Vertex Circulators | |
The triangulation also provides circulators that allows to visit respectively all faces or edges incident to a given vertex or all vertices adjacent to a given vertex. These circulators are non-mutable and bidirectional. The | |
| Face_circulator | incident_faces (Vertex_handle v) const |
Starts at an arbitrary face incident to v. | |
| Face_circulator | incident_faces (Vertex_handle v, Face_handle f) const |
Starts at face f. More... | |
| Edge_circulator | incident_edges (Vertex_handle v) const |
Starts at an arbitrary edge incident to v. | |
| Edge_circulator | incident_edges (Vertex_handle v, Face_handle f) const |
Starts at the first edge of f incident to v, in counterclockwise order around v. More... | |
| Vertex_circulator | incident_vertices (Vertex_handle v) const |
Starts at an arbitrary vertex incident to v. | |
| Vertex_circulator | incident_vertices (Vertex_handle v, Face_handle f) |
Starts at the first vertex of f adjacent to v in counterclockwise order around v. More... | |
Traversal Between Adjacent Faces | |
| Vertex_handle | mirror_vertex (Face_handle f, int i) const |
returns the vertex of the \( i^{th}\) neighbor of f that is opposite to f. More... | |
| int | mirror_index (Face_handle f, int i) const |
returns the index of f in its \( i^{th}\) neighbor. More... | |
| Edge | mirror_edge (Edge e) const |
| returns the same edge seen from the other adjacent face. More... | |
Miscellaneous | |
| int | ccw (int i) const |
| Returns \( i+1\) modulo 3. More... | |
| int | cw (int i) const |
| Returns \( i+2\) modulo 3. More... | |
| Triangle | triangle (Face_handle f) const |
Returns the triangle formed by the three vertices of f. More... | |
| Segment | segment (Face_handle f, int i) const |
Returns the line segment formed by the vertices ccw(i) and cw(i) of face f. More... | |
| Segment | segment (const Edge &e) const |
Returns the line segment corresponding to edge e. More... | |
| Segment | segment (const Edge_circulator &ec) const |
Returns the line segment corresponding to edge *ec. More... | |
| Segment | segment (const Edge_iterator &ei) const |
Returns the line segment corresponding to edge *ei. More... | |
| Point | circumcenter (Face_handle f) const |
| Compute the circumcenter of the face pointed to by f. More... | |
Setting | |
| void | set_infinite_vertex (const Vertex_handle &v) |
| This is an advanced function. More... | |
Checking | |
Advanced
The responsibility of keeping a valid triangulation belongs to the users if advanced operations are used. Obviously the advanced user, who implements higher levels operations may have to make a triangulation invalid at some times. The following method is provided to help the debugging. | |
| bool | is_valid (bool verbose=false, int level=0) const |
| Checks the combinatorial validity of the triangulation and also the validity of its geometric embedding. More... | |
Additional Inherited Members | |
 Public Member Functions inherited from CGAL::Triangulation_cw_ccw_2 Public Member Functions inherited from CGAL::Triangulation_cw_ccw_2 | |
| Triangulation_cw_ccw_2 () | |
| default constructor. | |
| int | ccw (const int i) const |
returns the index of the neighbor or vertex that is next to the neighbor or vertex with index i in counterclockwise order around a face. | |
| int | cw (const int i) const |
returns the index of the neighbor or vertex that is next to the neighbor or vertex with index i in counterclockwise order around a face. | |
| enum CGAL::Triangulation_2::Locate_type |
specifies which case occurs when locating a point in the triangulation.
CGAL::Triangulation_2<Traits,Tds> | CGAL::Triangulation_2< Traits, Tds >::Triangulation_2 | ( | const Triangulation_2< Traits, Tds > & | tr | ) |
Copy constructor.
All the vertices and faces are duplicated. After the copy, *this and tr refer to different triangulations: if tr is modified, *this is not.
| All_face_handles CGAL::Triangulation_2< Traits, Tds >::all_face_handles | ( | ) | const |
returns a range of iterators over all faces.
All_faces_iterator is Face, the value type of All_face_handles::iterator is Face_handle. | All_vertex_handles CGAL::Triangulation_2< Traits, Tds >::all_vertex_handles | ( | ) | const |
returns a range of iterators over all vertices.
All_vertices_iterator is Vertex, the value type of All_vertex_handles::iterator is Vertex_handle. | int CGAL::Triangulation_2< Traits, Tds >::ccw | ( | int | i | ) | const |
Returns \( i+1\) modulo 3.
| Point CGAL::Triangulation_2< Traits, Tds >::circumcenter | ( | Face_handle | f | ) | const |
Compute the circumcenter of the face pointed to by f.
This function is available only if the corresponding function is provided in the geometric traits.
| int CGAL::Triangulation_2< Traits, Tds >::cw | ( | int | i | ) | const |
Returns \( i+2\) modulo 3.
| Finite_face_handles CGAL::Triangulation_2< Traits, Tds >::finite_face_handles | ( | ) | const |
returns a range of iterators over finite faces.
Finite_faces_iterator is Face, the value type of Finite_face_handles::iterator is Face_handle. | Finite_vertex_handles CGAL::Triangulation_2< Traits, Tds >::finite_vertex_handles | ( | ) | const |
returns a range of iterators over finite vertices.
Finite_vertices_iterator is Vertex, the value type of Finite_vertex_handles::iterator is Vertex_handle. | void CGAL::Triangulation_2< Traits, Tds >::flip | ( | Face_handle | f, |
| int | i | ||
| ) |
Exchanges the edge incident to f and f->neighbor(i) with the other diagonal of the quadrilateral formed by f and f->neighbor(i).
f and f->neighbor(i) are finite faces and their union form a convex quadrilateral. | Edge_circulator CGAL::Triangulation_2< Traits, Tds >::incident_edges | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) | const |
Starts at the first edge of f incident to v, in counterclockwise order around v.
f is incident to vertex v. | Face_circulator CGAL::Triangulation_2< Traits, Tds >::incident_faces | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) | const |
Starts at face f.
f is incident to vertex v. | Vertex_circulator CGAL::Triangulation_2< Traits, Tds >::incident_vertices | ( | Vertex_handle | v, |
| Face_handle | f | ||
| ) |
Starts at the first vertex of f adjacent to v in counterclockwise order around v.
f is incident to vertex v. | bool CGAL::Triangulation_2< Traits, Tds >::includes_edge | ( | Vertex_handle | va, |
| Vertex_handle | vb, | ||
| Vertex_handle & | vbr, | ||
| Face_handle & | fr, | ||
| int & | i | ||
| ) |
true if the line segment from va to vb includes an edge e incident to va.
If true, vbr becomes the other vertex of e, e is the edge (fr,i) where fr is a handle to the face incident to e and on the right side e oriented from va to vb.
| Face_handle CGAL::Triangulation_2< Traits, Tds >::inexact_locate | ( | const Point & | query, |
| Face_handle | start = Face_handle() |
||
| ) | const |
Same as locate() but uses inexact predicates.
This function returns a handle on a face that is a good approximation of the exact location of query, while being faster. Note that it may return a handle on a face whose interior does not contain query. When the triangulation has dimension smaller than 2, start is returned.
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::insert | ( | const Point & | p, |
| Face_handle | f = Face_handle() |
||
| ) |
Inserts point p in the triangulation and returns the corresponding vertex.
If point p coincides with an already existing vertex, this vertex is returned and the triangulation remains unchanged.
If point p is on an edge, the two incident faces are split in two.
If point p is strictly inside a face of the triangulation, the face is split in three.
If point p is strictly outside the convex hull, p is linked to all visible points on the convex hull to form the new triangulation.
At last, if p is outside the affine hull (in case of degenerate 1-dimensional or 0-dimensional triangulations), p is linked all the other vertices to form a triangulation whose dimension is increased by one. The last argument f is an indication to the underlying locate algorithm of where to start.
| std::ptrdiff_t CGAL::Triangulation_2< Traits, Tds >::insert | ( | PointInputIterator | first, |
| PointInputIterator | last | ||
| ) |
Inserts the points in the range [first,last) in the given order, and returns the number of inserted points.
| PointInputIterator | must be an input iterator with value type Point. |
| std::ptrdiff_t CGAL::Triangulation_2< Traits, Tds >::insert | ( | PointWithInfoInputIterator | first, |
| PointWithInfoInputIterator | last | ||
| ) |
inserts the points in the iterator range [first,last) in the given order, and returns the number of inserted points.
Given a pair (p,i), the vertex v storing p also stores i, that is v.point() == p and v.info() == i. If several pairs have the same point, only one vertex is created, and one of the objects of type Vertex::Info will be stored in the vertex.
Vertex must be model of the concept TriangulationVertexBaseWithInfo_2.| PointWithInfoInputIterator | must be an input iterator with the value type std::pair<Point,Vertex::Info>. |
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::insert_in_edge | ( | const Point & | p, |
| Face_handle | f, | ||
| int | i | ||
| ) |
Inserts vertex v in edge i of f.
v lies on the edge opposite to the vertex i of face f. | Vertex_handle CGAL::Triangulation_2< Traits, Tds >::insert_in_face | ( | const Point & | p, |
| Face_handle | f | ||
| ) |
Inserts vertex v in face f.
Face f is modified, two new faces are created.
v lies inside face f. | Vertex_handle CGAL::Triangulation_2< Traits, Tds >::insert_outside_convex_hull | ( | const Point & | p, |
| Face_handle | f | ||
| ) |
Inserts a point which is outside the convex hull but in the affine hull.
f points to a face which is a proof of the location ofp, see the description of the locate method above. | bool CGAL::Triangulation_2< Traits, Tds >::is_edge | ( | Vertex_handle | va, |
| Vertex_handle | vb, | ||
| Face_handle & | fr, | ||
| int & | i | ||
| ) |
as above.
In addition, if true is returned, the edge with vertices va and vb is the edge e=(fr,i) where fr is a handle to the face incident to e and on the right side of e oriented from va to vb.
| bool CGAL::Triangulation_2< Traits, Tds >::is_face | ( | Vertex_handle | v1, |
| Vertex_handle | v2, | ||
| Vertex_handle | v3, | ||
| Face_handle & | fr | ||
| ) |
as above.
In addition, if true is returned, fr is a handle to the face with v1, v2 and v3 as vertices.
| bool CGAL::Triangulation_2< Traits, Tds >::is_valid | ( | bool | verbose = false, |
| int | level = 0 |
||
| ) | const |
Checks the combinatorial validity of the triangulation and also the validity of its geometric embedding.
This method is mainly a debugging help for the users of advanced features.
| Line_face_circulator CGAL::Triangulation_2< Traits, Tds >::line_walk | ( | const Point & | p, |
| const Point & | q, | ||
| Face_handle | f = Face_handle() |
||
| ) | const |
This function returns a circulator that allows to visit the faces intersected by the line pq.
If there is no such face the circulator has a singular value.
The starting point of the circulator is the face f, or the first finite face traversed by l , if f is omitted.
The circulator wraps around the infinite vertex: after the last traversed finite face, it steps through the infinite face adjacent to this face then through the infinite face adjacent to the first traversed finite face then through the first finite traversed face again.
p and q must be different points. f != nullptr, it must point to a finite face and the point p must be inside or on the boundary of f. | Face_handle CGAL::Triangulation_2< Traits, Tds >::locate | ( | const Point & | query, |
| Face_handle | f = Face_handle() |
||
| ) | const |
If the point query lies inside the convex hull of the points, a face that contains the query in its interior or on its boundary is returned.
If the point query lies outside the convex hull of the triangulation but in the affine hull, the returned face is an infinite face which is a proof of the point's location:
query lies to the left of the oriented line \( pq\) (the rest of the triangulation lying to the right of this line).query and the triangulation lie on either side of p.If the point query lies outside the affine hull, the returned Face_handle is nullptr.
The optional Face_handle argument, if provided, is used as a hint of where the locate process has to start its search.
| Face_handle CGAL::Triangulation_2< Traits, Tds >::locate | ( | const Point & | query, |
| Locate_type & | lt, | ||
| int & | li, | ||
| Face_handle | h = Face_handle() |
||
| ) | const |
Same as above.
Additionally, the parameters lt and li describe where the query point is located. The variable lt is set to the locate type of the query. If lt==VERTEX the variable li is set to the index of the vertex, and if lt==EDGE li is set to the index of the vertex opposite to the edge. Be careful that li has no meaning when the query type is FACE, OUTSIDE_CONVEX_HULL, or OUTSIDE_AFFINE_HULL or when the triangulation is \( 0\)-dimensional.
| Edge CGAL::Triangulation_2< Traits, Tds >::mirror_edge | ( | Edge | e | ) | const |
returns the same edge seen from the other adjacent face.
| int CGAL::Triangulation_2< Traits, Tds >::mirror_index | ( | Face_handle | f, |
| int | i | ||
| ) | const |
returns the index of f in its \( i^{th}\) neighbor.
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::mirror_vertex | ( | Face_handle | f, |
| int | i | ||
| ) | const |
returns the vertex of the \( i^{th}\) neighbor of f that is opposite to f.
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::move | ( | Vertex_handle | v, |
| const Point & | p | ||
| ) |
If there is no collision during the move, this function is the same as move_if_no_collision .
Otherwise, v is removed and the vertex at point p is returned.
v must be finite. | Vertex_handle CGAL::Triangulation_2< Traits, Tds >::move_if_no_collision | ( | Vertex_handle | v, |
| const Point & | p | ||
| ) |
If there is not already another vertex placed on p, the triangulation is modified such that the new position of vertex v is p, and v is returned.
Otherwise, the triangulation is not modified and the vertex at point p is returned.
v must be finite. | Triangulation_2 CGAL::Triangulation_2< Traits, Tds >::operator= | ( | const Triangulation_2< Traits, Tds > & | tr | ) |
Assignment.
All the vertices and faces are duplicated. After the assignment, *this and tr refer to different triangulations: if tr is modified, *this is not.
| Oriented_side CGAL::Triangulation_2< Traits, Tds >::oriented_side | ( | Face_handle | f, |
| const Point & | p | ||
| ) | const |
Returns on which side of the oriented boundary of f lies the point p.
f is finite. | void CGAL::Triangulation_2< Traits, Tds >::remove | ( | Vertex_handle | v | ) |
Removes the vertex from the triangulation.
The created hole is re-triangulated.
v must be finite. | void CGAL::Triangulation_2< Traits, Tds >::remove_degree_3 | ( | Vertex_handle | v | ) |
Removes a vertex of degree three.
Two of the incident faces are destroyed, the third one is modified.
v is a finite vertex with degree three. | Segment CGAL::Triangulation_2< Traits, Tds >::segment | ( | Face_handle | f, |
| int | i | ||
| ) | const |
Returns the line segment formed by the vertices ccw(i) and cw(i) of face f.
ccw(i) and cw(i) of f are finite. | Segment CGAL::Triangulation_2< Traits, Tds >::segment | ( | const Edge & | e | ) | const |
Returns the line segment corresponding to edge e.
e is a finite edge. | Segment CGAL::Triangulation_2< Traits, Tds >::segment | ( | const Edge_circulator & | ec | ) | const |
Returns the line segment corresponding to edge *ec.
*ec is a finite edge. | Segment CGAL::Triangulation_2< Traits, Tds >::segment | ( | const Edge_iterator & | ei | ) | const |
Returns the line segment corresponding to edge *ei.
*ei is a finite edge. | void CGAL::Triangulation_2< Traits, Tds >::set_infinite_vertex | ( | const Vertex_handle & | v | ) |
This is an advanced function.
This method is meant to be used only if you have done a low-level operation on the underlying tds that invalidated the infinite vertex. Sets the infinite vertex.
| Oriented_side CGAL::Triangulation_2< Traits, Tds >::side_of_oriented_circle | ( | Face_handle | f, |
| const Point & | p | ||
| ) |
Returns on which side of the circumcircle of face f lies the point p.
The circle is assumed to be counterclockwise oriented, so its positive side correspond to its bounded side. This predicate is available only if the corresponding predicates on points is provided in the geometric traits class.
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::star_hole | ( | Point | p, |
| EdgeIt | edge_begin, | ||
| EdgeIt | edge_end | ||
| ) |
creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end).
Returns a handle to the new vertex.
This function is intended to be used in conjunction with the find_conflicts() member functions of Delaunay and constrained Delaunay triangulations to perform insertions.
| Vertex_handle CGAL::Triangulation_2< Traits, Tds >::star_hole | ( | Point | p, |
| EdgeIt | edge_begin, | ||
| EdgeIt | edge_end, | ||
| FaceIt | face_begin, | ||
| FaceIt | face_end | ||
| ) |
same as above, except that the algorithm first recycles faces in the sequence [face_begin, face_end) and create new ones only when the sequence is exhausted.
This function is intended to be used in conjunction with the find_conflicts() member functions of Delaunay and constrained Delaunay triangulations to perform insertions.
| void CGAL::Triangulation_2< Traits, Tds >::swap | ( | Triangulation_2< Traits, Tds > & | tr | ) |
The triangulations tr and *this are swapped.
This method should be used instead of assignment of copy construtor. if tr is deleted after that.
| Triangle CGAL::Triangulation_2< Traits, Tds >::triangle | ( | Face_handle | f | ) | const |
Returns the triangle formed by the three vertices of f.
|
related |
Inserts the triangulation into the stream os.
Point.
|
related |
Reads a triangulation from stream is and assigns it to the triangulation.
Point.