
 |
Multiplying the transformation matrix by a scalar does not change the represented transformation. Therefore, any transformation represented by a matrix with rational entries can be represented by a transformation matrix with integer entries as well. (Multiply the matrix with the common denominator of the rational entries.) Hence, it is sufficient to use the number type Kernel::RT to represent the entries of the transformation matrix.
CGAL offers several specialized affine transformations. Different constructors are provided to create them. They are parameterized with a symbolic name to denote the transformation type, followed by additional parameters. The symbolic name tags solve ambiguities in the function overloading and they make the code more readable, i.e., what type of transformation is created.
In three-dimensional space we have a matrix . Entries , , and are always zero and therefore do not appear in the constructors.
|
| |||
|
introduces an identity transformation.
| |||
|
| |||
|
introduces a translation by a vector .
| |||
| |||
|
introduces a scaling by a scale factor .
| |||
| |||
introduces a general affine transformation of the matrix
form 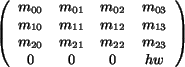 . The part . The part
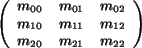 defines the scaling and rotational part of the transformation,
while the vector
defines the scaling and rotational part of the transformation,
while the vector  contains the translational part. contains the translational part.
| |||
| |||
introduces a general linear transformation of the
matrix form 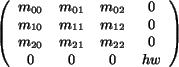 , i.e. an affine
transformation without translational part. , i.e. an affine
transformation without translational part.
| |||
Each class Class_3<Kernel> representing a geometric object in 3D has a member function:
Class_3<Kernel> transform(Aff_transformation_3<Kernel> t).
The transformation classes provide a member function transform() for points, vectors, directions, and planes:
|
|
| |
|
|
| |
|
| ||
|
| ||
|
|
| |
CGAL provides four function operators for these member functions:
|
|
| |
|
|
| |
|
| ||
|
| ||
|
|
| |
|
| ||
|
| composes two affine transformations. | |
|
| ||
|
| gives the inverse transformation. | |
|
|
| returns true, if the transformation is not reflecting, i.e. the determinant of the involved linear transformation is non-negative. |
|
|
| returns true, if the transformation is reflecting. |
The matrix entries of a matrix representation of a Aff_transformation_3<Kernel> can be accessed trough the following member functions:
|
|
| |
|
|
| |
| returns entry in a matrix representation in which is 1. | ||
|
|
| |
|
|
| |
| returns entry in some fixed matrix representation. | ||
For affine transformations no I/O operators are defined.