Chapter 13
Nef Polyhedra embedded on the Sphere

13.1   Introduction

Nef polyhedra are defined as a subset of the d-dimensional space obtained by a finite number of set complement and set intersection operations on halfspaces.

Due to the fact that all other binary set operations like union, difference and symmetric difference can be reduced to intersection and complement calculations, Nef polyhedra are also closed under those operations. Also, Nef polyhedra are closed under topological unary set operations. Given a Nef polyhedron one can determine its interior, its boundary, and its closure.

Figure:  Two spherical Nef polyhedra. A closed halfspace on the left and a complex polyhedron on the right. The different colors indicate selected and unselected regions, lines and points.

Additionally, a d-dimensional Nef polyhedron has the property, that its boundary is a (d-1)-dimensional Nef polyhedron. This property can be used as a way to represent 3-dimensional Nef polyhedra by means of planar Nef polyhedra. This is done by intersecting the neighborhood of a vertex in a 3D Nef polyhedron with an $$-sphere. The result is a planar Nef polyhedron embedded on the sphere.

The intersection of a halfspace going through the center of the $$-sphere, with the $$-sphere, results in a halfsphere which is bounded by a great circle. A binary operation of two halfspheres cuts the great circles into great arcs.

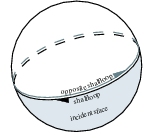
The incidence structure of planar Nef polyhedra can be reused. The items are denoted as $$svertex, $$shalfedge and $$sface, analogous to their counterparts in Nef_polyhedron_S2. Additionally, there is the shalfloop reprsenting the great circles. The incidences are illustrated in the figure above.

13.2   Restricted Spherical Geometry

We introduce geometric objects that are part of the spherical surface $$S₂ and operations on them. We define types Sphere_point, Sphere_circle, Sphere_segment, and Sphere_direction. Sphere_points are points on $$S₂, Sphere_circles are oriented great circles of $$S₂, Sphere_segments are oriented parts of Sphere_circles bounded by a pair of Sphere_points, and Sphere_directions are directions that are part of great circles. (a direction is usually defined to be a vector without length, that floats around in its underlying space and can be used to specify a movement at any point of the underlying space; in our case we use directions only at points that are part of the great circle that underlies also the direction.)

Note that we have to consider special geometric properties of the objects. For example two points that are part of a great circle define two Sphere_segments, and two arbitrary Sphere_segments can intersect in two points.

If we restrict our geometric objects to a so-called perfect hemisphere of $$S₂¹ then the restricted objects behave like in classical geometry, e.g., two points define exactly one segment, two segments intersect in at most one interior point (non-degenerately), or three non-cocircular sphere points can be qualified as being positively or negatively oriented.

13.3   Example Programs

13.3.1   First Example

In this first example Nef_polyhedron_S2 is parametrized with a CGAL Kernel as traits class. The types comprising the spherical geometry can be retrieved from the type Nef_polyhedron_S2<Traits> as is done in the example with the type Sphere_circle. Then three Nef polyhedra are created: $$N1 is a halfsphere including the boundary, $$N2 is another halfsphere without the boundary, and $$N3 is the intersection of $$N1 and $$N2.

// examples/Nef_S2/simple.C

#include <CGAL/Gmpz.h>
#include <CGAL/Homogeneous.h>
#include <CGAL/Nef_polyhedron_S2.h>

typedef CGAL::Gmpz RT;
typedef CGAL::Homogeneous<RT> Kernel;
typedef CGAL::Nef_polyhedron_S2<Kernel> Nef_polyhedron;
typedef Nef_polyhedron::Sphere_circle Sphere_circle;

int main()
{
  Nef_polyhedron N1(Sphere_circle(1,0,0));
  Nef_polyhedron N2(Sphere_circle(0,1,0), Nef_polyhedron::EXCLUDED);
  Nef_polyhedron N3 = N1 * N2;
  return 0;
}

13.3.2   Construction and Combinations

Th example shows the different types of constructors: $$N1 is the complete sphere, $$N2 is a halfsphere which includes the boundary, $$N3 is created with the copy constructor, $$N4 is created as an arrangement of a set of Sphere_segments, and $$N5 is created as the empty set.

The example also shows the use of unary set operations, binary operations, and binary predicates: $$N3 is defined as the complement of $$N2, $$N1 is compared with the union of $$N2 and $$N3, $$N5 is united with $$N2 and then intersected with $$N4. At last, it is tested if $$N5 is a subset of $$N2 and if $$N5 is not equal to $$N4.

// examples/Nef_S2/construction.C

#include <CGAL/Gmpz.h>
#include <CGAL/Homogeneous.h>
#include <CGAL/Nef_polyhedron_S2.h>

typedef CGAL::Gmpz RT;
typedef CGAL::Homogeneous<RT> Kernel;
typedef CGAL::Nef_polyhedron_S2<Kernel> Nef_polyhedron;
typedef Nef_polyhedron::Sphere_point Sphere_point;
typedef Nef_polyhedron::Sphere_segment Sphere_segment;
typedef Nef_polyhedron::Sphere_circle Sphere_circle;

int main() {

  Nef_polyhedron N1(Nef_polyhedron::COMPLETE);

  Sphere_circle c(1,1,1); // c : x + y + z = 0
  Nef_polyhedron N2(c, Nef_polyhedron::INCLUDED);
  Nef_polyhedron N3(N2.complement());
  CGAL_assertion(N1 == N2.join(N3));

  Sphere_point   p1(1,0,0), p2(0,1,0), p3(0,0,1);
  Sphere_segment s1(p1,p2), s2(p2,p3), s3(p3,p1);
  Sphere_segment triangle[3] = { s1, s2, s3 };
  Nef_polyhedron N4(triangle, triangle+3);
  Nef_polyhedron N5;
  N5 += N2;
  N5 = N5.intersection(N4);
  CGAL_assertion(N5 <= N2 && N5 != N4);

  return 0;
}

13.3.3   Exploration

By recursively composing binary and unary operations one can end with a very complex rectilinear structure. Nef_polyhedron_S2 allows read-only exploration of the structure.

In the following example, a random Nef_polyhedron_S2 S created from n halfspheres is explored. Each sface is composed of one outer sface cycles and an arbitrary number of inner sfaces cycles. The outer cycle is either an shalfloop or a cycle of shalfedges. An inner cycles additionally can be an isolated vertex. The example shows how to get the entry item it to all sface cycles of an sface sf and how to find out what type of item it is.

The macro CGAL_forall_sface_cycles_of is equivalent to a for-loop on the range [sf->sface_cycles_begin(), sf->sface_cycles_end()). An SFace_cycle_const_iterator either represents a SVertex_const_handle, a SHalfede_const_handle or a SHalfloop_const_handle. In order to find out which handle type is represented, the functions is_svertex(), is_shafledge() and is_shalfloop() are provided. Afterwards the iterator can be casted to the proper handle type.

// examples/Nef_S2/exploration.C

#include <CGAL/Gmpz.h>
#include <CGAL/Homogeneous.h>
#include <CGAL/Nef_polyhedron_S2.h>
#include <CGAL/Nef_S2/create_random_Nef_S2.h>

typedef CGAL::Gmpz RT;
typedef CGAL::Homogeneous<RT> Kernel;
typedef CGAL::Nef_polyhedron_S2<Kernel> Nef_polyhedron_S2;
typedef Nef_polyhedron_S2::SVertex_const_handle SVertex_const_handle;
typedef Nef_polyhedron_S2::SHalfedge_const_handle SHalfedge_const_handle;
typedef Nef_polyhedron_S2::SHalfloop_const_handle SHalfloop_const_handle;
typedef Nef_polyhedron_S2::SFace_const_iterator SFace_const_iterator;
typedef Nef_polyhedron_S2::SFace_cycle_const_iterator 
                           SFace_cycle_const_iterator;
			   
int main() {

  Nef_polyhedron_S2 S;
  CGAL::create_random_Nef_S2(S,5);

  int i=0;
  SFace_const_iterator sf;
  CGAL_forall_sfaces(sf,S) {
    SFace_cycle_const_iterator it;
    std::cout << "the sface cycles of sface " << i++;
    std::cout << " start with an " << std::endl; 
    CGAL_forall_sface_cycles_of(it,sf) {
      if (it.is_svertex()) {
	std::cout << "  svertex at position "; 
	std::cout << SVertex_const_handle(it)->point() << std::endl;
      }
      else if (it.is_shalfedge()) { 
	std::cout << "  shalfedge from ";
	std::cout << SHalfedge_const_handle(it)->source()->point() << " to ";
	std::cout << SHalfedge_const_handle(it)->target()->point() << std::endl;
      }
      else if (it.is_shalfloop()) {
	std::cout << "  shalfloop lying in the plane ";
	std::cout << SHalfloop_const_handle(it)->circle() << std::endl;
      }
      else
	std::cout << "something is wrong" << std::endl;
    }
  }
  return 0;
}

13.3.4   Point Location

Using the locate function, it is possible to retrive an item at a certain location on the sphere. In the following example, the item at location Sphere_point(1,0,0) in a random Nef_polyhedron_S2 is retrieved. locate returns an instance of type Object_handle, which is a container for any handle type. Here, it either a SVertex_const_handle, a SHalfedge_const_handle, a SHafloop_const_handle or a SFace_const_handle. The function CGAL::assign performs the cast operation and returns a boolean which indicates whether the cast was successful or not.

// examples/Nef_S2/point_location.C

#include <CGAL/Gmpz.h>
#include <CGAL/Homogeneous.h>
#include <CGAL/Nef_polyhedron_S2.h>
#include <CGAL/Nef_polyhedron_3.h>
#include <CGAL/Nef_S2/create_random_Nef_S2.h>

typedef CGAL::Gmpz RT;
typedef CGAL::Homogeneous<RT> Kernel;
typedef CGAL::Nef_polyhedron_S2<Kernel> Nef_polyhedron_S2;
typedef Nef_polyhedron_S2::SVertex_const_handle SVertex_const_handle;
typedef Nef_polyhedron_S2::SHalfedge_const_handle SHalfedge_const_handle;
typedef Nef_polyhedron_S2::SHalfloop_const_handle SHalfloop_const_handle;
typedef Nef_polyhedron_S2::SFace_const_handle SFace_const_handle;
typedef Nef_polyhedron_S2::Object_handle Object_handle;
typedef Nef_polyhedron_S2::Sphere_point Sphere_point;

int main() {

  Nef_polyhedron_S2 S;
  CGAL::create_random_Nef_S2(S,5);

  SVertex_const_handle sv;
  SHalfedge_const_handle se;
  SHalfloop_const_handle sl;
  SFace_const_handle sf;
  Object_handle o = S.locate(Sphere_point(1,0,0));
  if(CGAL::assign(sv,o))
    std::cout << "Locating svertex" << std::endl;
  else if(CGAL::assign(se,o))
    std::cout << "Locating shalfedge" << std::endl;
  else if(CGAL::assign(sl,o))
    std::cout << "Locating shalfloop" << std::endl;
  else if(CGAL::assign(sf,o))
    std::cout << "Locating sface" << std::endl;
  else {
    std::cout << "something wrong" << std::endl;
    return 1;
  }
  return 0;
}

13.3.5   Visualization

Nef_polyhedron_S2 provides an interface for OpenGL visualization via a Qt widget. The usage is shown in the following example:

// examples/Nef_S2/visualization.C

#ifndef CGAL_USE_QT
#include <iostream>
int main(int, char*){
  std::cout << "Sorry, this demo needs QT..." << std::endl; return 0;}
#else
#include <CGAL/Gmpz.h>
#include <CGAL/Homogeneous.h>
#include <CGAL/Nef_polyhedron_S2.h>
#include <CGAL/Nef_S2/create_random_Nef_S2.h>
#include <CGAL/IO/Qt_widget_Nef_S2.h>
#include <qapplication.h>

typedef CGAL::Gmpz RT;
typedef CGAL::Homogeneous<RT> Kernel;
typedef CGAL::Nef_polyhedron_S2<Kernel> Nef_polyhedron_S2;

int main(int argc, char* argv[]) {

  Nef_polyhedron_S2 S;
  create_random_Nef_S2(S,5);

  QApplication a(argc, argv);
  CGAL::Qt_widget_Nef_S2<Nef_polyhedron_S2>* w = 
    new CGAL::Qt_widget_Nef_S2<Nef_polyhedron_S2>(S);
  a.setMainWidget(w);
  w->show();
  return a.exec();
}
#endif

Footnotes

1	A perfect hemisphere of $$S2 is an open half-sphere plus an open half-circle in the boundary of the open half-sphere plus one endpoint of the half-circle.