TriangulationDataStructure_3

Definition

3D-triangulation data structures are meant to maintain the combinatorial information for 3D-geometric triangulations.

In CGAL, a triangulation data structure is a container of cells ($$3-faces) and vertices ($$0-faces). Each cell gives access to its four incident vertices and to its four adjacent cells. Each vertex gives direct access to one of its incident cells, which is sufficient to retrieve all the incident cells when needed.

The four vertices of a cell are indexed with 0, 1, 2 and 3. The neighbors of a cell are also indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by $$i is opposite to the vertex with the same index (see Figure ).

Edges ($$1-faces) and facets ($$2-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex of index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of indices i and j of c).

As CGAL explicitly deals with all degenerate cases, a 3D-triangulation data structure in CGAL can handle the cases when the dimension of the triangulation is lower than 3 (see Section ).

Thus, a 3D-triangulation data structure can store a triangulation of a topological sphere $$S^d of $$ ^d+1, for any $$d {-1,0,1,2,3}.

The second template parameter of the basic triangulation class (see Chapter , ) Triangulation_3 is a triangulation data structure class. (See Chapter .)

To ensure all the flexibility of the class Triangulation_3, a model of a triangulation data structure must be templated by the base vertex and the base cell classes (see ): TriangulationDataStructure_3<TriangulationVertexBase_3,TriangulationCellBase_3>. The optional functionalities related to geometry are compulsory for this use as a template parameter of Triangulation_3.

A class that satisfies the requirements for a triangulation data structure class must provide the following types and operations.

Types

TriangulationDataStructure_3::Vertex
	Vertex type
TriangulationDataStructure_3::Cell
	Cell type
TriangulationDataStructure_3::size_type
	Size type (unsigned integral type)
TriangulationDataStructure_3::difference_type
	Difference type (signed integral type)

Vertices and cells are usually manipulated via handles, which support the two dereference operators operator* and operator->.

TriangulationDataStructure_3::Vertex_handle

TriangulationDataStructure_3::Cell_handle

Requirements for Vertex and Cell are described in TriangulationDataStructure_3::Vertex and TriangulationDataStructure_3::Cell .

typedef Triple<Cell_handle, int, int>
	Edge;	(c,i,j) is the edge of cell c whose vertices indices are i and j. (See Section .)
typedef std::pair<Cell_handle, int>
	Facet;	(c,i) is the facet of c opposite to the vertex of index i. (See Section .)

The following iterators allow one to visit all the vertices, edges, facets and cells of the triangulation data structure. They are all bidirectional, non-mutable iterators.

TriangulationDataStructure_3::Cell_iterator

TriangulationDataStructure_3::Facet_iterator

TriangulationDataStructure_3::Edge_iterator

TriangulationDataStructure_3::Vertex_iterator

The following circulators allow us to visit all the cells and facets incident to a given edge. They are bidirectional and non-mutable.

TriangulationDataStructure_3::Facet_circulator

TriangulationDataStructure_3::Cell_circulator

Iterators and circulators are convertible to the corresponding handles, thus the user can pass them directly as arguments to the functions.

Creation

TriangulationDataStructure_3 tds;
	Default constructor.
TriangulationDataStructure_3 tds ( tds1);
	Copy constructor. All vertices and cells are duplicated.

TriangulationDataStructure_3&
	tds = tds1	Assignment operator. All vertices and cells are duplicated, and the former data structure of tds is deleted.
Vertex_handle	tds.copy_tds ( tds1, Vertex_handle v = Vertex_handle())
		tds1 is copied into tds. If $$v != Vertexhandle(), the vertex of tds corresponding to v is returned, otherwise Vertex_handle() is returned. Precondition: The optional argument v is a vertex of tds1.
void	tds.swap ( & tds1)
		Swaps tds and tds1. There is no copy of cells and vertices, thus this method runs in constant time. This method should be preferred to tds=tds1 or tds(tds1) when tds1 is deleted after that.
void	tds.clear ()	Deletes all cells and vertices. tds is reset as a triangulation data structure constructed by the default constructor.
void ~	tds.TriangulationDataStructure_3 ()
		Destructor. All vertices and cells are deleted, and tds itself is deleted.

Operations

Access Functions

int	tds.dimension ()	The dimension of the triangulated topological sphere.
size_type	tds.number_of_vertices ()
		The number of vertices. Note that the triangulation data structure has one more vertex than an associated geometric triangulation, if there is one, since the infinite vertex is a standard vertex and is thus also counted.
size_type	tds.number_of_cells ()
		The number of cells. Returns 0 if tds.dimension()$$<3.

Non constant-time access functions

advanced

Setting

void	tds.set_dimension ( int n)
		Sets the dimension to n.

advanced

Queries

bool	tds.is_vertex ( Vertex_handle v)
		Tests whether v is a vertex of tds.
bool	tds.is_edge ( Cell_handle c, int i, int j)
		Tests whether (c,i,j) is an edge of tds. Answers false when dimension() $$<1 . Precondition: $$i,j {0,1,2,3}
bool	tds.is_edge ( Vertex_handle u, Vertex_handle v, Cell_handle & c, int & i, int & j)
		Tests whether (u,v) is an edge of tds. If the edge is found, it computes a cell c having this edge and the indices i and j of the vertices u and v, in this order.
bool	tds.is_edge ( Vertex_handle u, Vertex_handle v)
		Tests whether (u,v) is an edge of tds.
bool	tds.is_facet ( Cell_handle c, int i)
		Tests whether (c,i) is a facet of tds. Answers false when dimension() $$<2 . Precondition: $$i {0,1,2,3}
bool	tds.is_facet ( Vertex_handle u, Vertex_handle v, Vertex_handle w, Cell_handle & c, int & i, int & j, int & k)
		Tests whether (u,v,w) is a facet of tds. If the facet is found, it computes a cell c having this facet and the indices i, j and k of the vertices u, v and w, in this order.
bool	tds.is_cell ( Cell_handle c)
		Tests whether c is a cell of tds. Answers false when dimension() $$<3 .
bool	tds.is_cell ( Vertex_handle u, Vertex_handle v, Vertex_handle w, Vertex_handle t, Cell_handle & c, int & i, int & j, int & k, int & l)
		Tests whether (u,v,w,t) is a cell of tds. If the cell c is found, it computes the indices i, j, k and l of the vertices u, v, w and t in c, in this order.

There is a method has_vertex in the cell class. The analogous methods for facets are defined here.

bool	tds.has_vertex ( Facet f, Vertex_handle v, int & j)
		If v is a vertex of f, then j is the index of v in the cell f.first, and the method returns true. Precondition: tds.dimension()=3
bool	tds.has_vertex ( Cell_handle c, int i, Vertex_handle v, int & j)
		Same for facet (c,i). Computes the index j of v in c.
bool	tds.has_vertex ( Facet f, Vertex_handle v)
bool	tds.has_vertex ( Cell_handle c, int i, Vertex_handle v)
		Same as the first two methods, but these two methods do not return the index of the vertex.

The following three methods test whether two facets have the same vertices.

bool	tds.are_equal ( Facet f, Facet g)
bool	tds.are_equal ( Cell_handle c, int i, Cell_handle n, int j)
bool	tds.are_equal ( Facet f, Cell_handle n, int j)
		For these three methods: Precondition: tds.dimension()=3.

Flips

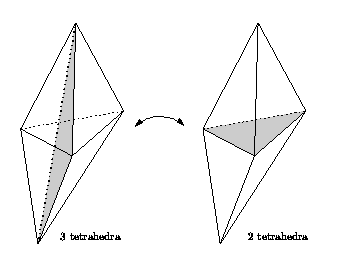
Two kinds of flips exist for a three-dimensional triangulation. They are reciprocal. To be flipped, an edge must be incident to three tetrahedra. During the flip, these three tetrahedra disappear and two tetrahedra appear. Figure (left) shows the edge that is flipped as bold dashed, and one of its three incident facets is shaded. On the right, the facet shared by the two new tetrahedra is shaded.

Figure:  Flips.

The following methods guarantee the validity of the resulting 3D combinatorial triangulation.

Flips for a 2d triangulation are not implemented yet

bool	tds.flip ( Edge e)
bool	tds.flip ( Cell_handle c, int i, int j)
		Before flipping, these methods check that edge e=(c,i,j) is flippable (which is quite expensive). They return false or true according to this test.
void	tds.flip_flippable ( Edge e)
void	tds.flip_flippable ( Cell_handle c, int i, int j)
		Should be preferred to the previous methods when the edge is known to be flippable. Precondition: The edge is flippable.
bool	tds.flip ( Facet f)
bool	tds.flip ( Cell_handle c, int i)
		Before flipping, these methods check that facet f=(c,i) is flippable (which is quite expensive). They return false or true according to this test.
void	tds.flip_flippable ( Facet f)
void	tds.flip_flippable ( Cell_handle c, int i)
		Should be preferred to the previous methods when the facet is known to be flippable. Precondition: The facet is flippable.

Insertions

The following modifier member functions guarantee the combinatorial validity of the resulting triangulation.

Vertex_handle	tds.insert_in_cell ( Cell_handle c)
		Creates a new vertex, inserts it in cell c and returns its handle. The cell c is split into four new cells, each of these cells being formed by the new vertex and a facet of c. Precondition: tds.dimension() $$= 3 and c is a cell of tds.
Vertex_handle	tds.insert_in_facet ( Facet f)
		Creates a new vertex, inserts it in facet f and returns its handle. In dimension 3, the two incident cells are split into 3 new cells; in dimension 2, the facet is split into 3 facets. Precondition: tds.dimension() $$ 2 and f is a facet of tds.
Vertex_handle	tds.insert_in_facet ( Cell_handle c, int i)
		Creates a new vertex, inserts it in facet i of c and returns its handle. Precondition: tds.dimension() $$ 2, $$i {0,1,2,3} in dimension 3, $$i=3 in dimension 2 and (c,i) is a facet of tds.
Vertex_handle	tds.insert_in_edge ( Edge e)
		Creates a new vertex, inserts it in edge e and returns its handle. In dimension 3, all the incident cells are split into 2 new cells; in dimension 2, the 2 incident facets are split into 2 new facets; in dimension 1, the edge is split into 2 new edges. Precondition: tds.dimension() $$ 1 and e is an edge of tds.
Vertex_handle	tds.insert_in_edge ( Cell_handle c, int i, int j)
		Creates a new vertex, inserts it in edge $$(i,j) of c and returns its handle. Precondition: tds.dimension() $$ 1. $$i j, $$i,j {0,1,2,3} in dimension 3, $$i,j {0,1,2} in dimension 2, $$i,j {0,1} in dimension 1 and (c,i,j) is an edge of tds.
Vertex_handle	tds.insert_increase_dimension ( Vertex_handle star = Vertex_handle())
		Transforms a triangulation of the sphere $$Sd of $$ d+1 into the triangulation of the sphere $$Sd+1 of $$ d+2 by adding a new vertex v: v is linked to all the vertices to triangulate one of the two halfspheres of dimension $$(d+1). Vertex star is used to triangulate the second halfsphere (when there is an associated geometric triangulation, star is in fact the vertex associated with its infinite vertex). See Figure . The numbering of the cells is such that, if f was a face of maximal dimension in the initial triangulation, then (f,v) (in this order) is the corresponding face in the new triangulation. This method can be used to insert the first two vertices in an empty triangulation. A handle to v is returned. Precondition: tds.dimension() $$= d < 3. When tds.number_of_vertices() $$>0, $$star Vertexhandle() and star is a vertex of tds.

Figure:  insert_increase_dimension (1-dimensional case).

template <class CellIt>
Vertex_handle	tds.insert_in_hole ( CellIt cell_begin, CellIt cell_end, Cell_handle begin, int i)
		Creates a new vertex by starring a hole. It takes an iterator range [cell_begin; cell_end[ of Cell_handles which specifies a set of connected cells (resp. facets in dimension 2) describing a hole. (begin, i) is a facet (resp. an edge) on the boundary of the hole, that is, begin belongs to the set of cells (resp. facets) previously described, and begin->neighbor(i) does not. Then this function deletes all the cells (resp. facets) describing the hole, creates a new vertex v, and for each facet (resp. edge) on the boundary of the hole, creates a new cell (resp. facet) with v as vertex. v is returned. Precondition: tds.dimension() $$ 2, the set of cells (resp. facets) is connected, and its boundary is connected.

Removal

void	tds.remove_decrease_dimension ( Vertex_handle v)
		This operation is the reciprocal of insert_increase_dimension(). It transforms a triangulation of the sphere $$Sd of $$ d+1 into the triangulation of the sphere $$Sd-1 of $$ d by removing the vertex v. Precondition: tds.dimension() $$= d -1. tds.degree(v) $$= tds.number_of_vertices() $$-1.
Cell_handle	tds.remove_from_maximal_dimension_simplex ( Vertex_handle v)
		Removes v. The incident simplices of maximal dimension incident to v are replaced by a single simplex of the same dimension. This operation is exactly the reciprocal to tds.insert_in_cell(v) in dimension 3, tds.insert_in_facet(v) in dimension 2, and tds.insert_in_edge(v) in dimension 1. Precondition: tds.degree(v) $$= tds.dimension()+1.

advanced

Other modifiers

The following modifiers can affect the validity of the triangulation data structure.

void	tds.reorient ()	Changes the orientation of all cells of the triangulation data structure. Precondition: tds.dimension() $$ 1.
Vertex_handle	tds.create_vertex ( Vertex v = Vertex())
		Adds a copy of the vertex v to the triangulation data structure.
Vertex_handle	tds.create_vertex ( Vertex_handle v)
		Creates a vertex which is a copy of the one pointed to by v and adds it to the triangulation data structure.
Cell_handle	tds.create_cell ( Cell c = Cell())
		Adds a copy of the cell c to the triangulation data structure.
Cell_handle	tds.create_cell ( Cell_handle c)
		Creates a cell which is a copy of the one pointed to by c and adds it to the triangulation data structure.
Cell_handle	tds.create_cell ( Vertex_handle v0, Vertex_handle v1, Vertex_handle v2, Vertex_handle v3)
		Creates a cell and adds it into the triangulation data structure. Initializes the vertices of the cell, its neighbor handles being initialized with the default constructed handle.
Cell_handle	tds.create_cell ( Vertex_handle v0, Vertex_handle v1, Vertex_handle v2, Vertex_handle v3, Cell_handle n0, Cell_handle n1, Cell_handle n2, Cell_handle n3)
		Creates a cell, initializes its vertices and neighbors, and adds it into the triangulation data structure.
void	tds.delete_vertex ( Vertex_handle v)
		Removes the vertex from the triangulation data structure. Precondition: The vertex is a vertex of tds.
void	tds.delete_cell ( Cell_handle c)
		Removes the cell from the triangulation data structure. Precondition: The cell is a cell of tds.
template <class VertexIt>
void	tds.delete_vertices ( VertexIt first, VertexIt last)
		Calls delete_vertex over an iterator range of value type Vertex_handle.
template <class CellIt>
void	tds.delete_cells ( CellIt first, CellIt last)
		Calls delete_cell over an iterator range of value type Cell_handle.

advanced

Traversing the triangulation

Cell_iterator	tds.cells_begin ()	Returns cells_end() when tds.dimension() $$<3.
Cell_iterator	tds.cells_end ()
Facet_iterator	tds.facets_begin ()
		Returns facets_end() when tds.dimension() $$<2.
Facet_iterator	tds.facets_end ()
Edge_iterator	tds.edges_begin ()	Returns edges_end() when tds.dimension() $$<1.
Edge_iterator	tds.edges_end ()
Vertex_iterator	tds.vertices_begin ()
Vertex_iterator	tds.vertices_end ()
Cell_circulator	tds.incident_cells ( Edge e)
		Starts at an arbitrary cell incident to e. Precondition: tds.dimension() $$=3
Cell_circulator	tds.incident_cells ( Cell_handle c, int i, int j)
		As above for edge (i,j) of c.
Cell_circulator	tds.incident_cells ( Edge e, Cell_handle start)
		Starts at cell start. Precondition: tds.dimension() $$=3 and start is incident to e.
Cell_circulator	tds.incident_cells ( Cell_handle c, int i, int j, Cell_handle start)
		As above for edge (i,j) of c.

The following circulators on facets are defined only in dimension 3, though facets are defined also in dimension 2: there are only two facets sharing an edge in dimension 2.

Facet_circulator	tds.incident_facets ( Edge e)
		Starts at an arbitrary facet incident to e. Precondition: tds.dimension() $$=3
Facet_circulator	tds.incident_facets ( Cell_handle c, int i, int j)
		As above for edge (i,j) of c.
Facet_circulator	tds.incident_facets ( Edge e, Facet start)
		Starts at facet start. Precondition: start is incident to e.
Facet_circulator	tds.incident_facets ( Edge e, Cell_handle start, int f)
		Starts at facet of index f in start.
Facet_circulator	tds.incident_facets ( Cell_handle c, int i, int j, Facet start)
		As above for edge (i,j) of c.
Facet_circulator	tds.incident_facets ( Cell_handle c, int i, int j, Cell_handle start, int f)
		As above for edge (i,j) of c and facet (start,f).

Traversal of the incident cells and the adjacent vertices of a given vertex

template <class OutputIterator>
OutputIterator	tds.incident_cells ( Vertex_handle v, OutputIterator cells)
		Copies the Cell_handles of all cells (resp. facets in dimension 2) incident to v to the output iterator cells. If tds.dimension() $$<2, then do nothing. Returns the resulting output iterator. Precondition: v $$ Vertex_handle(), tds.is_vertex(v).
template <class OutputIterator>
OutputIterator	tds.incident_vertices ( Vertex_handle v, OutputIterator vertices)
		Copies the Vertex_handles of all vertices incident to v to the output iterator vertices. If tds.dimension() $$<2, then do nothing. Returns the resulting output iterator. Precondition: v $$ Vertex_handle(), tds.is_vertex(v).
size_type	tds.degree ( Vertex_handle v)
		Returns the degree of a vertex, that is, the number of incident vertices. Precondition: v $$ Vertex_handle(), tds.is_vertex(v).

advanced

Checking

bool	tds.is_valid ( bool verbose = false)
		Checks the combinatorial validity of the triangulation by checking the validity of all its cells and vertices. (See Section .) Moreover, the Euler relation is tested. When verbose is set to true, messages are printed to give a precise indication on the kind of invalidity encountered.

advanced

I/O

istream&	istream& is >> & tds
		Reads a combinatorial triangulation from is and assigns it to tds
ostream&	ostream& os << tds
		Writes tds into the stream os

The information stored in the iostream is: the dimension, the number of vertices, the number of cells, the indices of the vertices of each cell, then the indices of the neighbors of each cell, where the index corresponds to the preceding list of cells. When dimension $$< 3, the same information is stored for faces of maximal dimension instead of cells.

Has Models

CGAL::Triangulation_data_structure_3

See Also

TriangulationDataStructure_3::Vertex
TriangulationDataStructure_3::Cell