II Geometry Kernels
|
| |
2D and 3D Linear Geometry KernelHervé Brönnimann, Andreas Fabri, Geert-Jan Giezeman, Susan Hert, Michael Hoffmann, Lutz Kettner, Sylvain Pion, and Stefan Schirra
|
 |
This package contains kernels each containing objects of
constant size, such as point, vector, direction, line, ray, segment, circle
as well as predicates and constructions for these objects. The kernels
mainly differ in the way they handle robustness issues.
|
|
Introduced in: CGAL 0.9
License: LGPL
BibTeX Key:cgal:bfghhkps-lgk23-07
Demo: Robustness
User Manual Reference Manual
|
| |
dD Geometry KernelMichael Seel
|
| |
The dD Kernel contains objects of constant size, such as point,
vector, direction, line, ray, segment, circle in d dimensional Euclidean space,
as well as predicates and constructions for these objects.
|
|
Introduced in: CGAL 1.1
License: LGPL
BibTeX Key:cgal:s-gkd-07
User Manual Reference Manual
|
| |
2D Circular Geometry Kernel Sylvain Pion and Monique Teillaud
|
 |
This package is an extension of the linear CGAL kernel. It offers
functionalities on circles, circular arcs and line segments in the
plane.
|
|
Introduced in: CGAL 3.2
License: QPL
BibTeX Key:cgal:pt-cgk2-07
Demo: Arrangement of Circular Arcs
User Manual Reference Manual
|
III Arithmetic and Algebra
|
| |
Algebraic FoundationsMichael Hemmer
|
| |
This package defines what algebra means for CGAL, in terms of
concepts, classes and functions. The main features are:
(i) explicit concepts for interoperability of types
(ii) separation between algebraic types (not necessarily embeddable
into the reals), and number types (embeddable into the reals).
|
|
Introduced in: CGAL 3.3
License: LGPL
BibTeX Key:cgal:h-ac-07
User Manual Reference Manual
|
| |
Number TypesMichael Hemmer, Susan Hert, Lutz Kettner, Sylvain Pion, and Stefan Schirra
|
| |
This package provides number type concepts as well as number type
classes and wrapper classes for third party number type libraries.
|
|
Introduced in: CGAL 1.0
License: LGPL
BibTeX Key:cgal:hhkps-nt-07
User Manual Reference Manual
|
IV Convex Hull Algorithms
|
| |
2D Convex Hulls and Extreme Points Susan Hert and Stefan Schirra
|
 |
This package provides functions
for computing convex hulls in two dimensions as well as functions for
checking if sets of points are strongly convex are not. There are also
a number of functions described for computing particular extreme
points and subsequences of hull points, such as the lower and upper
hull of a set of points.
|
|
Introduced in: CGAL 1.0
License: QPL
BibTeX Key:cgal:hs-chep2-07
Demo: 2D Convex Hull
User Manual Reference Manual
|
| |
3D Convex HullsSusan Hert and Stefan Schirra
|
 |
This package provides functions
for computing convex hulls in three dimensions as well as functions
for checking if sets of points are strongly convex or not. One can
compute the convex hull of a set of points in three dimensions in one
of three ways: using a static algorithm, using an incremental
construction algorithm, or using a triangulation to get a fully
dynamic computation.
|
|
Introduced in: CGAL 1.1
Depends on: All algorithms produce as output a 3D Polyhedron.
The dynamic algorithms depend on 3D Triangulations
License: QPL
BibTeX Key:cgal:hs-ch3-07
User Manual Reference Manual
|
| |
dD Convex Hulls and Delaunay TriangulationsSusan Hert and Michael Seel
|
| |
This package provides functions for computing convex hulls and
Delaunay triangulations in -dimensional Euclidean space.
|
|
Introduced in: CGAL 2.3
License: LGPL
BibTeX Key:cgal:hs-chdt3-07
User Manual Reference Manual
|
V Polygons and Polyhedra
|
| |
2D PolygonGeert-Jan Giezeman and Wieger Wesselink
|
 |
This package provides a polygon class and operations on
sequences of points, like the simplicity test.
|
|
Introduced in: CGAL 0.9
License: LGPL
BibTeX Key:cgal:gw-p2-07
Demo: 2D Polygon
User Manual Reference Manual
|
| |
2D Polygon Partitioning Susan Hert
|
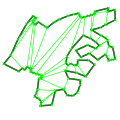 |
This package provides functions
for partitioning polygons in monotone or convex polygons.
The algorithms can produce results with the minimal number of
polygons, as well as approximations which have no more than four
times the optimal number of convex pieces but they differ in
their runtime complexities.
|
|
Introduced in: CGAL 2.3
License: QPL
BibTeX Key:cgal:h-pp2-07
Demo: 2D Polygon Partition
User Manual Reference Manual
|
| |
3D Polyhedral Surface Lutz Kettner
|
 |
Polyhedral surfaces in three dimensions are composed of
vertices, edges, facets and an incidence relationship on them. The
organization beneath is a halfedge data structure, which restricts the
class of representable surfaces to orientable 2-manifolds - with and
without boundary. If the surface is closed we call it a polyhedron.
|
|
Introduced in: CGAL 1.0
Depends on: Halfedge Data Structure
License: QPL
BibTeX Key:cgal:k-ps-07
User Manual Reference Manual
|
| |
Halfedge Data Structures Lutz Kettner
|
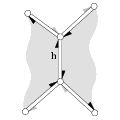 |
A halfedge data structure is an edge-centered data structure
capable of maintaining incidence information of vertices, edges and
faces, for example for planar maps, polyhedra, or other orientable,
two-dimensional surfaces embedded in arbitrary dimension. Each edge is
decomposed into two halfedges with opposite orientations. One incident
face and one incident vertex are stored in each halfedge. For each
face and each vertex, one incident halfedge is stored. Reduced
variants of the halfedge data structure can omit some of these
information, for example the halfedge pointers in faces or the
storage of faces at all.
|
|
Introduced in: CGAL 1.0
License: LGPL
BibTeX Key:cgal:k-hds-07
User Manual Reference Manual
|
VI Polygon and Polyhedron Operations
|
| |
2D Regularized Boolean Set-OperationsEfi Fogel, Ron Wein, Baruch Zukerman, and Dan Halperin
|
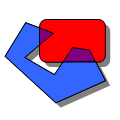 |
This package consists of the implementation of Boolean set-operations
on point sets bounded by weakly x-monotone curves in 2-dimensional
Euclidean space. In
particular, it contains the implementation of regularized Boolean
set-operations, intersection predicates, and point containment predicates.
|
|
Introduced in: CGAL 3.2
Depends on: 2D Arrangements
License: QPL
BibTeX Key:cgal:fwzh-rbso2-07
Demo: Boolean operations
User Manual Reference Manual
|
| |
2D Minkowski SumsRon Wein
|
 |
This package consists of functions that compute the Minkowski sum
of two simple straight-edge polygons in the plane. It also contains
functions for computing the Minkowski sum of a polygon and a disc,
an operation known as offsetting or dilating a polygon.
The package can compute the exact representation of the offset
polygon, or provide a guaranteed approximation of the offset.
|
|
Introduced in: CGAL 3.3
Depends on: 2D Arrangements
License: QPL
BibTeX Key:cgal:w-rms2-07
User Manual Reference Manual
|
| |
2D Boolean Operations on Nef Polygons Michael Seel
|
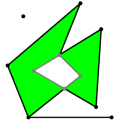 |
A Nef polygon is any set that can be obtained from a
finite set of open halfspaces by set complement and set intersection
operations. Due to the fact that all other binary set operations like
union, difference and symmetric difference can be reduced to
intersection and complement calculations, Nef polygons are also closed
under those operations. Apart from the set complement operation there
are more topological unary set operations that are closed in the
domain of Nef polygons interior, boundary, and closure.
|
|
Introduced in: CGAL 2.3
License: QPL
BibTeX Key:cgal:s-bonp2-07
Demo: 2D Nef Polygons
User Manual Reference Manual
|
| |
2D Boolean Operations on Nef Polygons Embedded on the Sphere Peter Hachenberger, Lutz Kettner, and Michael Seel
|
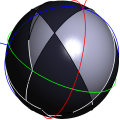 |
This package offers the equivalent to 2D Nef Polygons in the plane.
Here halfplanes correspond to half spheres delimited by great circles.
|
|
Introduced in: CGAL 3.1
Depends on: 2D Nef Polygon
BibTeX Key:cgal:hk-bonpes2-07
User Manual Reference Manual
|
| |
3D Boolean Operations on Nef PolyhedraPeter Hachenberger, Lutz Kettner, and Michael Seel
|
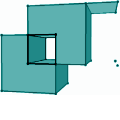 |
3D Nef polyhedra, are a
boundary representation for cell-complexes bounded by halfspaces that
supports Boolean operations and topological operations in full
generality including unbounded cells, mixed dimensional cells (e.g.,
isolated vertices and antennas). Nef polyhedra distinguish between
open and closed sets and can represent non-manifold geometry.
|
|
Introduced in: CGAL 3.1
Depends on: 2D Nef Polygons, Nef Polygons on the Sphere
License: QPL
BibTeX Key:cgal:hk-bonp3-07
User Manual Reference Manual
|
| |
2D Straight Skeleton and Polygon Offsetting Fernando Cacciola
|
 |
This package implements an algorithm to construct a halfedge data
structure representing the straight skeleton in the interior of 2D
polygons with holes and an algorithm to construct inward offset
polygons at any offset distance given a straight skeleton.
|
|
Introduced in: CGAL 3.2
Depends on: Halfedge Data Structure
License: QPL
BibTeX Key:cgal:c-sspo2-07
Demo: 2D Straight Skeleton
User Manual Reference Manual
|
VII Arrangements
|
| |
2D ArrangementRon Wein, Efi Fogel, Baruch Zukerman, and Dan Halperin
|
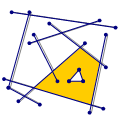 |
This package can be used to construct, maintain, alter, and display
arrangements in the plane. Once an arrangement is constructed, the
package can be used to obtain results of various queries on the
arrangement, such as point location. The package also includes generic
implementations of two algorithmic frameworks, that are, computing the
zone of an arrangement, and line-sweeping the plane, the arrangements
is embedded on. These frameworks are used in turn in the
implementations of other operations on arrangements. Computing the
overlay of two arrangements, for example, is based on the sweep-line
framework.
Arrangements and arrangement components can also be extended to store
additional data. An important extension stores the construction
history of the arrangement, such that it is possible to obtain the
originating curve of an arrangement subcurve.
|
|
Introduced in: CGAL 2.1
License: QPL
BibTeX Key:cgal:wfzh-a2-07
User Manual Reference Manual
|
| |
2D Intersection of CurvesBaruch Zukerman and Ron Wein
|
 |
This package provides three free functions implemented
based on the sweep-line paradigm: given a collection of input curves,
compute all intersection points, compute the set of subcurves that are
pairwise interior-disjoint induced by them, and check whether there
is at least one pair of curves among them that intersect in their
interior.
|
|
Introduced in: CGAL 2.4
Depends on: 2D Arrangements
License: QPL
BibTeX Key:cgal:wfz-ic2-07
User Manual Reference Manual
|
| |
2D Snap Rounding Eli Packer
|
 |
Snap Rounding is a well known method for converting
arbitrary-precision arrangements of segments into a fixed-precision
representation. In the study of robust geometric computing, it can be
classified as a finite precision approximation technique. Iterated
Snap Rounding is a modification of Snap Rounding in which each vertex
is at least half-the-width-of-a-pixel away from any non-incident
edge. This package supports both methods.
|
|
Introduced in: CGAL 3.1
Depends on: Arrangements
License: QPL
BibTeX Key:cgal:p-sr2-07
Demo: 2D Snap Rounding
User Manual Reference Manual
|
| |
2D EnvelopesRon Wein
|
 |
This package consits of functions that computes the lower (or upper)
envelope of a set of arbitrary curves in 2D. The output is
represented as an envelope diagram, namely a subdivision of the
-axis into intervals, such that the identity of the curves that
induce the envelope on each interval is unique.
|
|
Introduced in: CGAL 3.3
Depends on: 2D Arrangements
License: QPL
BibTeX Key:cgal:w-e2-07
User Manual Reference Manual
|
| |
3D EnvelopesMichal Meyerovitch, Ron Wein and Baruch Zukerman
|
 |
This package consits of functions that compute the lower (or upper)
envelope of a set of arbitrary surfaces in 3D. The output is
represented as an 2D envelope diagram, namely a planar subdivision
such that the identity of the surfaces that induce the envelope over
each diagram cell is unique.
|
|
Introduced in: CGAL 3.3
Depends on: 2D Arrangements
License: QPL
BibTeX Key:cgal:mwz-e3-07
Demo: 3D Envelopes
User Manual Reference Manual
|
VIII Triangulations and Delaunay Triangulations
|
| |
2D Triangulation Mariette Yvinec
|
 |
This package allows to build and handle
various triangulations for point sets two dimensions.
Any CGAL triangulation covers the convex hull of its
vertices. Triangulations are build incrementally
and can be modified by insertion or removal of vertices.
They offer point location facilities.
The package provides plain triangulation (whose faces
depend on the insertion order of the vertices) and
Delaunay triangulations. Regular triangulations are
also provided for sets of weighted points. Delaunay and regular
triangulations offer nearest neighbor queries
and primitives to build the dual Voronoi and power diagrams.
Finally, constrained and Delaunay constrained triangulations
allows to force some constrained segments to appear
as edges of the triangulation.
Several versions of constrained and Delaunay constrained triangulations
are provided: some of them handle intersections between input constraints
segment while others do not.
|
|
Introduced in: CGAL 0.9
Depends on: 2D Triangulation Data Structure
License: QPL
BibTeX Key:cgal:y-t2-07
Demo: Delaunay Triangulation
Demo: Regular Triangulation
Demo: Constrained Delaunay Triangulation
User Manual Reference Manual
|
| |
2D Triangulation Data Structure Sylvain Pion and Mariette Yvinec
|
| |
This package provides a data structure to store a two-dimensional
triangulation that has the topology of a two-dimensional sphere.
The package
acts as a container for the vertices and faces of the triangulation
and provides basic combinatorial operation on the triangulation.
|
|
Introduced in: CGAL 2.2
License: QPL
BibTeX Key:cgal:py-tds2-07
User Manual Reference Manual
|
| |
3D TriangulationsSylvain Pion and Monique Teillaud
|
 |
This package allows to build and handle
triangulations for point sets in three dimensions.
Any CGAL triangulation covers the convex hull of its
vertices. Triangulations are build incrementally
and can be modified by insertion or removal of vertices.
They offer point location facilities.
The package provides plain triangulation (whose faces
depends on the insertion order of the vertices) and
Delaunay triangulations. Regular triangulations are
also provided for sets of weighted points.
Delaunay and regular
triangulations offer nearest neighbor queries
and primitives to build the dual Voronoi and power diagrams.
|
|
Introduced in: CGAL 2.1
License: QPL
BibTeX Key:cgal:pt-t3-07
User Manual Reference Manual
|
| |
3D Triangulation Data Structure Sylvain Pion and Monique Teillaud
|
| |
This package provides a data structure to store a three-dimensional
triangulation that has the topology of a three-dimensional sphere.
The package acts as a container for the vertices
and cells of the triangulation
and provides basic combinatorial operations on the triangulation.
|
|
Introduced in: CGAL 2.1
License: QPL
BibTeX Key:cgal:pt-tds3-07
User Manual Reference Manual
|
| |
2D Alpha ShapesTran Kai Frank Da
|
 |
This package offers a data structure encoding the whole family of alpha-complexes
related to a given 2D Delaunay or regular triangulation. In particular, the data structure
allows to retrieve the alpha-complex for any alpha value, the whole spectrum of critical
alpha values and a filtration on the triangulation faces (this filtration is based on the first
alpha value for which each face is included on the alpha-complex).
|
|
Introduced in: CGAL 2.1
Depends on: 2D Triangulation
License: QPL
BibTeX Key:cgal:d-as2-07
Demo: 2D Alpha Shapes
User Manual Reference Manual
|
| |
3D Alpha ShapesTran Kai Frank Da and Mariette Yvinec
|
| |
This package offers a data structure encoding the whole family of alpha-complexes
related to a given 3D Delaunay or regular triangulation. In particular, the data structure
allows to retrieve the alpha-complex for any alpha value, the whole spectrum of critical
alpha values and a filtration on the triangulation faces (this filtration is based on the first
alpha value for which each face is included on the alpha-complex).
|
|
Introduced in: CGAL 2.3
Depends on: 2D Triangulation
License: QPL
BibTeX Key:cgal:dy-as3-07
User Manual Reference Manual
|
IX Voronoi Diagrams
|
| |
2D Segment Delaunay Graphs Menelaos Karavelas
|
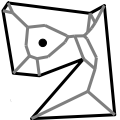 |
An algorithm for computing the dual of a Voronoi diagram of a set
of segments under the Euclidean metric. It is a generalization of the
standard Voronoi diagram for points. The algorithms provided are
dynamic.
|
|
Introduced in: CGAL 3.1
Depends on: 2D Triangulation Data Structure
License: QPL
BibTeX Key:cgal:k-sdg2-07
Demo: 2D Segment Voronoi Diagram
User Manual Reference Manual
|
| |
2D Apollonius Graphs (Delaunay Graphs of Disks)Menelaos Karavelas and Mariette Yvinec
|
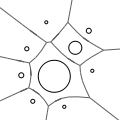 |
Algorithms for computing the Apollonius
graph in two dimensions. The Apollonius graph is the dual of the
Apollonius diagram, also known as the additively weighted Voronoi
diagram. The latter can be thought of as the Voronoi diagram of a set
of disks under the Euclidean metric, and it is a generalization of the
standard Voronoi diagram for points. The algorithms provided are
dynamic.
|
|
Introduced in: CGAL 3.0
Depends on: 2D Triangulation Data Structure
License: QPL
BibTeX Key:cgal:ky-ag2-07
Demo: 2D Apollonius Graph
User Manual Reference Manual
|
| |
2D Voronoi Diagram Adaptor Menelaos Karavelas
|
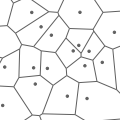 |
The 2D Voronoi diagram adaptor package provides an adaptor that adapts a
2-dimensional triangulated Delaunay graph to the corresponding
Voronoi diagram, represented as a doubly connected edge list (DCEL)
data structure. The adaptor has the ability to automatically
eliminate, in a consistent manner, degenerate features of the Voronoi
diagram, that are artifacts of the requirement that Delaunay graphs
should be triangulated even in degenerate configurations. Depending on
the type of operations that the underlying Delaunay graph supports,
the adaptor allows for the incremental or dynamic construction of
Voronoi diagrams and can support point location queries.
|
|
Introduced in: CGAL 3.2
License: QPL
BibTeX Key:cgal:k-vda2-07
User Manual Reference Manual
|
X Mesh Generation
|
| |
2D Conforming Triangulations and MeshesLaurent Rineau
|
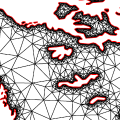 |
This package implements a Delaunay refinement algorithm to construct
conforming triangulations and 2D meshes.
Conforming Delaunay triangulations are obtained from constrained
Delaunay triangulations by refining constrained edges until they are
Delaunay edges. Conforming Gabriel triangulations are obtained by further
refining constrained edges until they become Gabriel edges.
The package provides also a 2D mesh generator that refines triangles
and constrained edges until user defined size and shape criteria on triangles
are satisfied.
The package can handle intersecting input constraints
and set no restriction on the angle formed
by two constraints sharing an endpoint.
|
|
Introduced in: CGAL 3.1
Depends on: 2D Delaunay Triangulation
License: QPL
BibTeX Key:cgal:r-ctm2-07
Demo: 2D Mesh Generator
User Manual Reference Manual
|
| |
3D Surface Mesh GenerationLaurent Rineau
and Mariette Yvinec
|
 |
This package provides functions to generate
surface meshes that interpolate
smooth surfaces. The meshing algorithm is based on Delaunay
refinement and provides some guarantees on the resulting mesh:
the user is able to control the size and shape of the mesh
elements and the accuracy of the surface approximation.
There is no restriction on the topology and number of components
of input surfaces. The surface mesh generator may also be used
for non smooth surfaces but without guarantee.
Currently, implementations
are provided for implicit surfaces described as the zero level set
of some function and surfaces described as a gray
level set in a three-dimensional image.
|
|
Introduced in: CGAL 3.2
License: QPL
BibTeX Key:cgal:ry-smg-07
User Manual Reference Manual
|
| |
3D Skin Surface Meshing Nico Kruithof
|
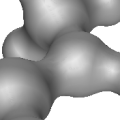 |
This package allows to build a triangular mesh of a skin surface.
Skin surfaces are used for modeling large molecules in biological
computing. The surface is defined by a set of balls, representing
the atoms of the molecule, and a shrink factor that determines the
size of the smooth patches gluing the balls together.
The construction of a triangular mesh of a smooth skin surface is
often necessary for further analysis and for fast visualization.
This package provides functions to construct a triangular mesh
approximating the skin surface from a set of balls and a shrink
factor. It also contains code to subdivide the mesh efficiently.
|
|
Introduced in: CGAL 3.3
Depends on: 3D Triangulation and 3D Polyhedral Surface
License: QPL
BibTeX Key:cgal:k-ssm3-07
User Manual Reference Manual
|
XI Geometry Processing
|
| |
3D Surface Subdivision MethodsLe-Jeng Andy Shiue
|
 |
Subdivision methods recursively refine a control mesh and generate
points approximating the limit surface. This package consists of four
popular subdivision methods and their refinement hosts. Supported
subdivision methods include Catmull-Clark, Loop, Doo-Sabin and sqrt(3)
subdivisions. Their respective refinement hosts are PQQ, PTQ, DQQ and sqrt(3) refinements. Variations of those methods
can be easily extended by substituting the geometry computation of the
refinement host.
|
|
Introduced in: CGAL 3.2
License: LGPL
BibTeX Key:cgal:s-ssm2-07
User Manual Reference Manual
|
| |
Triangulated Surface Mesh SimplificationFernando Cacciola
|
 |
This package provides an algorithm to simplify a triangulated surface mesh
by edge collapsing. It is an implementation of the Turk/Lindstrom memoryless
mesh simplification algorithm.
|
|
Introduced in: CGAL 3.3
Depends on: Polyhedron
License: QPL
BibTeX Key:cgal:c-tsms-07
User Manual Reference Manual
|
| |
Planar Parameterization of Triangulated Surface MeshesLaurent Saboret, Pierre Alliez and Bruno Lévy
|
 |
Parameterizing a surface amounts to finding a one-to-one mapping from
a suitable domain to the surface. In this package, we focus on
triangulated surfaces that are homeomorphic to a disk and on piecewise
linear mappings into a planar domain. This package implements
some of the state-of-the-art surface mesh parameterization methods,
such as least squares conformal maps, discrete conformal map, discrete
authalic parameterization, Floater mean value coordinates or Tutte
barycentric mapping.
|
|
Introduced in: CGAL 3.2
Depends on: Solvers as OpenNL or Taucs.
License: QPL
BibTeX Key:cgal:sal-pptsm2-07
User Manual Reference Manual
|
| |
2D Placement of StreamlinesAbdelkrim Mebarki
|
 |
Visualizing vector fields is important for many application domains. A
good way to do it is to generate streamlines that describe the flow
behavior. This package implements the "Farthest Point Seeding"
algorithm for placing streamlines in 2D vector fields. It generates a
list of streamlines corresponding to an input flow using a specified
separating distance. The algorithm uses a Delaunay triangulation to
model objects and address different queries, and relies on choosing the
centers of the biggest empty circles to start the integration of the
streamlines.
|
|
Introduced in: CGAL 3.2
Depends on: 2D Delaunay triangulation
License: QPL
BibTeX Key:cgal:m-ps-07
Demo: 2D Stream Lines
User Manual Reference Manual
|
| |
Approximation of Ridges and Umbilics on
Triangulated Surface Meshes Marc Pouget and Frédéric Cazals
|
 |
Global features related to curvature extrema encode
important informations used in segmentation, registration,
matching and surface analysis. Given pointwise estimations of
local differential quantities, this package allows the
approximation of differential features on a triangulated surface
mesh. Such curvature related features are curves: ridges or
crests, and points: umbilics.
|
|
Introduced in: CGAL 3.3
Depends on: Solvers as Lapack and
Blas.
License: QPL
BibTeX Key:pc-arutsm-07
User Manual Reference Manual
|
| |
Estimation of Local Differential Properties Marc Pouget and Frédéric Cazals
|
 |
For a surface discretized as a point cloud or a mesh, it
is desirable to estimate pointwise differential quantities. More
precisely, first order properties correspond to the normal or the
tangent plane; second order properties provide the principal
curvatures and directions, third order properties provide the
directional derivatives of the principal curvatures along the
curvature lines, etc. This package allows the estimation of local
differential quantities of a surface from a point sample.
|
|
Introduced in: CGAL 3.3
Depends on: Solvers as Lapack and Blas.
License: QPL
BibTeX Key:cgal:pc-eldp-07
User Manual Reference Manual
|
XII Search Structures
|
| |
2D Range and Neighbor SearchMatthias Bäsken
|
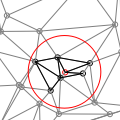 |
This package supports circular, triangular, and isorectangular range search
queries as well as (k) nearest neighbor search queries on 2D point sets.
In contrast to the spatial searching package, this package uses a
Delaunay triangulation as underlying data structure.
|
|
Introduced in: CGAL 2.1
Depends on: 2D Delaunay triangulation
License: QPL
BibTeX Key:cgal:b-ss2-07
User Manual Reference Manual
|
| |
Interval Skip ListAndreas Fabri
|
 |
An interval skip list is a data structure for finding all
intervals that contain a point, and for stabbing queries, that is for
answering the question whether a given point is contained in an
interval or not. For a triangulated terrain, this allows to quickly
identify the triangles which intersect an iso line.
|
|
Introduced in: CGAL 3.0
License: QPL
BibTeX Key:cgal:f-isl-07
User Manual Reference Manual
|
| |
dD Spatial SearchingHans Tangelder and Andreas Fabri
|
 |
This package implements exact and approximate distance browsing by
providing exact and approximate algorithms for range searching,
k-nearest and k-furthest neighbor searching, as well as incremental
nearest and incremental furthest neighbor searching, where the
query items are points in dD Euclidean space.
|
|
Introduced in: CGAL 3.0
License: QPL
BibTeX Key:cgal:tf-ssd-07
Demo: 2D Spatial Searching
User Manual Reference Manual
|
| |
dD Range and Segment Trees Gabriele Neyer
|
| |
Range and segment trees allow to perform window queries on point
sets, and to enumerate all ranges enclosing a query point. The provided data structures
are static and they are optimized for fast queries.
|
|
Introduced in: CGAL 0.9
License: QPL
BibTeX Key:cgal:n-rstd-07
User Manual Reference Manual
|
| |
Intersecting Sequences of dD Iso-oriented BoxesLutz Kettner, Andreas Meyer, and Afra Zomorodian
|
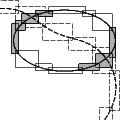 |
An efficient algorithm for finding all intersecting pairs for large
numbers of iso-oriented boxes, in order to apply a user defined callback
on them. Typically these boxes will be bounding
boxes of more complicated geometries. The algorithm is useful for (self-) intersection
tests of surfaces etc.
|
|
Introduced in: CGAL 3.1
License: QPL
BibTeX Key:cgal:kmz-isiobd-07
User Manual Reference Manual
|
XIII Shape Analysis, Fitting, and Distances
|
| |
Bounding Volumes Kaspar Fischer, Bernd Gärtner, Thomas Herrmann, Michael Hoffmann, and Sven Schönherr
|
 |
This package
provides algorithms for computing optimal bounding volumes of
point sets. In d-dimensional space, the smallest enclosing sphere,
ellipsoid (approximate), and annulus can be computed. In
3-dimensional space, the smallest enclosing strip is available as
well, and in 2-dimensional space, there are algorithms for a number
of additional volumes (rectangles, parallelograms,
axis-aligned rectangles). The smallest enclosing
sphere algorithm can also be applied to a set of
d-dimensional spheres.
|
|
Introduced in: CGAL 1.1
License: QPL
BibTeX Key:cgal:fghhs-bv-07
Demo: Smallest Enclosing Circle
Demo: Smallest Enclosing Ellipse
Demo: Smallest Enclosing Quadrilateral
Demo: 2D Rectangular p-center
User Manual Reference Manual
|
| |
Inscribed Areas Michael Hoffmann and Eli Packer
|
 |
This package provides algorithms for computing inscribed areas.
The algorithms for computing inscribed areas are: the largest inscribed
k-gon (area or perimeter) of a convex point set and the largest inscribed
iso-rectangle.
|
|
Introduced in: CGAL 1.1
License: QPL
BibTeX Key:cgal:hp-ia-07
Demo: 2D Inscribed k-gon
Demo: 2D Largest Empty Rectangle
User Manual Reference Manual
|
| |
Optimal Distances Kaspar Fischer, Bernd Gärtner, Thomas Herrmann, Michael Hoffmann, and Sven Schönherr
|
 |
This package provides algorithms for computing the distance between the
convex hulls of two point sets in d-dimensional space, without
explicitely constructing the convex hulls. It further provides
an algorithm to compute the width of a point set, and the furthest
point for each vertex of a convex polygon.
|
|
Introduced in: CGAL 1.1
License: QPL
BibTeX Key:cgal:fghhs-od-07
User Manual Reference Manual
|
| |
Principal Component AnalysisPierre Alliez and Sylvain Pion
|
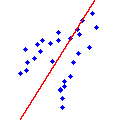 |
This package provides functions to compute global information on the
shape of a set of 2D or 3D objects such as points. It provides the
computation of axis-aligned bounding boxes, centroids of point sets,
barycenters of weighted point sets, as well as linear least squares
fitting for point sets in 2D, and point sets as well as triangle sets
in 3D.
|
|
Introduced in: CGAL 3.2
License: QPL
BibTeX Key:cgal:ap-pcad-07
Demo: 2D Least Squares Fitting
User Manual Reference Manual
|
XIV Interpolation
|
| |
2D and Surface Function InterpolationJulia Flötotto
|
| |
This package implements different methods for scattered data
interpolation: Given measures of a function on a set of discrete data
points, the task is to interpolate this function on an arbitrary query
point. The package further offers functions for natural neighbor
interpolation.
|
|
Introduced in: CGAL 3.1
License: QPL
BibTeX Key:cgal:f-i-07
User Manual Reference Manual
|
XV Kinetic Data Structures
|
| |
Kinetic Data StructuresDaniel Russel
|
 |
Kinetic data structures allow combinatorial structures
to be maintained as the primitives move. The package provides
implementations of kinetic data structures for Delaunay triangulations
in two and three dimensions, sorting of points in one dimension and
regular triangulations in three dimensions. The package supports exact
or inexact operations on primitives which move along polynomial
trajectories.
|
|
Introduced in: CGAL 3.2
Depends on: KDS Framework. Two dimensional visualization depends on Qt, three dimensional visualization depends on Coin.
License: LGPL
BibTeX Key:cgal:r-kds-07
User Manual Reference Manual
|
| |
Kinetic FrameworkDaniel Russel
|
| |
Kinetic data structures allow combinatorial geometric structures to be
maintained as the primitives move. The package provides a framework to
ease implementing and debugging kinetic data structures. The package
supports exact or inexact operations on primitives which move along
polynomial trajectories.
|
|
Introduced in: CGAL 3.2
Depends on: Two dimensional visualization depends on Qt, three dimensional visualization depends on Coin.
License: LGPL
BibTeX Key:cgal:s-kdsf-07
User Manual Reference Manual
|
XVI Support Library
|
| |
CGAL and the Boost Graph LibraryAndreas Fabri, Fernando Cacciola, and Ron Wein
|
 |
This package provides a framework for interfacing CGAL data structures with the algorithms of the BGL. It allows to run
graph algorithms directly on CGAL data structures which are
model of the BGL graph concepts, for example the shortest path
algorithm on a Delaunay triangulation in order to compute the Euclidean
minimum spanning tree.
Furthermore, it introduces a
new graph concept, the HalfedgeEdgeGraph. This concept describes
graphs which are embedded on surfaces.
|
|
Introduced in: CGAL 3.3
License: LGPL
BibTeX Key:cgal:cfw-cbgl-07
User Manual Reference Manual
|
| |
Spatial Sorting Christophe Delage
|
 |
This package provides functions
for sorting geometric objects in two and three dimensions, in order to improve
efficiency of incremental geometric algorithms.
|
|
Introduced in: CGAL 3.3
License: LGPL
BibTeX Key:cgal:d-ss-07
User Manual Reference Manual
|
| |
Monotone and Sorted Matrix Search Michael Hoffmann
|
| |
This package provides a matrix search framework, which is
the underlying technique for the computation of all furthest neighbors for the vertices of a convex polygon,
maximal k-gons inscribed into a planar point set, and computing rectangular p-centers..
|
|
Introduced in: CGAL 1.1
License: QPL
BibTeX Key:cgal:h-msms-07
User Manual Reference Manual
|
| |
Linear and Quadratic Programming Solver
Kaspar Fischer, Bernd Gärtner, Sven Schönherr, and Frans Wessendorp
|
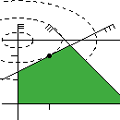 |
This package contains algorithms for minimizing linear and
convex quadratic functions over polyhedral domains, described by linear
equations and inequalities. The algorithms are exact, i.e. the solution
is computed in terms of multiprecision rational numbers.
The resulting solution is certified: along with the claims that the
problem under consideration has an optimal solution, is infeasible,
or is unbounded, the algorithms also deliver proofs for these facts.
These proofs can easily (and independently from the algorithms) be
checked for correctness.
The solution algorithms are based on a generalization of the simplex
method to quadratic objective functions.
|
|
Introduced in: CGAL 3.3
License: QPL
BibTeX Key:cgal:fgsw-lqps-07
User Manual Reference Manual
|













































