MPSFormat
MPS is a commonly used file format for storing linear and quadratic
programs according to the concepts QuadraticProgram,
LinearProgram,
NonnegativeQuadraticProgram, and
NonnegativeLinearProgram, see also
http://en.wikipedia.org/wiki/MPS_(format).
CGAL supports a large subset of
this format, but there are MPS files around that we cannot read (for
example, files that encode integrality constraints on the variables).
Also, there might be some other MPS-based solvers that will not be able
to read the MPS files written by CGAL, since we do not strictly
adhere to the very rigid layout requirements of the original MPS
format.
Let's look at an example first. The quadratic program
has the following description in MPS format.
NAME first_qp
ROWS
N obj
L c0
L c1
COLUMNS
x0 c0 1
x0 c1 -1
x1 obj -32
x1 c0 1
x1 c1 2
RHS
rhs obj -64
rhs c0 7
rhs c1 4
BOUNDS
UP BND x1 4
QMATRIX
x0 x0 2
x1 x1 8
ENDATA
Here comes a semiformal description of the format in general.
NAME section
This (mandatory) section consists of a single line
starting with NAME. Everything starting from the
first non-whitespace after that until the end of the line
constitutes the name of the problem.
ROWS section
In the (mandatory) ROW section, you find one line for every
constraint, where the letter L indicates relation 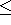 ,
letter G stands for
,
letter G stands for 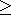 , and E for =. In
addition, there is a row for the linear objective function (indicated
by letter N). In that section, names are asigned to the
constraints (here: c0, c1) and the objective function (here:
obj). An MPS file may encode several linear objective
functions by using several rows starting with N, but we ignore
all but the first.
, and E for =. In
addition, there is a row for the linear objective function (indicated
by letter N). In that section, names are asigned to the
constraints (here: c0, c1) and the objective function (here:
obj). An MPS file may encode several linear objective
functions by using several rows starting with N, but we ignore
all but the first.
COLUMNS section
The (mandatory) COLUMNS section encodes the constraint matrix
A and the linear objective function vector c. Every line consists
of one or two sequences of three tokens j i val, where j is the
name of a variable (here, we have variables x0,x1), i is
the name of a constraint or the objective function, and val is the
value Aij (if i names a constraint), or cj (if i names the
linear objective function). Values for pairs (i,j) that are not
specified in this section default to 0. Otherwise, for every pair
(i,j), the last specified value determines Aij or cj.
RHS section
This (mandatory) section encodes the right-hand side vector b and
the constant term c0 in the objective function. The first token in
every line is an identifier (here: rhs). An MPS file may
encode several right-hand sides b by using several such identifiers,
but we ignore all lines having an identifier different from that of
the first line.
The right-hand side identifier is succeeded by one or two sequences
of tokens i val, where i names a constraint or the linear
objective function, and val specifies the value bi (if
i names a constraint), or -c0 (if i names the linear objective
function). Values that are not specified in this section default to 0.
Otherwise, for every i, the last specified value determines
bi or -c0.
BOUNDS section
This (optional) section encodes the lower and upper bound vectors l
and u for the variables. The default bounds for any variable xj are
0 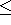 xj
xj 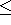
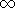 ; the
BOUNDS section is used to override these defaults. In particular,
if there is no BOUNDS section, the program is nonnegative and
actually a model of the concept NonnegativeQuadraticProgram
or NonnegativeLinearProgram.
; the
BOUNDS section is used to override these defaults. In particular,
if there is no BOUNDS section, the program is nonnegative and
actually a model of the concept NonnegativeQuadraticProgram
or NonnegativeLinearProgram.
The first token in every line is succeeded by an (optional) identifier
(here: BND). An MPS file may encode several bound vectors l
and u by using several such identifiers, but we ignore all lines
having an identifier different from that of the first line. The first
token t itself determines the type of the bound, and the token j
after the bound identifier names the variable to which the bound applies
In case of bound types FX, LO, and
UP, there is another token val that specifices the bound
value. Here is how bound type and value determine a bound for variable
xj. There may be several bound specifications for a single variable, and
they are processed in order of appearance.
|
bound type
|
resulting bound
|
|
|
FX
|
xj = val (xj becomes a fixed variable)
|
|
LO
|
xj 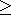 val (upper bound remains unchanged) val (upper bound remains unchanged)
|
|
UP
|
xj 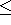 val (lower bound remains unchanged, except if val<0; then,
a zero lower bound is reset to - val (lower bound remains unchanged, except if val<0; then,
a zero lower bound is reset to - 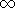 ) )
|
|
FR
|
- 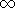 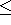 xj xj 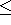 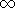 (previous bounds are discarded) (previous bounds are discarded)
|
|
MI
|
xj 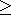 - - 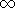 (upper bound remains unchanged) (upper bound remains unchanged)
|
|
PL
|
xj 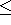 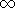 (lower bound remains unchanged) (lower bound remains unchanged)
|
QMATRIX / QUADOBJ / DMATRIX section
This (optional) section encodes the quadratic objective
function matrix D. Every line is a sequence i j val of
three tokens, where both i and j name variables, and
val is the value 2Di,j (in case of QMATRIX
or QUADOBJ), or Dij (in case of DMATRIX).
In case of QMATRIX and DMATRIX, all nonzero
entries must be specified: if there is a line i j val, then there
must also be a line j i val, since D is required to be symmetric.
In case of QUADOBJ, only the entries of 2D on or below the
diagonal must be specified, entries above the diagonal are deduced from
symmetry. It is not allowed to specify two or more different
nonzero values for an unordered pair {i,j}.
If this section is missing or does not contain nonzero values, the
program is a model of the concept LinearProgram.
Miscellaneous
Our MPS format also supports an (optional) RANGES section,
but we don't explain this here.
See Also
Quadratic_program_from_mps<NT>

