
 |
A polyhedral surface Polyhedron_3<Traits> consists of vertices , edges , facets and an incidence relation on them. Each edge is represented by two halfedges with opposite orientations.
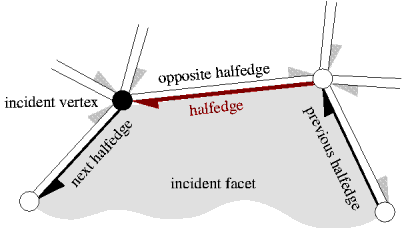
Vertices represent points in 3d-space. Edges are straight line segments between two endpoints. Facets are planar polygons without holes defined by the circular sequence of halfedges along their boundary. The polyhedral surface itself can have holes. The halfedges along the boundary of a hole are called border halfedges and have no incident facet. An edge is a border edge if one of its halfedges is a border halfedge. A surface is closed if it contains no border halfedges. A closed surface is a boundary representation for polyhedra in three dimensions. The convention is that the halfedges are oriented counterclockwise around facets as seen from the outside of the polyhedron. An implication is that the halfedges are oriented clockwise around the vertices. The notion of the solid side of a facet as defined by the halfedge orientation extends to polyhedral surfaces with border edges although they do not define a closed object. If normal vectors are considered for the facets, normals point outwards (following the right hand rule).
The strict definition can be found in [Ket99]. One implication of this definition is that the polyhedral surface is always an orientable and oriented 2-manifold with border edges, i.e., the neighborhood of each point on the polyhedral surface is either homeomorphic to a disc or to a half disc, except for vertices where many holes and surfaces with boundary can join. Another implication is that the smallest representable surface is a triangle (for polyhedral surfaces with border edges) or a tetrahedron (for polyhedra). Boundary representations of orientable 2-manifolds are closed under Euler operations. They are extended with operations that create or close holes in the surface.
Other intersections besides the incidence relation are not allowed, although they are not automatically handled, since self intersections are not easy to check efficiently. Polyhedron_3<Traits> does only maintain the combinatorial integrity of the polyhedral surface (using Euler operations) and does not consider the coordinates of the points or any geometric information.
The class Polyhedron_3<Traits> can represent polyhedral surfaces as well as polyhedra. The interface is designed in such a way that it is easy to ignore border edges and work only with polyhedra.
The sequence of edges can be ordered in the data structure on request such that the sequence starts with the non-border edges and ends with the border edges. Border edges are then itself ordered such that the halfedge which is incident to the facet comes first and the halfedge incident to the hole comes thereafter. This normalization step counts simultaneously the number of border edges. This number is zero if and only if the surface is a closed polyhedron. Note that this class does not maintain this counter nor the halfedge order during further modifications. There is no automatic caching done for auxiliary information.
#include <CGAL/Polyhedron_3.h>
The full template declaration of Polyhedron_3<Traits> states four template parameters:
| template < | class PolyhedronTraits_3, |
| class PolyhedronItems_3 = CGAL::Polyhedron_items_3, | |
| template < class T, class I> class HalfedgeDS = CGAL::HalfedgeDS_default, | |
| class Alloc = CGAL_ALLOCATOR(int)> | |
| class Polyhedron_3; |
The first parameter requires a model of the PolyhedronTraits_3 concept as argument, for example CGAL::Polyhedron_traits_3. The second parameter expects a model of the PolyhedronItems_3 concept. By default, the class CGAL::Polyhedron_items_3 is preselected. The third parameter is a class template. A model of the HalfedgeDS concept is expected. By default, the class CGAL::HalfedgeDS_default is preselected, which is a list based implementation of the halfedge data structure. The fourth parameter Alloc requires a standard allocator for STL container classes. The rebind mechanism from Alloc will be used to create appropriate allocators internally. A default is provided with the macro CGAL_ALLOCATOR(int) from the <CGAL/memory.h> header file.
|
| |
|
traits class selected for PolyhedronTraits_3.
| |
|
| |
|
items class selected for PolyhedronItems_3.
| |
|
| |
|
instantiated halfedge data structure.
| |
|
| |
|
size type of HalfedgeDS.
| |
|
| |
|
difference type of HalfedgeDS.
| |
|
| |
|
iterator category of HalfedgeDS
for all iterators.
| |
|
| |
|
circulator category of all circulators;
bidirectional category if the Items::Halfedge provides a prev()
member function, otherwise forward category.
| |
|
| |
|
allocator type Alloc.
| |
|
| |
|
vertex type.
| |
|
| |
|
halfedge type.
| |
|
| |
|
facet type.
| |
|
| |
|
point stored in vertices.
| |
|
| |
|
plane equation stored in facets (if supported).
| |
The following handles, iterators, and circulators have appropriate non-mutable counterparts, i.e., const_handle, const_iterator, and const_circulator. The mutable types are assignable to their non-mutable counterparts. Both circulators are assignable to the Halfedge_iterator. The iterators are assignable to the respective handle types. Wherever the handles appear in function parameter lists, the corresponding iterators can be used as well. For convenience, the Edge_iterator enumerates every other halfedge. It is based on the CGAL::N_step_adaptor class. For convenience, the Point_iterator enumerates all points in the polyhedral surface in the same order as the Vertex_iterator, but with the value type Point. It is based on the CGAL::Iterator_project adaptor. Similarly, a Plane_iterator is provided.

| advanced |

|
The following types are equal to either CGAL::Tag_true or CGAL::Tag_false, depending on whether the named feature is supported or not.
|
| |
|
Vertex::halfedge().
| |
|
| |
|
Vertex::point().
| |
|
| |
|
Halfedge::prev().
| |
|
| |
|
Halfedge::vertex().
| |
|
| |
|
Halfedge::facet().
| |
|
| |
|
Facet::halfedge().
| |
|
| |
|
Facet::plane().
| |
|
| |
|
supports removal of individual elements.
| |

| advanced |

|
|
| |
|
| |
|
a polyhedron P with storage reserved
for vertices, halfedges, and facets. The
reservation sizes are a hint for optimizing storage
allocation.
| |
The following Euler operations modify consistently the combinatorial structure of the polyhedral surface. The geometry remains unchanged.
|
|
| |||||
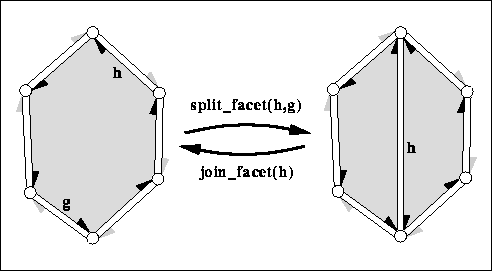
splits the facet incident to h and g into two facets
with a new diagonal between the two vertices denoted by h and
g respectively. The second (new) facet is a copy of the
first facet. Returns h->next() after the
operation, i.e., the new diagonal. The new face is to the right of the
new diagonal, the old face is to the left. The time is
proportional to the distance from h to g around the facet.
| ||||||
|
|
|
joins the two facets incident to . The facet incident to
h->opposite() gets removed. Both facets might be
holes. Returns the predecessor of around the facet. The invariant
join_facet( split_facet( h, g)) returns and keeps
the polyhedron unchanged. The time is proportional to the size of the
facet removed and the time to compute h->prev().
| ||||

|
|
| |||||
splits the vertex incident to h and g into two vertices,
the old vertex remains and a new copy is created,
and connects them with a new edge. Let hnew be
h->next()->opposite() after the split, i.e., a halfedge
of the new edge. The split regroups the halfedges around the two
vertices. The halfedge sequence hnew, g->next()->opposite(),
..., h remains around the old vertex, while the
halfedge sequence hnew->opposite(), h->next()->opposite()
(before the split), ..., g is regrouped around the new
vertex. The split returns hnew, i.e., the new halfedge incident
to the old vertex. The time is proportional to the distance from
h to g around the vertex.
| ||||||
|
|
| |||||
joins the two vertices incident to . The vertex denoted by
h->opposite() gets removed. Returns the predecessor of
around the vertex, i.e., h->opposite()->prev().
The invariant join_vertex( split_vertex( h, g)) returns
and keeps the polyhedron unchanged.
The time is proportional to the degree of the vertex removed and
the time to compute h->prev() and h->opposite()->prev().
| ||||||
|
|
| splits the halfedge h into two halfedges inserting a new vertex that is a copy of h->opposite()->vertex(). Is equivalent to split_vertex( h->prev(), h->opposite()). The call of prev() can make this method slower than a direct call of split_vertex() if the previous halfedge is already known and computing it would be costly when the halfedge data structure does not support the prev() member function. Returns the new halfedge hnew pointing to the inserted vertex. The new halfedge is followed by the old halfedge, i.e., hnew->next() == h. | ||||
|
|
|
performs an edge flip. It returns after rotating the edge one
vertex in the direction of the face orientation.
| ||||

|
|
| |||||
barycentric triangulation of h->facet(). Creates a new vertex,
a copy of h->vertex(), and connects it to each vertex incident
to h->facet() splitting h->facet() into triangles.
h remains incident to the original facet, all other triangles
are copies of this facet. Returns the halfedge h->next()
after the operation, i.e., a halfedge pointing to the new vertex.
The time is proportional to the size of the facet.
| ||||||
|
|
| |||||
reverses create_center_vertex. Erases the
vertex pointed to by g and all incident halfedges thereby
merging all incident facets. Only g->facet() remains.
The neighborhood of g->vertex() may not be triangulated,
it can have larger facets. Returns the halfedge g->prev().
Thus, the invariant h == erase_center_vertex( create_center_vertex(h)) holds if h is not a border halfedge.
The time is proportional to the sum of the size of all incident facets.
| ||||||
|
|
| |||||
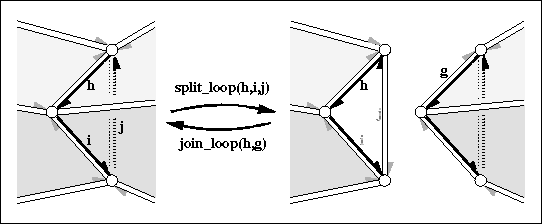
cuts the polyhedron into two parts along the cycle (edge j
runs on the backside of the three dimensional figure above).
Three new vertices (one copy for each vertex in the cycle) and three
new halfedges (one copy for each halfedge in the cycle), and two new
triangles are created. will be incident to the first new triangle.
The return value will be the halfedge incident to the second new triangle
which is the copy of h-opposite().
| ||||||
|
|
| |||||
glues the boundary of the two facets denoted by and together
and returns . Both facets and the vertices along the facet denoted
by gets removed. Both facets may be holes. The invariant
join_loop( h, split_loop( h, i, j)) returns and keeps the
polyhedron unchanged.
| ||||||
|
|
|
removes the incident facet of and changes all halfedges incident
to the facet into border edges. Returns .
See erase_facet(h) for a more generalized variant.
| ||||
|
|
|
fills a hole with a newly created facet. Makes all border halfedges
of the hole denoted by incident to the new facet. Returns .
|

|
|
| |||
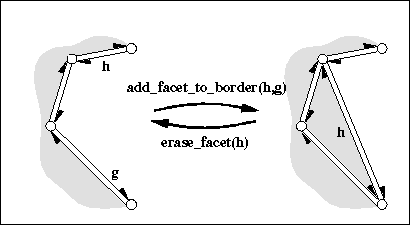
creates a new facet within the hole incident to and by
connecting the vertex denoted by with the vertex denoted by
with a new halfedge and filling this separated part of the hole with
a new facet, such that the new facet is incident to .
Returns the halfedge of the new edge that is incident to the new facet.
| ||||
|
|
| |||||
removes the incident facet of and changes all halfedges incident
to the facet into border edges or removes them from the
polyhedral surface if they were already border edges.
If this creates isolated vertices they get removed as well.
See make_hole(h) for a more specialized variant.
| ||||||
|
|
| |||||
removes the vertices, halfedges, and facets that belong to the
connected component of .
| ||||||
|
|
| removes all vertices, halfedges, and facets. | ||||

| advanced |

|
Halfedges incident to a hole are called border halfedges. An halfedge is a border edge if itself or its opposite halfedge are border halfedges. The only requirement to work with border halfedges is that the Halfedge class provides a member function is_border() returning a bool. Usually, the halfedge data structure supports facets and a NULL facet pointer will indicate a border halfedge, but this is not the only possibility. The is_border() predicate divides the edges into two classes, the border edges and the non-border edges. The following normalization reorganizes the sequential storage of the edges such that the non-border edges precede the border edges, and that for each border edge the latter one of the two halfedges is a border halfedge (the first one is a non-border halfedge in conformance with the polyhedral surface definition). The normalization stores the number of border halfedges and the halfedge iterator the border edges start at within the data structure. Halfedge insertion or removal and changing the border status of a halfedge invalidate these values. They are not automatically updated.
|
|
| sorts halfedges such that the non-border edges precede the border edges. For each border edge the halfedge iterator will reference the halfedge incident to the facet right before the halfedge incident to the hole. | ||
|
|
|
number of border halfedges.
| ||
|
|
|
number of border edges. Since each border edge of a polyhedral
surface has exactly one border halfedge,
this number is equal to size_of_border_halfedges().
| ||
|
|
|
halfedge iterator starting with the border edges. The range
[halfedges_begin(), border_halfedges_begin()) denotes
all non-border halfedges. The range
[border_halfedges_begin(), halfedges_end()) denotes all
border edges.
| ||
|
|
|
edge iterator starting with the border edges. The range
[edges_begin(), border_edges_begin()) denotes
all non-border edges. The range
[border_edges_begin(), edges_end()) denotes all
border edges.
|

| advanced |

|
|
|
| reverses facet orientations (incl. plane equations if supported). |
|
|
| |
| returns true if the polyhedral surface is combinatorially consistent. If verbose is true, statistics are printed to cerr. For level == 1 the normalization of the border edges is checked too. This method checks in particular level 3 of CGAL::Halfedge_data_structure_decorator::is_valid from page 22.5 and that each facet is at least a triangle and that the two incident facets of a non-border edge are distinct. | ||
|
|
| |
| returns true if the border halfedges are in normalized representation, which is when enumerating all halfedges with the iterator: The non-border edges precede the border edges and for border edges, the second halfedge is the border halfedge. The halfedge iterator border_halfedges_begin() denotes the first border edge. If verbose is true, statistics are printed to cerr. | ||

| advanced |

|
|
|
| |||
calls the operator() of the modifier . See
CGAL::Modifier_base for a
description of modifier design and its usage.
| ||||

| advanced |

|
CGAL::Polyhedron_3<Traits>::Vertex
CGAL::Polyhedron_3<Traits>::Halfedge
CGAL::Polyhedron_3<Traits>::Facet
PolyhedronTraits_3
CGAL::Polyhedron_traits_3<Kernel>
PolyhedronItems_3
CGAL::Polyhedron_items_3
HalfedgeDS
CGAL::HalfedgeDS_default
CGAL::Polyhedron_incremental_builder_3<HDS>
CGAL::Modifier_base.
This example program instantiates a polyhedron using the default traits class and creates a tetrahedron.
File: examples/Polyhedron/polyhedron_prog_simple.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Polyhedron_3.h>
typedef CGAL::Simple_cartesian<double> Kernel;
typedef CGAL::Polyhedron_3<Kernel> Polyhedron;
typedef Polyhedron::Halfedge_handle Halfedge_handle;
int main() {
Polyhedron P;
Halfedge_handle h = P.make_tetrahedron();
if ( P.is_tetrahedron(h))
return 0;
return 1;
}