CGAL::Triangulation_2<Traits,Tds>

Definition

The class Triangulation_2<Traits,Tds> is the basic class designed to handle triangulations of set of points $$ A in the plane.

Such a triangulation has vertices at the points of $$ A and its domain covers the convex hull of $$ A. It can be viewed as a planar partition of the plane whose bounded faces are triangular and cover the convex hull of $$ A. The single unbounded face of this partition is the complementary of the convex hull of $$ A.

In many applications, it is convenient to deal only with triangular faces. Therefore, we add to the triangulation a fictitious vertex, called the infinite vertex and we make each convex hull edge incident to an infinite face having as third vertex the infinite vertex. In that way, each edge is incident to exactly two faces and special cases at the boundary of the convex hull are simpler to deal with.

Figure 29.9:  The infinite vertex.

The class Triangulation_2<Traits,Tds> implements this point of view and therefore considers the triangulation of the set of points as a set of triangular, finite and infinite faces. Although it is convenient to draw a triangulation as in figure 29.9, note that the infinite vertex has no significant coordinates and that no geometric predicate can be applied on it or on an infinite face.

A triangulation is a collection of vertices and faces that are linked together through incidence and adjacency relations. Each face give access to its three incident vertices and to its three adjacent faces. Each vertex give access to one of its incident faces.

The three vertices of a face are indexed with 0, 1 and 2 in counterclockwise order. The neighbor of a face are also indexed with 0,1,2 in such a way that the neighbor indexed by $$i is opposite to the vertex with the same index.

The triangulation class offer two functions int cw(int i) and int ccw(int i) which given the index of a vertex in a face compute the index of the next vertex of the same face in clockwise or counterclockwise order. Thus, for example the neighbor neighbor(cw(i)) is the neighbor of f which is next to neighbor(i) turning clockwise around f. The face neighbor(cw(i)) is also the first face encountered after f when turning clockwise around vertex i of f (see Figure 29.10).

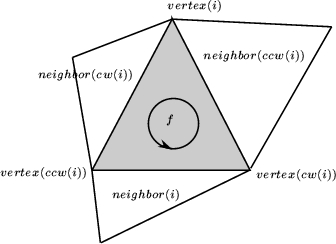
Figure 29.10:  Vertices and neighbors.

#include <CGAL/Triangulation_2.h>

Parameters

The second parameter is the triangulation data structure, it has to be instantiated by a model of the concept TriangulationDataStructure_2. By default, the triangulation data structure is instantiated by CGAL::Triangulation_data_structure_2 < CGAL::Triangulation_vertex_base_2<Gt>, CGAL::Triangulation_face_base_2<Gt> > >.

Inherits From

Types

The vertices and faces of the triangulations are accessed through handles, iterators and circulators. The handles are models of the concept Handle which basically offers the two dereference operators * and ->. The iterators and circulators are all bidirectional and non mutable. The circulators and iterators are convertible to handles with the same value type, so that whenever a handle appear in the parameter list of a function, an appropriate iterator or circulator can be passed as well.

The edges of the triangulation can also be visited through iterators and circulators, the edge circulators and iterators are also bidirectional and non mutable.

In the following, we called infinite any face or edge incident to the infinite vertex and the infinite vertex itself. Any other feature (face, edge or vertex) of the triangulation is said to be finite. Some iterators (the All iterators ) allows to visit finite or infinite feature while others (the Finite iterators) visit only finite features. Circulators visit infinite features as well as finite ones.

The triangulation class also defines the following enum type to specify which case occurs when locating a point in the triangulation.

Creation

Access Functions

advanced

Non const access

The responsibility of keeping a valid triangulation belongs to the user when using advanced operations allowing a direct manipulation of the tds.

TriangulationDataStructure_2 &

t.tds ()

Returns a reference to the triangulation data structure.

This method is mainly a help for users implementing their own triangulation algorithms.

advanced

Predicates

Queries

The class Triangulation_2<Traits,Tds> provides methods to locate a given point with respect to a triangulation. It also provides methods to locate a point with respect to a given finite face of the triangulation.

Face_handle	t.locate ( Point query, Face_handle f = Face_handle())
		If the point query lies inside the convex hull of the points, a face that contains the query in its interior or on its boundary is returned. If the point query lies outside the convex hull of the triangulation but in the affine hull, the returned face is an infinite face which is a proof of the point's location : - for a two dimensional triangulation, it is a face $$( , p, q) such that query lies to the left of the oriented line $$pq (the rest of the triangulation lying to the right of this line). - for a degenerate one dimensional triangulation it is the (degenerate one dimensional) face $$( , p, NULL) such that query and the triangulation lie on either side of p. If the point query lies outside the affine hull, the returned Face_handle is NULL. The optional Face_handle argument, if provided, is used as a hint of where the locate process has to start its search.
Face_handle	t.locate ( Point query, Locate_type& lt, int& li, Face_handle h =Face_handle())
		Same as above. Additionally, the parameters lt and li describe where the query point is located. The variable lt is set to the locate type of the query. If lt==VERTEX the variable li is set to the index of the vertex, and if lt==EDGE li is set to the index of the vertex opposite to the edge. Be careful that li has no meaning when the query type is FACE, OUTSIDE_CONVEX_HULL, or OUTSIDE_AFFINE_HULL or when the triangulation is $$0-dimensional.
Oriented_side	t.oriented_side ( Face_handle f, Point p)
		Returns on which side of the oriented boundary of f lies the point p. Precondition:  f is finite.
Oriented_side	t.side_of_oriented_circle ( Face_handle f, Point p)
		Returns on which side of the circumcircle of face f lies the point p. The circle is assumed to be counterclockwise oriented, so its positive side correspond to its bounded side. This predicate is available only if the corresponding predicates on points is provided in the geometric traits class.

Modifiers

The following operations are guaranteed to lead to a valid triangulation when they are applied on a valid triangulation.

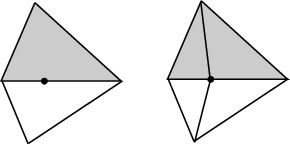
Figure 29.11:  Insertion of a point on an edge.

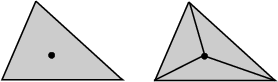
Figure 29.12:  Insertion in a face.

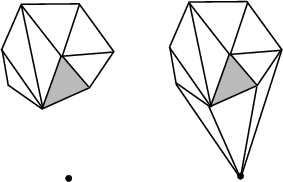
Figure 29.13:  Insertion outside the convex hull.

Figure 29.14:  Removal

advanced

The following member functions offer more specialized versions of the insertion or removal operations to be used when one knows to be in the corresponding case.

Vertex_handle	t.insert_first ( Point p)	Inserts the first finite vertex .
Vertex_handle	t.insert_second ( Point p)	Inserts the second finite vertex .
Vertex_handle	t.insert_in_face ( Point p, Face_handle f)
		Inserts vertex v in face f. Face f is modified, two new faces are created. Precondition:  The point in vertex v lies inside face f.
Vertex_handle	t.insert_in_edge ( Point p, Face_handle f, int i)
		Inserts vertex v in edge i of f. Precondition:  The point in vertex v lies on the edge opposite to the vertex i of face f.
Vertex_handle	t.insert_outside_convex_hull ( Point p, Face_handle f)
		Inserts a point which is outside the convex hull but in the affine hull. Precondition:  The handle f points to a face which is a proof of the location ofp, see the description of the locate method above.
Vertex_handle	t.insert_outside_affine_hull ( Point p)
		Inserts a point which is outside the affine hull.
void	t.remove_degree_3 ( Vertex_handle v)
		Removes a vertex of degree three. Two of the incident faces are destroyed, the third one is modified. Precondition:  Vertex v is a finite vertex with degree three.
void	t.remove_second ( Vertex_handle v)
		Removes the before last finite vertex.
void	t.remove_first ( Vertex_handle v)	Removes the last finite vertex.

The following functions are mainly intended to be used in conjunction with the find_conflicts() member functions of Delaunay and constrained Delaunay triangulations to perform insertions.

template<class EdgeIt>
Vertex_handle	t.star_hole ( Point p, EdgeIt edge_begin, EdgeIt edge_end)
		creates a new vertex v and use it to star the hole whose boundary is described by the sequence of edges [edge_begin, edge_end[. Returns a handle to the new vertex.
template<class EdgeIt, class FaceIt>
Vertex_handle	t.star_hole ( Point p, EdgeIt edge_begin, EdgeIt edge_end, FaceIt face_begin, FaceIt face_end)
		same as above, except that the algorithm first recycles faces in the sequence [face_begin, face_end[ and create new ones only when the sequence is exhausted.

advanced

Traversal of the Triangulation

A triangulation can be seen as a container of faces and vertices. Therefore the triangulation provides several iterators and circulators that allow to traverse it (completely or partially).

Face, Edge and Vertex Iterators

The following iterators allow respectively to visit finite faces, finite edges and finite vertices of the triangulation. These iterators are non mutable, bidirectional and their value types are respectively Face, Edge and Vertex. They are all invalidated by any change in the triangulation.

The following iterators allow respectively to visit all (finite or infinite) faces, edges and vertices of the triangulation. These iterators are non mutable, bidirectional and their value types are respectively Face, Edge and Vertex. They are all invalidated by any change in the triangulation.

Line Face Circulator

The triangulation defines a circulator that allows to visit all faces that are intersected by a line. A face f is considered has being intersected by the oriented line l if either:

• f is a finite face whose interior intersects l, or
• f is a finite face with an edge collinear with l and lies to the left of l, or
• f is an infinite face incident to a convex hull edge whose interior is intersected by l, or
• f is an infinite face incident to a convex hull vertex lying on l and the finite edge of f lies to the left of l.

Figure 29.15 illustrates which finite faces are enumerated. Lines $$l₁ and $$l₂ have no face to their left. Lines $$l₃ and $$l₄ have faces to their left. Note that the finite faces that are only vertex incident to lines $$l₃ and $$l₄ are not enumerated.

Figure 29.15:  The line face circulator.

A line face circulator is invalidated if the face the circulator refers to is changed.

Face, Edge and Vertex Circulators

The triangulation also provides circulators that allows to visit respectively all faces or edges incident to a given vertex or all vertices adjacent to a given vertex. These circulators are non-mutable and bidirectional. The operator++ moves the circulator counterclockwise around the vertex while the operator-- moves clockwise. A face circulator is invalidated by any modification of the face pointed to. An edge or a vertex circulator are invalidated by any modification of one of the two faces incident to the edge pointed to.

Traversal of the Convex Hull

Applied on the infinite_vertex the above functions allow to visit the vertices on the convex hull and the infinite edges and faces. Note that a counterclockwise traversal of the vertices adjacent to the infinite_vertex is a clockwise traversal of the convex hull.

Traversal between adjacent faces

Vertex_handle	t.mirror_vertex ( Face_handle f, int i)
		returns the vertex of the $$ith neighbor of f that is opposite to f. Precondition:  $$0 i 2.
int	t.mirror_index ( Face_handle f, int i)
		returns the index of f in its $$ith neighbor. Precondition:  $$0 i 2.

Miscellaneous

int	t.ccw ( int i)	Returns $$i+1 modulo 3. Precondition:  $$0 i 2.
int	t.cw ( int i)	Returns $$i+2 modulo 3. Precondition:  $$0 i 2.
Triangle	t.triangle ( Face_handle f)	Returns the triangle formed by the three vertices of f. Precondition:  The face is finite.
Segment	t.segment ( Face_handle f, int i)	Returns the line segment formed by the vertices ccw(i) and cw(i) of face f. Precondition:  $$0 i 2. The vertices ccw(i) and cw(i) of f are finite.
Segment	t.segment ( Edge e)	Returns the line segment corresponding to edge e. Precondition:  e is a finite edge
Segment	t.segment ( Edge_circulator ec)	Returns the line segment corresponding to edge *ec. Precondition:  *ec is a finite edge.
Segment	t.segment ( Edge_iterator ei)	Returns the line segment corresponding to edge *ei. Precondition:  *ei is a finite edge.
Point	t.circumcenter ( Face_handle f)	Compute the circumcenter of the face pointed to by f. This function is available only if the corresponding function is provided in the geometric traits.

advanced

Setting

void	t.set_infinite_vertex ( Vertex_handle v)

Checking

The responsibility of keeping a valid triangulation belongs to the users if advanced operations are used. Obviously the advanced user, who implements higher levels operations may have to make a triangulation invalid at some times. The following method is provided to help the debugging.

bool	t.is_valid ( bool verbose = false, int level = 0)
		Checks the combinatorial validity of the triangulation and also the validity of its geometric embedding. This method is mainly a debugging help for the users of advanced features.

advanced

I/O

The I/O operators are defined for iostream. The format for the iostream is an internal format.

The information output in the iostream is:
- the dimension, the number of vertices (including the infinite one), and the number of faces (including infinite ones).
- for each vertex (except the infinite vertex), the non combinatorial information stored in that vertex (point, etc.).
- for each faces, the indices of its vertices and the non combinatorial information (if any) in this face. - for each face again the indices of the neighboring faces.
The index of an item (vertex of face) is the rank of this item in the output order. When dimension $$< 2, the same information is output for faces of maximal dimension instead of faces.

CGAL also provides a stream operator << to draw triangulations for CGAL::Qt_widget, the Qt based graphic package. These operators require the include statement :
#include CGAL/IO/Qt_widget_Triangulation_2.h
See the Qt_widget class.

Implementation

Locate is implemented by a line walk from a vertex of the face given as optional parameter (or from a finite vertex of infinite_face() if no optional parameter is given). It takes time O(n) in the worst case, but only O(sqrt(n)) on average if the vertices are distributed uniformly at random.

Insertion of a point is done by locating a face that contains the point, and then splitting this face. If the point falls outside the convex hull, the triangulation is restored by flips. Apart from the location, insertion takes a time time O(1). This bound is only an amortized bound for points located outside the convex hull.

Removal of a vertex is done by removing all adjacent triangles, and re-triangulating the hole. Removal takes time O(d^2) in the worst case, if d is the degree of the removed vertex, which is O(1) for a random vertex.

The face, edge, and vertex iterators on finite features are derived from their counterparts visiting all (finite and infinite) features which are themselves derived from the corresponding iterators of the triangulation data structure.

See Also