
 |
#include <CGAL/polynomial_utils.h>
Given a polynomial f, or a range of values that is interpreted as the principal Sturm-Habicht coefficients of f, the function computes
| m:=# {α ∈ ℝ | f(α)=0} |
The coefficient type of the polynomial, or the value type of the iterator range, respectively must be a model of RealEmbeddable. In the second version, it is not required to pass the exact princiapl Sturm-Habicht coefficients to the functions; it is only required that the sign of each element corresponds to the sign of the actual principal Sturm-Habicht coefficient.
We explain the internals of this function. For a sequence I:=(a0, … ,an) of real numbers with a0 ≠ 0, define
| C(I)= |
| i |
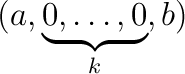
| εi:= |
|
For f ∈ ℝ[x] with deg f=n, we have:
| C(sthan(f), … ,stha0(f)) = #{α ∈ ℝ | f(α)=0} |
|
| ||
|
|
| |
| computes the number of distinct real roots of f | ||
|
| ||
|
|
| |
| computes the number of distinct real roots of f whose principal Sturm-Habicht coefficients are passed by the iterator range. | ||