31.1 Introduction
Given a set C of planar curves, the arrangement A(C) is the subdivision of the plane into zero-dimensional, one-dimensional and two-dimensional cells, called vertices, edges and faces, respectively induced by the curves in C. Arrangements are ubiquitous in the computational-geometry literature and have many applications; see, e.g., [AS00, Hal04].
The curves in C can intersect each other (a single curve may also be self-intersecting or may be comprised of several disconnected branches) and are not necessarily x-monotone.1 We construct a collection C'' of x-monotone subcurves that are pairwise disjoint in their interiors in two steps as follows. First, we decompose each curve in C into maximal x-monotone subcurves (and possibly isolated points), obtaining the collection C'. Note that an x-monotone curve cannot be self-intersecting. Then, we decompose each curve in C' into maximal connected subcurves not intersecting any other curve (or point) in C'. The collection C'' may also contain isolated points, if the curves of C contain such points. The arrangement induced by the collection C'' can be conveniently embedded as a planar graph, whose vertices are associated with curve endpoints or with isolated points, and whose edges are associated with subcurves. It is easy to see that A(C) = A(C''). This graph can be represented using a doubly-connected edge list data-structure (Dcel for short), which consists of containers of vertices, edges and faces and maintains the incidence relations among these objects.
The main idea behind the Dcel data-structure is to represent each edge using a pair of directed halfedges, one going from the xy-lexicographically smaller (left) endpoint of the curve toward its the xy-lexicographically larger (right) endpoint, and the other, known as its twin halfedge, going in the opposite direction. As each halfedge is directed, we say it has a source vertex and a target vertex. Halfedges are used to separate faces, and to connect vertices (with the exception of isolated vertices, which are unconnected).
If a vertex v is the target of a halfedge e, we say that v and e are incident to each other. The halfedges incident to a vertex v form a circular list oriented in a clockwise order around this vertex. (An isolated vertex has no incident halfedges.)
Each halfedge e stores a pointer to its incident face, which is the face lying to its left. Moreover, every halfedge is followed by another halfedge sharing the same incident face, such that the target vertex of the halfedge is the same as the source vertex of the next halfedge. The halfedges are therefore connected in circular lists, and form chains, such that all edges of a chain are incident to the same face and wind along its boundary. We call such a chain a connected component of the boundary (or CCB for short).
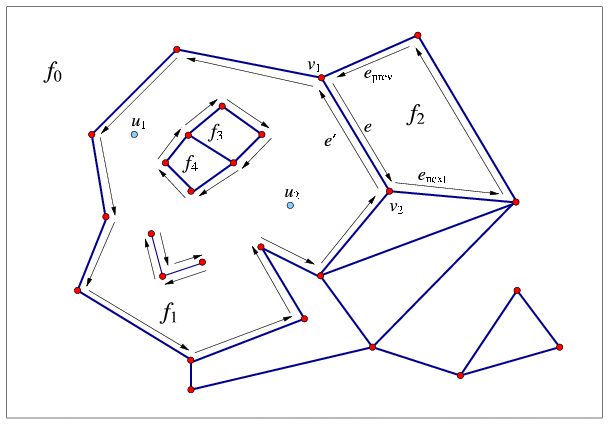
The unique CCB of halfedges winding in a counterclockwise orientation along a face boundary is referred to as the outer CCB of the face. For the time being let us consider only arrangements of bounded curves, such that exactly one unbounded face exists in every arrangement. The unbounded face does not have an outer boundary. Any other connected component of the boundary of the face is called a hole (or inner CCB), and can be represented as a circular chain of halfedges winding in a clockwise orientation around it. Note that a hole does not necessarily correspond to a single face, as it may have no area, or alternatively it may consist of several connected faces. Every face can have several holes contained in its interior (or no holes at all). In addition, every face may contain isolated vertices in its interior. See Figure 31.1 for an illustration of the various Dcel features. For more details on the Dcel data structure see [dBvKOS00, Chapter 2].
The x-monotone curves of an arrangement are embedded in an rectangular two-dimensional area called the parameter space.2 The parameter space is defined as X × Y, where X and Y are open, half-open, or closed intervals with endpoints in the compactified real line ℝ ∪ {-∞,+∞}. Let bl, br, bb, and bt denote the endpoints of X and Y, respectively. We typically refer to these values as the left, right, bottom, and top sides of the boundary of the parameter space. If the parameter space is, for example, the entire compactified plane, which is currently the only option supported by the package, bl = bb = -∞ and br = bt = +∞.
The rest of this chapter is organized as follows: In Section 31.2 we review in detail the interface of the Arrangement_2 class-template, which is the central component in the arrangement package. In Section 31.3 we show how queries on an arrangement can be issued. In Section 31.4 we review some important free (global) functions that operate on arrangements, the most important ones being the free insertion-functions. Section 31.6 contains detailed descriptions of the various geometric traits classes included in the arrangement package. Using these traits classes it is possible to construct arrangements of different families of curves. In Section 31.7 we review the notification mechanism that allows external classes to keep track of the changes that an arrangement instance goes through. Section 31.8 explains how to extend the Dcel records, to store extra data with them, and to efficiently update this data. In Section 31.9 we introduce the fundamental operation of overlaying two arrangements. Section 31.10 describes the Arrangement_with_history_2 class-template that extends the arrangement by storing additional history records with its curves. Finally, in Section 31.11 we review the arrangement input/output functions.
31.2 The Main Arrangement Class
The class Arrangement_2<Traits,Dcel> is the main class in the arrangement package. It is used to represent planar arrangements and provides the interface needed to construct them, traverse them, and maintain them. An arrangement is defined by a geometric traits class that determines the family of planar curves that form the arrangement, and a Dcel class, which represents the topological structure of the planar subdivision. It supplies a minimal set of geometric operations (predicates and constructions) required to construct and maintain the arrangement and to operate on it.
The design of the arrangement package is guided by the need to separate between the representation of the arrangements and the various geometric algorithms that operate on them, and by the need to separate between the topological and geometric aspects of the planar subdivision. The separation is exhibited by the two template parameters of the Arrangement_2 template:
- The Traits template-parameter should be instantiated with
a model of the ArrangementBasicTraits_2 concept. The traits
class defines the types of x-monotone curves and two-dimensional
points, X_monotone_curve_2 and Point_2 respectively, and
supports basic geometric predicates on them.
In the first sections of this chapter we always use Arr_segment_traits_2 as our traits class, to construct arrangements of line segments. However, the arrangement package contains several other traits classes that can handle also polylines (continuous piecewise-linear curves), conic arcs, and arcs of rational functions. We exemplify the usage of these traits classes in Section 31.6.
- The Dcel template-parameter should be instantiated with a class that is a model of the ArrangementDcel concept. The value of this parameter is Arr_default_dcel<Traits> by default. However, in many applications it is necessary to extend the Dcel features; see Section 31.8 for further explanations and examples.
31.2.1 A Simple Program
#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::Quotient<CGAL::MP_Float> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main()
{
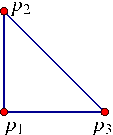
Arrangement_2 arr;
Segment_2 cv[3];
Point_2 p1 (0, 0), p2 (0, 4), p3 (4, 0);
cv[0] = Segment_2 (p1, p2);
cv[1] = Segment_2 (p2, p3);
cv[2] = Segment_2 (p3, p1);
CGAL::insert (arr, &cv[0], &cv[3]);
return (0);
}
31.2.2 Traversing the Arrangement
The simplest and most fundamental arrangement operations are the various traversal methods, which allow users to systematically go over the relevant features of the arrangement at hand.
As mentioned above, the arrangement is represented as a Dcel, which stores three containers of vertices, halfedges and faces. Thus, the Arrangement_2 class supplies iterators for these containers. For example, the methods vertices_begin() and vertices_end() return Arrangement_2::Vertex_iterator objects that define the valid range of arrangement vertices. The value type of this iterator is Arrangement_2::Vertex. Moreover, the vertex-iterator type is equivalent to Arrangement_2::Vertex_handle, which serves as a pointer to a vertex. As we show next, all functions related to arrangement features accept handle types as input parameters and return handle types as their output.
In addition to the iterators for arrangement vertices, halfedges and faces, the arrangement class also provides edges_begin() and edges_end() that return Arrangement_2::Edge_iterator objects for traversing the arrangement edges. Note that the value type of this iterator is Arrangement_2::Halfedge, representing one of the twin halfedges that represent the edge.
All iterator, circulator3 and handle types also have non-mutable (const) counterparts. These non-mutable iterators are useful to traverse an arrangement without changing it. For example, the arrangement has a non-constant member function called vertices_begin() that returns a Vertex_iterator object and another const member function that returns a Vertex_const_iterator object. In fact, all methods listed in this section that return an iterator, a circulator or a handle have non-mutable counterparts. It should be noted that, for example, Vertex_handle can be readily converted into a Vertex_const_handle, but not vice-verse.
Conversion of a non-mutable handle to a corresponding mutable handle are nevertheless possible, and can be performed using the static function Arrangement_2::non_const_handle() (see, e.g., Section 31.3.1). There are three variant of this function, one for each type of handle.
Traversal Methods for an Arrangement Vertex
A vertex is always associated with a geometric entity, namely with a Point_2 object, which can be obtained by the point() method of the Vertex class nested within Arrangement_2.
The is_isolated() method determines whether a vertex is isolated or not. Recall that the halfedges incident to a non-isolated vertex, namely the halfedges that share a common target vertex, form a circular list around this vertex. The incident_halfedges() method returns a circulator of type Arrangement_2::Halfedge_around_vertex_circulator that enables the traversal of this circular list in a clockwise direction. The value type of this circulator is Halfedge.
The following function prints all the neighbors of a given arrangement vertex (assuming that the Point_2 type can be inserted into the standard output using the << operator). The arrangement type is the same as in the simple example above.
void print_neighboring_vertices (Arrangement_2::Vertex_const_handle v)
{
if (v->is_isolated()) {
std::cout << "The vertex (" << v->point() << ") is isolated" << std::endl;
return;
}
Arrangement_2::Halfedge_around_vertex_const_circulator first, curr;
first = curr = v->incident_halfedges();
std::cout << "The neighbors of the vertex (" << v->point() << ") are:";
do {
// Note that the current halfedge is directed from u to v:
Arrangement_2::Vertex_const_handle u = curr->source();
std::cout << " (" << u->point() << ")";
} while (++curr != first);
std::cout << std::endl;
}
In case of an isolated vertex, it is possible to obtain the face that contains this vertex using the face() method.
Traversal Methods for an Arrangement Halfedge
Each arrangement edge, realized as a pair of twin halfedges, is associated with an X_monotone_curve_2 object, which can be obtained by the curve() method of the Halfedge class nested in the Arrangement_2 class.
The source() and target() methods return handles to the halfedge source and target vertices respectively. We can obtain a handle to the twin halfedge using the twin() method. From the definition of halfedges, it follows that if he is a halfedge handle, then:
- he->curve() is equivalent to he->twin()->curve(),
- he->source() is equivalent to he->twin()->target(), and
- he->target() is equivalent to he->twin()->source().
Every halfedge has an incident face that lies to its left, which can be obtained by the face() method. Recall that a halfedge is always one link in a connected chain of halfedges that share the same incident face, known as a CCB. The prev() and next() methods return handles to the previous and next halfedges in the CCB respectively.
As the CCB is a circular list of halfedges, it is only natural to traverse it using a circulator. The ccb() method returns a Arrangement_2::Ccb_halfedge_circulator object for the halfedges along the CCB.
The function print_ccb() listed below prints all x-monotone curves along a given CCB (assuming that the Point_2 and the X_monotone_curve_2 types can be inserted into the standard output using the << operator).
void print_ccb (Arrangement_2::Ccb_halfedge_const_circulator circ)
{
Ccb_halfedge_const_circulator curr = circ;
std::cout << "(" << curr->source()->point() << ")";
do {
Arrangement_2::Halfedge_const_handle he = curr->handle();
std::cout << " [" << he->curve() << "] "
<< "(" << he->target()->point() << ")";
} while (++curr != circ);
std::cout << std::endl;
}
Traversal Methods for an Arrangement Face
An arrangement of bounded curves always has a single unbounded face. The function unbounded_face() returns a handle to this face. (Note that an empty arrangement contains nothing but the unbounded face.)
Given a Face object, we can use the is_unbounded() method to determine whether it is unbounded. Bounded faces have an outer CCB, and the outer_ccb() method returns a circulator for the halfedges along this CCB. Note that the halfedges along this CCB wind in a counterclockwise orientation around the outer boundary of the face.
A face can also contain disconnected components in its interior, namely holes and isolated vertices:
- The holes_begin() and holes_end() methods return Arrangement_2::Hole_iterator iterators that define the range of holes inside the face. The value type of this iterator is Ccb_halfedge_circulator, defining the CCB that winds in a clockwise orientation around a hole.
- The isolated_vertices_begin() and isolated_vertices_end() methods return Arrangement_2::Isolated_vertex_iterator iterators that define the range of isolated vertices inside the face. The value type of this iterator is Vertex.
The function print_face() listed below prints the outer and inner boundaries of a given face, using the function print_ccb(), which was introduced in the previous subsection.
void print_face (Arrangement_2::Face_const_handle f)
{
// Print the outer boundary.
if (f->is_unbounded())
std::cout << "Unbounded face. " << std::endl;
else {
std::cout << "Outer boundary: ";
print_ccb (f->outer_ccb());
}
// Print the boundary of each of the holes.
Arrangement_2::Hole_const_iterator hi;
int index = 1;
for (hi = f->holes_begin(); hi != f->holes_end(); ++hi, ++index) {
std::cout << " Hole #" << index << ": ";
print_ccb (*hi);
}
// Print the isolated vertices.
Arrangement_2::Isolated_vertex_const_iterator iv;
for (iv = f->isolated_vertices_begin(), index = 1;
iv != f->isolated_vertices_end(); ++iv, ++index)
{
std::cout << " Isolated vertex #" << index << ": "
<< "(" << iv->point() << ")" << std::endl;
}
}
Additional Example
The function listed below prints the current setting of a given arrangement. This concludes the preview of the various traversal methods.4
void print_arrangement (const Arrangement_2& arr)
{
// Print the arrangement vertices.
Vertex_const_iterator vit;
std::cout << arr.number_of_vertices() << " vertices:" << std::endl;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
std::cout << "(" << vit->point() << ")";
if (vit->is_isolated())
std::cout << " - Isolated." << std::endl;
else
std::cout << " - degree " << vit->degree() << std::endl;
}
// Print the arrangement edges.
Edge_const_iterator eit;
std::cout << arr.number_of_edges() << " edges:" << std::endl;
for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit)
std::cout << "[" << eit->curve() << "]" << std::endl;
// Print the arrangement faces.
Face_const_iterator fit;
std::cout << arr.number_of_faces() << " faces:" << std::endl;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit)
print_face (fit);
}
31.2.3 Modifying the Arrangement
In this section we review the various member functions of the Arrangement_2 class that allow users to modify the topological structure of the arrangement by introducing new edges or vertices, modifying them, or removing them.
The arrangement member-functions that insert new curves into the arrangement, thus enabling the construction of a planar subdivision, are rather specialized, as they require a-priori knowledge on the location of the inserted curve. Indeed, for most purposes it is more convenient to construct an arrangement using the free (global) insertion-functions.
Inserting Non-Intersecting x-Monotone Curves
The most important functions that allow users to modify the arrangement, and perhaps the most frequently used ones, are the specialized insertion functions of x-monotone curves whose interior is disjoint from any other curve in the existing arrangement and do not contain any vertex of the arrangement. In addition, these function require that the location of the curve in the arrangement is known.
The motivation behind these rather harsh restrictions on the nature of the inserted curves is the decoupling of the topological arrangement representation from the various algorithms that operate on it. While the insertion of an x-monotone curve whose interior is disjoint from all existing arrangement features is quite straightforward (as we show next), inserting curves that intersect with the curves already inserted into the arrangement is much more complicated and requires the application of non-trivial geometric algorithms. These insertion operations are therefore implemented as free functions that operate on the arrangement and the inserted curve(s); see Section 31.4 for more details and examples.5
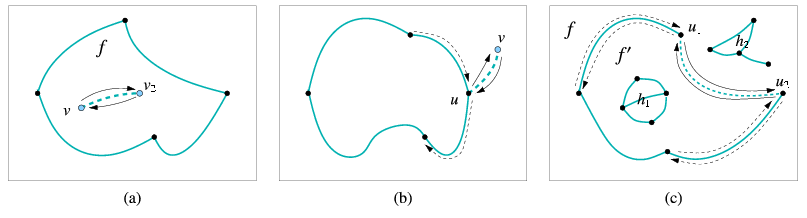
When an x-monotone curve is inserted into an existing arrangement, such that the interior of this curve is disjoint from any arrangement feature, only the following three scenarios are possible, depending on the status of the endpoints of the inserted subcurve:
- In case both curve endpoints do not correspond to any existing arrangement vertex we have to create two new vertices corresponding to the curve endpoints and connect them using a pair of twin halfedges. This halfedge pair initiates a new hole inside the face that contains the curve in its interior.
- If exactly one endpoint corresponds to an existing arrangement
vertex (we distinguish between a vertex that corresponds to the left
endpoint of the inserted curve and a vertex corresponding to its right
endpoint), we have to create a new vertex that corresponds to the other
endpoint of the curve and to connect the two vertices by a pair of
twin halfedges that form an ``antenna'' emanating from the boundary
of an existing connected component (note that if the existing vertex
used to be isolated, this operation is actually equivalent to forming
a new hole inside the face that contains this vertex).
-
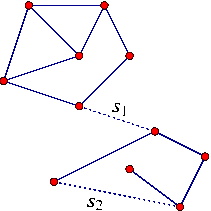
- Two disconnected components are merged into a single connected component (as is the case with the segment s1 in the figure to the left).
- A new face is created, a face that splits from an existing arrangement face. In this case we also have to examine the holes and isolated vertices in the existing face and move the relevant ones inside the new face (as is the case with the segment s2 in the figure to the left).
The Arrangement_2 class offers insertion functions named insert_in_face_interior(), insert_from_left_vertex(), insert_from_right_vertex() and insert_at_vertices() that perform the special insertion procedures listed above. The first function accepts an x-monotone curve c and an arrangement face f that contains this curve in its interior. The other functions accept an x-monotone curve c and handles to the existing vertices that correspond to the curve endpoint(s). Each of the four functions returns a handle to one of the twin halfedges that have been created, where:
- insert_in_face_interior(c, f) returns a halfedge directed from the vertex corresponding to the left endpoint of c toward the vertex corresponding to its right endpoint.
- insert_from_left_vertex(c, v) and insert_from_right_vertex(c, v) returns a halfedge whose source is the vertex v that and whose target is the new vertex that has just been created.
- insert_at_vertices(c, v1, v2) returns a halfedge directed from v1 to v2.
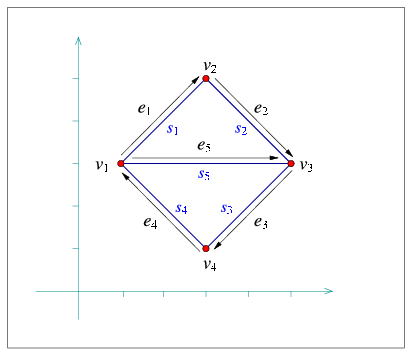
The following program demonstrates the usage of the four insertion functions. It creates an arrangement of five line segments, as depicted in Figure 31.3.6 As the arrangement is very simple, we use the simple Cartesian kernel of Cgal with integer coordinates for the segment endpoints. We also use the Arr_segment_traits_2 class that enables the efficient maintenance of arrangements of line segments; see more details on this traits class in Section 31.6. This example, as many others in this chapter, uses some print-utility functions from the file print_arr.h; these functions are also listed in Section 31.2.2.
File: examples/Arrangement_on_surface_2/edge_insertion.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include "arr_print.h"
typedef int Number_type;
typedef CGAL::Simple_cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef Arrangement_2::Vertex_handle Vertex_handle;
typedef Arrangement_2::Halfedge_handle Halfedge_handle;
int main ()
{
Arrangement_2 arr;
Segment_2 s1 (Point_2 (1, 3), Point_2 (3, 5));
Segment_2 s2 (Point_2 (3, 5), Point_2 (5, 3));
Segment_2 s3 (Point_2 (5, 3), Point_2 (3, 1));
Segment_2 s4 (Point_2 (3, 1), Point_2 (1, 3));
Segment_2 s5 (Point_2 (1, 3), Point_2 (5, 3));
Halfedge_handle e1 = arr.insert_in_face_interior (s1, arr.unbounded_face());
Vertex_handle v1 = e1->source();
Vertex_handle v2 = e1->target();
Halfedge_handle e2 = arr.insert_from_left_vertex (s2, v2);
Vertex_handle v3 = e2->target();
Halfedge_handle e3 = arr.insert_from_right_vertex (s3, v3);
Vertex_handle v4 = e3->target();
Halfedge_handle e4 = arr.insert_at_vertices (s4, v4, v1);
Halfedge_handle e5 = arr.insert_at_vertices (s5, v1, v3);
print_arrangement (arr);
return 0;
}
Observe that the first line segment is inserted in the interior of the unbounded face. The other line segments are inserted using the vertices created by the insertion of previous segments. The resulting arrangement consists of three faces, where the two bounded faces form together a hole in the unbounded face.
Manipulating Isolated Vertices
Isolated points are in general simpler geometric entities than curves and indeed the member functions that manipulate them are easier to understand.
The function insert_in_face_interior(p, f) inserts an isolated point p, located in the interior of a given face f, into the arrangement and returns a handle to the arrangement vertex it has created and associated with p. Naturally, this function has a precondition that p is really an isolated point, namely it does not coincide with any existing arrangement vertex and does not lie on any edge. As mentioned in Section 31.2.2, it is possible to obtain the face containing an isolated vertex handle v by calling v->face().
The function remove_isolated_vertex(v) receives a handle to an isolated vertex and removes it from the arrangement.
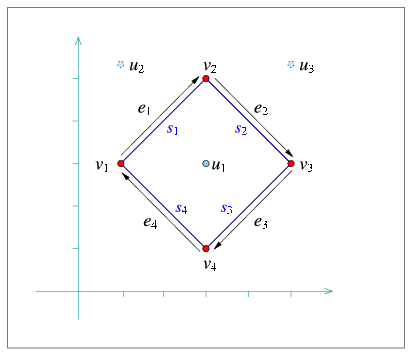
The following program demonstrates the usage of the arrangement member-functions for manipulating isolated vertices. It first inserts three isolated vertices located inside the unbounded face, then it inserts four line segments that form a rectangular hole inside the unbounded face (see Figure 31.4 for an illustration). Finally, it traverses the vertices and removes those isolated vertices that are still contained in the unbounded face (u2 and u3 in this case):
File: examples/Arrangement_on_surface_2/isolated_vertices.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include "arr_print.h"
typedef int Number_type;
typedef CGAL::Simple_cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef Arrangement_2::Vertex_handle Vertex_handle;
typedef Arrangement_2::Halfedge_handle Halfedge_handle;
typedef Arrangement_2::Face_handle Face_handle;
int main ()
{
Arrangement_2 arr;
// Insert some isolated points:
Face_handle uf = arr.unbounded_face();
Vertex_handle u1 = arr.insert_in_face_interior (Point_2 (3, 3), uf);
Vertex_handle u2 = arr.insert_in_face_interior (Point_2 (1, 5), uf);
Vertex_handle u3 = arr.insert_in_face_interior (Point_2 (5, 5), uf);
// Insert four segments that form a rectangular face:
Segment_2 s1 (Point_2 (1, 3), Point_2 (3, 5));
Segment_2 s2 (Point_2 (3, 5), Point_2 (5, 3));
Segment_2 s3 (Point_2 (5, 3), Point_2 (3, 1));
Segment_2 s4 (Point_2 (3, 1), Point_2 (1, 3));
Halfedge_handle e1 = arr.insert_in_face_interior (s1, uf);
Vertex_handle v1 = e1->source();
Vertex_handle v2 = e1->target();
Halfedge_handle e2 = arr.insert_from_left_vertex (s2, v2);
Vertex_handle v3 = e2->target();
Halfedge_handle e3 = arr.insert_from_right_vertex (s3, v3);
Vertex_handle v4 = e3->target();
Halfedge_handle e4 = arr.insert_at_vertices (s4, v4, v1);
// Remove the isolated vertices located in the unbounded face.
Arrangement_2::Vertex_iterator curr_v, next_v;
for (curr_v = arr.vertices_begin();
curr_v != arr.vertices_end(); curr_v = next_v)
{
// Store an iterator to the next vertex (as we may delete curr_v and
// invalidate the iterator).
next_v = curr_v;
++next_v;
if (curr_v->is_isolated() && curr_v->face() == uf)
arr.remove_isolated_vertex (curr_v);
}
print_arrangement (arr);
return 0;
}
Manipulating Halfedges
In the previous subsection we showed how to introduce new isolated vertices in the arrangement. But how does one create a vertex that lies on an existing arrangement edge (more precisely, on an x-monotone curve that is associated with an arrangement edge)?
It should be noted that such an operation involves the splitting of a curve at a given point in its interior, while the traits class used by Arrangement_2 does not necessarily have the ability to perform such a split operation. However, if users have the ability to split an x-monotone curve into two at a given point p (this is usually the case when employing a more sophisticated traits class; see Section 31.6 for more details) they can use the split_edge(e, c1, c2) function, were c1 and c2 are the two subcurves resulting from splitting the x-monotone curve associated with the halfedge e at some point (call it p) in its interior. The function splits the halfedge pair into two pairs, both incident to a new vertex v associated with p, and returns a handle to a halfedge whose source equals e's source vertex and whose target is the new vertex v.
The reverse operation is also possible. Suppose that we have a vertex v of degree 2, whose two incident halfedges, e1 and e2, are associated with the curves c1 and c2. Suppose further that it is possible to merge these two curves into a single continuous x-monotone curve c. Calling merge_edge(e1, e2, c) will merge the two edges into a single edge associated with the curve c, essentially removing the vertex v from the arrangement.
Finally, the function remove_edge(e) removes the edge e from the arrangement. Note that this operation is the reverse of an insertion operation, so it may cause a connected component to split into two, or two faces to merge into one, or a hole to disappear. By default, if the removal of e causes one of its end-vertices to become isolated, we remove this vertex as well. However, users can control this behavior and choose to keep the isolated vertices by supplying additional Boolean flags to remove_edge() indicating whether the source and the target vertices are to be removed should they become isolated.
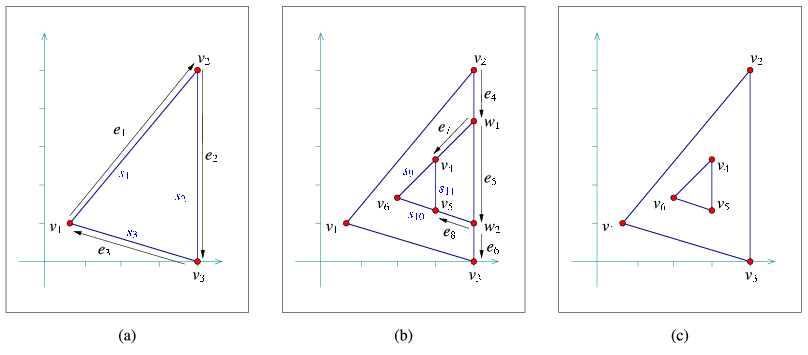
In the following example program we show how the edge-manipulation functions can be used. The program works in three steps, as demonstrated in Figure 31.5. Note that here we still stick to integer coordinates, but as we work on a larger scale we use an unbounded integer number-type (in this case, the Gmpz type taken from the Gmp library) instead of the built-in int type.7 In case the Gmp library is not installed (as indicated by the CGAL_USE_GMP flag defined in CGAL/basic.h), we use MP_Float, a number-type included in Cgal's support library that is capable of storing floating-point numbers with unbounded mantissa. We also use the standard Cartesian kernel of Cgal as our kernel. This is recommended when the kernel is instantiated with a more complex number type, as we demonstrate in other examples in this chapter.
File: examples/Arrangement_on_surface_2/edge_manipulation.cpp
#include <CGAL/basic.h>
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz Number_type;
#else
#include <CGAL/MP_Float.h>
typedef CGAL::MP_Float Number_type;
#endif
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include "arr_print.h"
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef Arrangement_2::Vertex_handle Vertex_handle;
typedef Arrangement_2::Halfedge_handle Halfedge_handle;
int main ()
{
// Step (a) - construct a triangular face.
Arrangement_2 arr;
Segment_2 s1 (Point_2 (667, 1000), Point_2 (4000, 5000));
Segment_2 s2 (Point_2 (4000, 0), Point_2 (4000, 5000));
Segment_2 s3 (Point_2 (667, 1000), Point_2 (4000, 0));
Halfedge_handle e1 = arr.insert_in_face_interior (s1, arr.unbounded_face());
Vertex_handle v1 = e1->source();
Vertex_handle v2 = e1->target();
Halfedge_handle e2 = arr.insert_from_right_vertex (s2, v2);
Vertex_handle v3 = e2->target();
Halfedge_handle e3 = arr.insert_at_vertices (s3, v3, v1);
// Step (b) - create additional two faces inside the triangle.
Point_2 p1 (4000, 3666), p2 (4000, 1000);
Segment_2 s4 (Point_2 (4000, 5000), p1);
Segment_2 s5 (p1, p2);
Segment_2 s6 (Point_2 (4000, 0), p2);
Halfedge_handle e4 = arr.split_edge(e2, s4, Segment_2 (Point_2(4000, 0), p1));
Vertex_handle w1 = e4->target();
Halfedge_handle e5 = arr.split_edge (e4->next(), s5, s6);
Vertex_handle w2 = e5->target();
Halfedge_handle e6 = e5->next();
Segment_2 s7 (p1, Point_2 (3000, 2666));
Segment_2 s8 (p2, Point_2 (3000, 1333));
Segment_2 s9 (Point_2 (3000, 2666), Point_2 (2000, 1666));
Segment_2 s10 (Point_2 (3000, 1333), Point_2 (2000, 1666));
Segment_2 s11 (Point_2 (3000, 1333), Point_2 (3000, 2666));
Halfedge_handle e7 = arr.insert_from_right_vertex (s7, w1);
Vertex_handle v4 = e7->target();
Halfedge_handle e8 = arr.insert_from_right_vertex (s8, w2);
Vertex_handle v5 = e8->target();
Vertex_handle v6 = arr.insert_in_face_interior (Point_2 (2000, 1666),
e8->face());
arr.insert_at_vertices (s9, v4, v6);
arr.insert_at_vertices (s10, v5, v6);
arr.insert_at_vertices (s11, v4, v5);
// Step (c) - remove and merge faces to form a single hole in the traingle.
arr.remove_edge (e7);
arr.remove_edge (e8);
e5 = arr.merge_edge (e5, e6, Segment_2 (e5->source()->point(),
e6->target()->point()));
e2 = arr.merge_edge (e4, e5, s2);
print_arrangement (arr);
return 0;
}
Note how we use the halfedge handles returned from split_edge() and merge_edge(). Also note the insertion of the isolated vertex v6 located inside the triangular face (the incident face of e7). This vertex seizes from being isolated, as it is gets connected to other vertices.
In this context, we should mention the two member functions modify_vertex(v, p), which sets p to be the point associated with the vertex v, and modify_edge(e, c), which sets c to be the x-monotone curve associated with the halfedge e. These functions have preconditions that p is geometrically equivalent to v->point() and c is equivalent to e->curve() (i.e., the two curves have the same graph), respectively, to avoid the invalidation of the geometric structure of the arrangement. At a first glance it may seen as these two functions are of little use. However, we should keep in mind that there may be extraneous data (probably non-geometric) associated with the point objects or with the curve objects, as defined by the traits class. With these two functions we can modify this data; see more details in Section 31.6.
In addition, we can use these functions to replace a geometric object (a point or a curve) with an equivalent object that has a more compact representation. For example, we can replace the point ((20)/(40), (99)/(33)) associated with some vertex v, by ((1)/(2), 3).
Advanced Insertion Functions
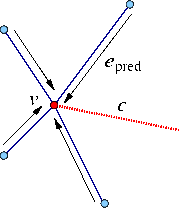
The Arrangement_2 class provides the advanced versions of the specialized insertion functions for a curve c - namely we have insert_from_left_vertex(c,pred) and insert_from_right_vertex(c,pred) that accept a halfedge pred as specified above, instead of a vertex v. These functions are more efficient, as they take constant time and do not perform any geometric operations. Thus, they should be used when the halfedge pred is known. In case that the vertex v is isolated or that the predecessor halfedge for the new inserted curve is not known, the simpler versions of these insertion functions should be used.
Similarly, there exist two overrides of the insert_at_vertices() function: One that accept the two predecessor halfedges around the two vertices v1 and v2 that correspond to the curve endpoints, and one that accepts a handle for one vertex and a predecessor halfedge around the other vertex.
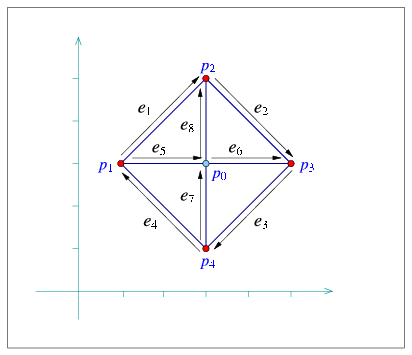
The following program shows how to construct the arrangement depicted in Figure 31.6 using the specialized insertion functions that accept predecessor halfedges:
File: examples/Arrangement_on_surface_2/special_edge_insertion.cpp
#include <CGAL/Simple_cartesian.h> #include <CGAL/Arr_segment_traits_2.h> #include <CGAL/Arrangement_2.h> #include "arr_print.h" typedef int Number_type; typedef CGAL::Simple_cartesian<Number_type> Kernel; typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2; typedef Traits_2::Point_2 Point_2; typedef Traits_2::X_monotone_curve_2 Segment_2; typedef CGAL::Arrangement_2<Traits_2> Arrangement_2; typedef Arrangement_2::Vertex_handle Vertex_handle; typedef Arrangement_2::Halfedge_handle Halfedge_handle; int main () { Arrangement_2 arr; Point_2 p0 (3, 3); Point_2 p1 (1, 3), p2 (3, 5), p3 (5, 3), p4 (3, 1); Segment_2 s1 (p1, p2); Segment_2 s2 (p2, p3); Segment_2 s3 (p3, p4); Segment_2 s4 (p4, p1); Segment_2 s5 (p1, p0); Segment_2 s6 (p0, p3); Segment_2 s7 (p4, p0); Segment_2 s8 (p0, p2); Vertex_handle v0 = arr.insert_in_face_interior (p0, arr.unbounded_face()); Halfedge_handle e1 = arr.insert_in_face_interior (s1, arr.unbounded_face()); Halfedge_handle e2 = arr.insert_from_left_vertex (s2, e1); Halfedge_handle e3 = arr.insert_from_right_vertex (s3, e2); Halfedge_handle e4 = arr.insert_at_vertices (s4, e3, e1->twin()); Halfedge_handle e5 = arr.insert_at_vertices (s5, e1->twin(), v0); Halfedge_handle e6 = arr.insert_at_vertices (s6, e5, e3->twin()); Halfedge_handle e7 = arr.insert_at_vertices (s7, e4->twin(), e6->twin()); Halfedge_handle e8 = arr.insert_at_vertices (s8, e5, e2->twin()); print_arrangement (arr); return 0; }
It is possible to perform even more refined operations on an Arrangement_2 instance given specific topological information. As most of these operations are very fragile and perform no precondition testing on their input in order to gain efficiency, they are not included in the public interface of the arrangement class. Instead, the Arr_accessor<Arrangement> class allows access to these internal arrangement operations - see more details in the Reference Manual.
31.3 Issuing Queries on an Arrangement
One of the most important query types defined on arrangements is the point-location query: Given a point, find the arrangement cell that contains it. Typically, the result of a point-location query is one of the arrangement faces, but in degenerate situations the query point can be located on an edge or coincide with a vertex.
Point-location queries are not only common in many applications, they also play an important role in the free insertion-functions (see Section 31.4). Therefore, it is crucial to have the ability to answer such queries effectively for any arrangement instance.
31.3.1 Point-Location Queries
The arrangement package includes several classes (more precisely, class templates parameterized by an arrangement class) that model the ArrangementPointLocation_2 concept. Namely, they all have a member function called locate(q) that accepts a query point q and result with a Cgal Object that wraps a handle to the arrangement cell containing the query point. This object can be assigned to either a Face_const_handle, Halfedge_const_handle or a Vertex_const_handle, depending on whether the query point is located inside a face, on an edge or on a vertex.
Note that the handles returned by the locate() functions are const (non-mutable) handles. If necessary, such handles may be casted to mutable handles using the static functions Arrangement_on_surface_2::non_const_handle() provided by the arrangement class.
An instance of any point-location class must be attached to an Arrangement_on_surface_2 instance so we can use it to issue point-location queries. This attachment can be performed when the point-location instance is constructed, or at a later time, using the init(arr) method, where arr is the attached Arrangement_on_surface_2 instance. In this chapter we always use the first option.
The following function template, which can be found in the example file point_location_utils.h, accepts a point-location object (whose type can be any of the models to the ArrangementPointLocation_2 concept) and a query point, and prints out the result of the point-location query for the given point. Observe how we use the function CGAL::assign() is order to cast the resulting CGAL::Object into a handle to an arrangement feature. The point-location object pl is assumed to be already associated with an arrangement:
template <class PointLocation>
void point_location_query
(const PointLocation& pl,
const typename PointLocation::Arrangement_on_surface_2::Point_2& q)
{
// Perform the point-location query.
CGAL::Object obj = pl.locate (q);
// Print the result.
typedef typename PointLocation::Arrangement_on_surface_2 Arrangement_on_surface_2;
typename Arrangement_on_surface_2::Vertex_const_handle v;
typename Arrangement_on_surface_2::Halfedge_const_handle e;
typename Arrangement_on_surface_2::Face_const_handle f;
std::cout << "The point " << q << " is located ";
if (CGAL::assign (f, obj)) {
// q is located inside a face:
if (f->is_unbounded())
std::cout << "inside the unbounded face." << std::endl;
else
std::cout << "inside a bounded face." << std::endl;
}
else if (CGAL::assign (e, obj)) {
// q is located on an edge:
std::cout << "on an edge: " << e->curve() << std::endl;
}
else if (CGAL::assign (v, obj)) {
// q is located on a vertex:
if (v->is_isolated())
std::cout << "on an isolated vertex: " << v->point() << std::endl;
else
std::cout << "on a vertex: " << v->point() << std::endl;
}
else {
CGAL_assertion_msg (false, "Invalid object.");
}
}
Choosing a Point-Location Strategy
Each of the various point-location classes employs a different algorithm or strategy8 for answering queries:
- Arr_naive_point_location<Arrangement> locates the query point naively, by exhaustively scanning all arrangement cells.
- Arr_walk_along_a_line_point_location<Arrangement> simulates a traversal, in reverse order, along an imaginary vertical ray emanating from the query point: It starts from the unbounded face of the arrangement and moves downward toward the query point until locating the arrangement cell containing it.
- Arr_landmarks_point_location<Arrangement,Generator>
uses a set of ``landmark'' points whose location in the
arrangement is known. Given a query point, it uses a Kd-tree to
find the nearest landmark and then traverses the straight line
segment connecting this landmark to the query point.
There are various ways to select the landmark set in the arrangement, determined by the Generator template parameter. By default, the generator class Arr_landmarks_vertices_generator is used and the arrangement vertices are the selected landmarks, but other landmark generators, such as sampling random points or choosing points on a grid, are also available; see the Reference Manual for more details.
- Arr_trapezoid_ric_point_location<Arrangement> implements Mulmuley's point-location algorithm [Mul90] (see also [dBvKOS00, Chapter 6]). The arrangement faces are decomposed into simpler cells of constant complexity known as pseudo-trapezoids and a search-structure (a directed acyclic graph) is constructed on top of these cells, allowing to locate the pseudo-trapezoid (hence the arrangement cell) containing a query point in expected logarithmic time.
The main advantage of the first two strategies is that they do not require any extra data, so the respective classes just store a pointer to an arrangement object and operate directly on it. Attaching such point-location objects to an existing arrangement has virtually no running-time cost at all, but the query time is linear in the size of the arrangement (the performance of the ``walk'' strategy is much better in practice, but its worst-case performance is linear). Using these strategies is therefore recommended only when a relatively small number of point-location queries are issued by the application, or when the arrangement is constantly changing (i.e., changes in the arrangement structure are more frequent than point-location queries).
On the other hand, the landmarks and the trapezoid RIC strategies require auxiliary data structures on top of the arrangement, which they need to construct once they are attached to an arrangement object and need to keep up-to-date as this arrangement changes. The data structures needed by both strategies can be constructed in O(N log N) time (where N is the overall number of edges in the arrangement), but the construction needed by the landmark algorithm is in practice significantly faster. In addition, although both resulting data structures are asymptotically linear in size, the Kd-tree that the landmark algorithm stores needs significantly less memory. We note that Mulmuley's algorithm guarantees a logarithmic query time, while the query time for the landmark strategy is only logarithmic on average - and we may have scenarios where the query time can be linear. In practice however, the query times of both strategies are competitive. For a detailed experimental comparison, see [HH05]
The main drawback in the current implementation of the landmark strategy, compared to the trapezoidal RIC strategy, is that while the updating the auxiliary data structures related to the trapezoidal decomposition is done very efficiently, the Kd-tree maintained by the landmark algorithm needs to be frequently rebuilt as the arrangement changes. In addition, using the landmark point-location class adds some extra requirement from the traits class (that is, the traits class should be a model of a refined concept ArrangementLandmarkTraits_2; see Section 31.6 for the details). However, most built-in traits classes that come with the Cgal public release support these extra operations.
It is therefore recommended to use the Arr_landmarks_point_location class when the application frequently issues point-location queries on an arrangement that only seldom changes. If the arrangement is more dynamic and is frequently going through changes, the Arr_trapezoid_ric_point_location class should be the selected point-location strategy.
An Example
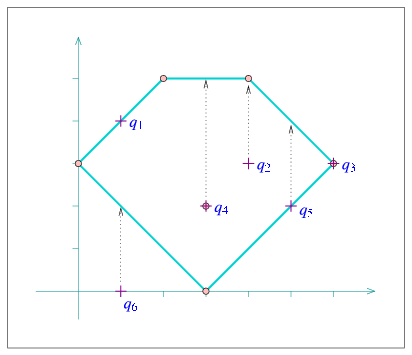
The following program constructs a simple arrangement of five line segments that form a pentagonal face, with a single isolated vertex in its interior, as depicted in Figure 31.7 (the arrangement construction is performed by the function construct_segment_arr() whose listing is omitted here and can be found in point_location_utils.h). It then employs the naive and the landmark strategies to issue several point-location queries on this arrangement:
File: examples/Arrangement_on_surface_2/point_location.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_naive_point_location.h>
#include <CGAL/Arr_landmarks_point_location.h>
#include "point_location_utils.h"
typedef int Number_type;
typedef CGAL::Simple_cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_naive_point_location<Arrangement_2> Naive_pl;
typedef CGAL::Arr_landmarks_point_location<Arrangement_2> Landmarks_pl;
int main ()
{
// Construct the arrangement.
Arrangement_2 arr;
Naive_pl naive_pl (arr);
Landmarks_pl landmarks_pl;
construct_segments_arr (arr);
// Perform some point-location queries using the naive strategy.
Point_2 q1 (1, 4);
Point_2 q2 (4, 3);
Point_2 q3 (6, 3);
point_location_query (naive_pl, q1);
point_location_query (naive_pl, q2);
point_location_query (naive_pl, q3);
// Attach the landmarks object to the arrangement and perform queries.
Point_2 q4 (3, 2);
Point_2 q5 (5, 2);
Point_2 q6 (1, 0);
landmarks_pl.attach (arr);
point_location_query (landmarks_pl, q4);
point_location_query (landmarks_pl, q5);
point_location_query (landmarks_pl, q6);
return 0;
}
Note that the program uses the auxiliary point_location_query() function template to nicely print the result of each query. This function can be found in the header file point_location_utils.h.
31.3.2 Vertical Ray Shooting
Another important query issued on arrangements is the vertical ray-shooting query: Given a query point, which arrangement feature do we encounter if we shoot a vertical ray emanating upward (or downward) from this point? In the general case the ray hits an edge, but it is possible that it hits a vertex, or that the arrangement does not have any feature lying directly above (or below) the query point.
All point-location classes listed in the previous section are also models of the ArrangementVerticalRayShoot_2 concept. That is, they all have member functions called ray_shoot_up(q) and ray_shoot_down(q) that accept a query point q and output a Cgal Object. This can be assigned to either a Halfedge_const_handle or to a Vertex_const_handle. Alternatively, the returned value is a Face_const_handle for the unbounded face of the arrangement, in case there is no edge or vertex lying directly above (or below) q.
The following function template, vertical_ray_shooting_query(), which also located in the header file point_location_utils.h, accepts a vertical ray-shooting object, whose type can be any of the models to the ArrangementVerticalRayShoot_2 concept and prints out the result of the upward vertical ray-shooting operations from a given query point. The ray-shooting object vrs is assumed to be already associated with an arrangement:
template <class VerticalRayShoot>
void vertical_ray_shooting_query
(const VerticalRayShoot& vrs,
const typename VerticalRayShoot::Arrangement_on_surface_2::Point_2& q)
{
// Perform the point-location query.
CGAL::Object obj = vrs.ray_shoot_up (q);
// Print the result.
typedef typename VerticalRayShoot::Arrangement_on_surface_2 Arrangement_on_surface_2;
typename Arrangement_on_surface_2::Vertex_const_handle v;
typename Arrangement_on_surface_2::Halfedge_const_handle e;
typename Arrangement_on_surface_2::Face_const_handle f;
std::cout << "Shooting up from " << q << " : ";
if (CGAL::assign (e, obj)) {
// We hit an edge:
std::cout << "hit an edge: " << e->curve() << std::endl;
}
else if (CGAL::assign (v, obj)) {
// We hit a vertex:
if (v->is_isolated())
std::cout << "hit an isolated vertex: " << v->point() << std::endl;
else
std::cout << "hit a vertex: " << v->point() << std::endl;
}
else if (CGAL::assign (f, obj)) {
// We did not hit anything:
CGAL_assertion (f->is_unbounded());
std::cout << "hit nothing." << std::endl;
}
else {
CGAL_assertion_msg (false, "Invalid object.");
}
}
The following program uses the auxiliary function listed above to perform vertical ray-shooting queries on an arrangement. The arrangement and the query points are exactly the same as in point_location.cpp (see Figure 31.7):
File: examples/Arrangement_on_surface_2/vertical_ray_shooting.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_walk_along_line_point_location.h>
#include <CGAL/Arr_trapezoid_ric_point_location.h>
#include "point_location_utils.h"
typedef CGAL::MP_Float Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_walk_along_line_point_location<Arrangement_2> Walk_pl;
typedef CGAL::Arr_trapezoid_ric_point_location<Arrangement_2> Trap_pl;
int main ()
{
// Construct the arrangement.
Arrangement_2 arr;
Walk_pl walk_pl (arr);
Trap_pl trap_pl;
construct_segments_arr (arr);
// Perform some vertical ray-shooting queries using the walk strategy.
Point_2 q1 (1, 4);
Point_2 q2 (4, 3);
Point_2 q3 (6, 3);
vertical_ray_shooting_query (walk_pl, q1);
vertical_ray_shooting_query (walk_pl, q2);
vertical_ray_shooting_query (walk_pl, q3);
// Attach the trapezoid-RIC object to the arrangement and perform queries.
Point_2 q4 (3, 2);
Point_2 q5 (5, 2);
Point_2 q6 (1, 0);
trap_pl.attach (arr);
vertical_ray_shooting_query (trap_pl, q4);
vertical_ray_shooting_query (trap_pl, q5);
vertical_ray_shooting_query (trap_pl, q6);
return 0;
}
The number type we use in this example is Cgal's built-in MP_Float type which is a floating-point number with an unbounded mantissa and a 32-bit exponent. It supports construction from an integer or from a machine float or double and performs additions, subtractions and multiplications in an exact number.
31.3.3 Batched Point-Location
Suppose that at a given moment our application has to issue a relatively large number m of point-location queries on a specific arrangement instance. It is possible of course to define a point-location object and to issue separate queries on the arrangement. However, as explained in Section 31.3.1, choosing a simple point-location strategy (either the naive or the walk strategy) means inefficient queries, while the more sophisticated strategies need to construct auxiliary structures that incur considerable overhead in running time.
On the other hand, the arrangement package includes a free locate() function that accepts an arrangement a range of query points as its input and sweeps through the arrangement to locate all query points in one pass. The function outputs the query results as pairs, where each pair is comprised of a query point and a Cgal Object that represents the cell containing the point (see Section 31.3.1). The output pairs are sorted in increasing xy-lexicographical order of the query point.
The batched point-location operation can be performed in O((m+N)log (m+N)) time, where N is the number of edges in the arrangement. This means that when the number m of point-location queries is of the same order of magnitude as N, this operation is more efficient than issuing separate queries. This suggestion is also backed up by experimental results. Moreover, the batched point-location operation is also advantageous as it does not have to construct and maintain additional data structures.
The following program issues a batched point-location query, which is essentially equivalent to the six separate queries performed in point_location.cpp (see Section 31.3.1):
File: examples/Arrangement_on_surface_2/batched_point_location.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_batched_point_location.h>
#include <list>
#include "point_location_utils.h"
typedef CGAL::MP_Float Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef std::pair<Point_2, CGAL::Object> Query_result;
int main ()
{
// Construct the arrangement.
Arrangement_2 arr;
construct_segments_arr (arr);
// Perform a batched point-location query.
std::list<Point_2> query_points;
std::list<Query_result> results;
query_points.push_back (Point_2 (1, 4));
query_points.push_back (Point_2 (4, 3));
query_points.push_back (Point_2 (6, 3));
query_points.push_back (Point_2 (3, 2));
query_points.push_back (Point_2 (5, 2));
query_points.push_back (Point_2 (1, 0));
locate (arr, query_points.begin(), query_points.end(),
std::back_inserter (results));
// Print the results.
std::list<Query_result>::const_iterator res_iter;
Arrangement_2::Vertex_const_handle v;
Arrangement_2::Halfedge_const_handle e;
Arrangement_2::Face_const_handle f;
for (res_iter = results.begin(); res_iter != results.end(); ++res_iter) {
std::cout << "The point (" << res_iter->first << ") is located ";
if (CGAL::assign (f, res_iter->second)) {
// The current qeury point is located inside a face:
if (f->is_unbounded())
std::cout << "inside the unbounded face." << std::endl;
else
std::cout << "inside a bounded face." << std::endl;
}
else if (CGAL::assign (e, res_iter->second)) {
// The current qeury point is located on an edge:
std::cout << "on an edge: " << e->curve() << std::endl;
}
else if (CGAL::assign (v, res_iter->second)) {
// The current qeury point is located on a vertex:
if (v->is_isolated())
std::cout << "on an isolated vertex: " << v->point() << std::endl;
else
std::cout << "on a vertex: " << v->point() << std::endl;
}
}
return 0;
}
31.4 Free Functions in the Arrangement Package
In Section 31.2 we reviewed in details the Arrangement_2 class, which represents two-dimensional subdivisions induced by planar curves, and mentioned that its interface is minimal in the sense that the member functions hardly perform any geometric algorithms and are mainly used for maintaining the topological structure of the subdivision. In this section we explain how to utilize the free (global) functions that operate on arrangements. The implementation of these operations typically require non-trivial geometric algorithms or load some extra requirements on the traits class.
31.4.1 Incremental Insertion Functions
Inserting Non-Intersecting Curves
In Section 31.2 we explained how to construct arrangements of x-monotone curves that are pairwise disjoint in their interior, when the location of the segment endpoints in the arrangement is known. Here we relax this constraint, and allow the location of the inserted x-monotone curve endpoints to be arbitrary, as it may be unknown at the time of insertion. We retain, for the moment, the requirement that the interior of the inserted curve is disjoint from all existing arrangement edges and vertices.
The free function insert_non_intersecting_curve(arr, c, pl) inserts the x-monotone curve c into the arrangement arr, with the precondition that the interior of c is disjoint from all arr's existing edges and vertices. The third argument pl is a point-location object attached to the arrangement, which is used for performing the insertion. It locates both curve endpoints in the arrangement, where each endpoint is expected to either coincide with an existing vertex or lie inside a face. It is possible to invoke one of the specialized insertion functions (see Section 31.2), based on the query results, and insert c at its proper position.9 The insertion operation thus hardly requires any geometric operations on top on the ones needed to answer the point-location queries. Moreover, it is sufficient that the arrangement class is instantiated with a traits class that models the ArrangementBasicTraits_2 concept (or the ArrangementLandmarkTraits_2 concept, if the landmark point-location strategy is used), which does not have to support the computation of intersection points between curves.
The variant insert_non_intersecting_curve(arr, c) is also available. Instead of accepting a user-defined point-location object, it defines a local instance of the walk point-location class and uses it to insert the curve.
Inserting x-Monotone Curves
The insert_non_intersecting_curve() function is very efficient, but its preconditions on the input curves are still rather restricting. Let us assume that the arrangement is instantiated with a traits class that models the refined ArrangementXMonotoneTraits_2 concept and supports intersection computations (see Section 31.6 for the exact details). Given an x-monotone curve, it is sufficient to locate its left endpoint in the arrangement and to trace its zone, namely the set of arrangement features crossing the curve, until the right endpoint is reached. Each time the new curve c crosses an existing vertex or an edge, the curve is split into subcurves (in the latter case, we have to split the curve associated with the existing halfedge as well) and associate new edges with the resulting subcurves. Recall that an edge is represented by a pair of twin halfedges, so we split it into two halfedge pairs.
The free function insert(arr, c, pl) performs this insertion operation. It accepts an x-monotone curve c, which may intersect some of the curves already in the arrangement arr, and inserts it into the arrangement by computing its zone. Users may supply a point-location object pl, or use the default walk point-location strategy (namely, the variant insert(arr, c) is also available). The running-time of this insertion function is proportional to the complexity of the zone of the curve c.
Inserting General Curves
So far all our examples were of arrangements of line segments, where the Arrangement_2 template was instantiated with the Arr_segment_traits_2 class. In this case, the fact that insert() accepts an x-monotone curve does not seem to be a restriction, as all line segments are x-monotone (note that we consider vertical line segments to be weakly x-monotone).
Suppose that we construct an arrangement of circles. A circle is obviously not x-monotone, so we cannot insert it in the same way we inserted x-monotone curves. 10 However, it is possible to subdivide each circle into two x-monotone circular arcs (its upper half and its lower half) and to insert each x-monotone arc separately.
The free function insert() also supports general curve and not necessarily x-monotone curves. In this case it requires that the traits class used by the arrangement arr to be a model of the concept ArrangementTraits_2, which refines the ArrangementXMonotoneTraits_2 concept. It has to define an additional Curve_2 type (which may differ from the X_monotone_curve_2 type), and support the subdivision of curves of this new type into x-monotone curves (see the exact details in Section 31.6). The insert(arr, c, pl) function performs the insertion of the curve c, which does not need to be x-monotone, into the arrangement by subdividing it (if needed) into x-monotone subcurves and inserting each one separately. Users may supply a point-location object pl, or use the default walk point-location strategy by calling insert(arr, c).
Inserting Points
The arrangement class enables us to insert a point as an isolated vertex in a given face. The free function insert_point(arr, p, pl) inserts a vertex into arr that corresponds to the point p at an arbitrary location. It uses the point-location object pl to locate the point in the arrangement (by default, the walk point-location strategy is used), and acts according to the result as follows:
- If p is located inside a face, it is inserted as an isolated vertex inside this face.
- If p lies on an edge, the edge is split to create a vertex associated with p.
- Otherwise, p coincides with an existing vertex and we are done.
The arrangement arr should be instantiated with a traits class that models the ArrangementXMonotoneTraits_2 concept, as the insertion operation may involve splitting curves.
An Example
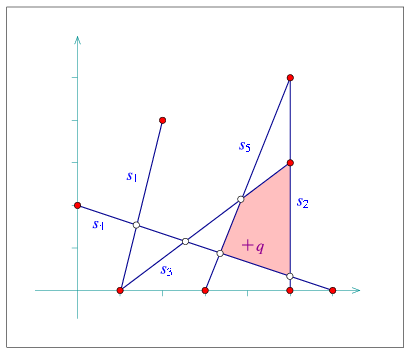
The program below constructs an arrangement of intersecting line-segments. We know that s1 and s2 do not intersect, so we use insert_non_intersecting_curve() to insert them into the empty arrangement. The rest of the segments are inserted using insert(). The resulting arrangement consists of 13 vertices, 16 edges, and 5 faces, as can be seen in Figure 31.8.
In the earlier examples, all arrangement vertices corresponded to segment endpoints. In this example we have additional vertices that correspond to intersection points between two segments. The coordinates of these intersection points are rational numbers, if the input coordinates are rational (or integer). Therefore, the Quotient<int> number type is used to represent the coordinates:
File: examples/Arrangement_on_surface_2/incremental_insertion.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_walk_along_line_point_location.h>
#include "arr_print.h"
typedef CGAL::Quotient<int> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_walk_along_line_point_location<Arrangement_2> Walk_pl;
int main ()
{
// Construct the arrangement of five intersecting segments.
Arrangement_2 arr;
Walk_pl pl(arr);
Segment_2 s1 (Point_2(1, 0), Point_2(2, 4));
Segment_2 s2 (Point_2(5, 0), Point_2(5, 5));
Segment_2 s3 (Point_2(1, 0), Point_2(5, 3));
Segment_2 s4 (Point_2(0, 2), Point_2(6, 0));
Segment_2 s5 (Point_2(3, 0), Point_2(5, 5));
insert_non_intersecting_curve (arr, s1, pl);
insert_non_intersecting_curve (arr, s2, pl);
insert (arr, s3, pl);
insert (arr, s4, pl);
insert (arr, s5, pl);
// Print the size of the arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Perform a point-location query on the resulting arrangement and print
// the boundary of the face that contains it.
Point_2 q (4, 1);
CGAL::Object obj = pl.locate (q);
Arrangement_2::Face_const_handle f;
CGAL_assertion_code (bool success =) CGAL::assign (f, obj);
CGAL_assertion (success);
std::cout << "The query point (" << q << ") is located in: ";
print_face<Arrangement_2> (f);
return 0;
}
Other Zone Related Functions
In this section we have described so far free functions that insert curves and points to a given arrangement. Now we will describe functions that don't insert curves or points to an arrangement nor do they change the arrangement, but they are closely related to the incremental insertion functions as they also use the zone algorithm.
The free function do_intersect() checks if a given curve or x-monotone curve intersects an existing arrangement's edges or vertices. If the give curve is not an x-monotone curve then the function subdivides the given curve into x-monotone subcurves and isolated vertices . Each subcurve is in turn checked for intersection. The function uses the zone algorithm to check if the curve intersects the arrangement. First, the curve's left endpoint is located. Then, its zone is computed starting from its left endpoint location. The zone computation terminates when an intersection with an arrangement's edge/vertex is found or when the right endpoint is reached. A given point-location object is used for locating the left endpoint of the given curve in the existing arrangement. By default, the function uses the ``walk along line'' point-location strategy - namely an instance of the class Arr_walk_along_line_point_location. If the given curve is x-monotone then the traits class must model the ArrangementXMonotoneTraits_2 concept. If the curve is not x-monotone curve then the traits class must model the ArrangementTraits_2 concept.
The zone() function computes the zone of a given x-monotone curve in a given arrangement. Meaning, it outputs all the arrangement's elements (vertices, edges and faces) that the x-monotone curve intersects in the order that they are discovered when traversing the x-monotone curve from left to right. The function uses a given point-location object to locate the left endpoint of the given x-monotone curve. By default, the function uses the ``walk along line'' point-location strategy. The function requires that the traits class will model the ArrangementXMonotoneTraits_2 concept.
31.4.2 Aggregated Insertion Functions
Let us assume that we have to insert a set of m input curves into an arrangement. It is possible to do this incrementally, inserting the curves one by one, as shown in the previous section. However, the arrangement package provides three free functions that aggregately insert a range of curves into an arrangement:
- insert_non_intersecting_curves(arr, begin, end) inserts a range of x-monotone curves given by the input iterators [begin, end) into an arrangement arr. The x-monotone curves should be pairwise disjoint in their interior and also interior-disjoint from all existing edges and vertices of arr.
- insert(arr, begin, end) inserts a range of general (not necessarily x-monotone) curves of type Curve_2 or X_monotone_curve_2 that may intersect one another, given by the input iterators [begin, end), into the arrangement arr.
We distinguish between two cases: (i) The given arrangement arr is empty (has only an unbounded face), so we have to construct it from scratch. (ii) We have to insert m input curves to a non-empty arrangement arr.
In the first case, we sweep over the input curves, compute their intersection points and construct the Dcel that represents their planar arrangement. This process is performed in O((m + k)log m) time, where k is the total number of intersection points. The running time is asymptotically better than the time needed for incremental insertion, if the arrangement is relatively sparse (when k is bounded by (m2)/(log m)), but in practice it is recommended to use this aggregated construction process even for dense arrangements, since the sweep-line algorithm needs less geometric operations compared to the incremental insertion algorithms and hence typically runs much faster in practice.
Another important advantage the aggregated insertion functions have is that they do not issue point-location queries. Thus, no point-location object needs to be attached to the arrangement. As explained in Section 31.3.1, there is a trade-off between construction time and query time in each of the point-location strategies, which affects the running times of the incremental insertion process. Naturally, this trade-off is irrelevant in case of aggregated insertion as above.
The example below shows how to construct the arrangement of line segments depicted in Figure 31.8 and built incrementally in incremental_insertion.cpp, as shown in the previous section. We use the aggregated insertion function insert() as we deal with line segments. Note that no point-location object needs to be defined and attached to the arrangement:
File: examples/Arrangement_on_surface_2/aggregated_insertion.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <list>
typedef CGAL::Quotient<int> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
// Construct the arrangement of five intersecting segments.
Arrangement_2 arr;
std::list<Segment_2> segments;
segments.push_back (Segment_2 (Point_2(1, 0), Point_2(2, 4)));
segments.push_back (Segment_2 (Point_2(5, 0), Point_2(5, 5)));
segments.push_back (Segment_2 (Point_2(1, 0), Point_2(5, 3)));
segments.push_back (Segment_2 (Point_2(0, 2), Point_2(6, 0)));
segments.push_back (Segment_2 (Point_2(3, 0), Point_2(5, 5)));
insert (arr, segments.begin(), segments.end());
// Print the size of the arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
In case we have to insert a set of m curves into an existing arrangement, where we denote the number of edges in the arrangement by N. As a rule of thumb, if m = o(√N), we insert the curves one by one. For larger input sets, we use the aggregated insertion procedures.
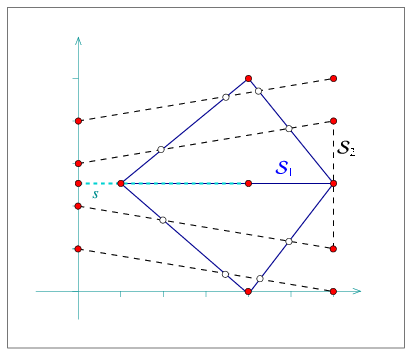
In the example below we aggregately construct an arrangement of a set S1 containing five line segments. Then we insert a single segment using the incremental insertion function. Finally, we add a set S2 with five more line segments in an aggregated fashion. Notice that the line segments of S1 are pairwise interior-disjoint, so we use insert_non_intersecting_curves(). S2 also contain pairwise interior-disjoint segments, but as they intersect the existing arrangement, we have to use insert() to insert them. Also note that the single segment s we insert incrementally overlaps an existing arrangement edge:
File: examples/Arrangement_on_surface_2/global_insertion.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_naive_point_location.h>
#include "arr_print.h"
typedef CGAL::Quotient<CGAL::MP_Float> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_naive_point_location<Arrangement_2> Naive_pl;
int main ()
{
// Construct the arrangement of five intersecting segments.
Arrangement_2 arr;
Segment_2 S1 [5];
S1[0] = Segment_2 (Point_2 (1, 2.5), Point_2 (4, 5));
S1[1] = Segment_2 (Point_2 (1, 2.5), Point_2 (6, 2.5));
S1[2] = Segment_2 (Point_2 (1, 2.5), Point_2 (4, 0));
S1[3] = Segment_2 (Point_2 (4, 5), Point_2 (6, 2.5));
S1[4] = Segment_2 (Point_2 (4, 0), Point_2 (6, 2.5));
insert_non_intersecting_curves (arr, S1, S1 + 5);
// Perform an incremental insertion of a single overlapping segment.
Naive_pl pl (arr);
insert (arr, Segment_2 (Point_2 (0, 2.5), Point_2 (4, 2.5)), pl);
// Aggregately insert an additional set of five segments.
Segment_2 S2 [5];
S2[0] = Segment_2 (Point_2 (0, 4), Point_2 (6, 5));
S2[1] = Segment_2 (Point_2 (0, 3), Point_2 (6, 4));
S2[2] = Segment_2 (Point_2 (0, 2), Point_2 (6, 1));
S2[3] = Segment_2 (Point_2 (0, 1), Point_2 (6, 0));
S2[4] = Segment_2 (Point_2 (6, 1), Point_2 (6, 4));
insert (arr, S2, S2 + 5);
// Print the size of the arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
The number type used in the example above, Quotient<MP_Float>, is comprised of a numerator and a denominator of type MP_Float, namely floating-point numbers with unbounded mantissa. This number type is therefore capable of exactly computing the intersection points as long as the segment endpoints are given as floating-point numbers.
31.4.3 Removing Vertices and Edges
The free functions remove_vertex() and remove_edge() handle the removal of vertices and edges from an arrangement. The difference between these functions and the member functions of the Arrangement_2 template having the same name is that they allow the merger of two curves associated with adjacent edges to form a single edge. Thus, they require that the traits class that instantiates the arrangement instance is a model of the refined ArrangementXMonotoneTraits_2 concept (see Section 31.6).
The function remove_vertex(arr, v) removes the vertex v from the given arrangement arr, where v is either an isolated vertex or is a redundant vertex - namely, it has exactly two incident edges that are associated with two curves that can be merged to form a single x-monotone curve. If neither of the two cases apply, the function returns an indication that it has failed to remove the vertex.
The function remove_edge(arr, e) removes the edge e from the arrangement by simply calling arr.remove_edge(e) (see Section 31.2.3). In addition, if either of the end vertices of e becomes isolated or redundant after the removal of the edge, it is removed as well.
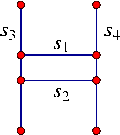
File: examples/Arrangement_on_surface_2/global_removal.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_naive_point_location.h>
#include "arr_print.h"
typedef int Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef Arrangement_2::Vertex_handle Vertex_handle;
typedef Arrangement_2::Halfedge_handle Halfedge_handle;
typedef CGAL::Arr_naive_point_location<Arrangement_2> Naive_pl;
int main ()
{
// Create an arrangement of four line segments forming an H-shape:
Arrangement_2 arr;
Naive_pl pl (arr);
Segment_2 s1 (Point_2 (1, 3), Point_2 (4, 3));
Halfedge_handle e1 = arr.insert_in_face_interior (s1, arr.unbounded_face());
Segment_2 s2 (Point_2 (1, 4), Point_2 (4, 4));
Halfedge_handle e2 = arr.insert_in_face_interior (s2, arr.unbounded_face());
Segment_2 s3 (Point_2 (1, 1), Point_2 (1, 6));
Segment_2 s4 (Point_2 (4, 1), Point_2 (4, 6));
insert (arr, s3, pl);
insert (arr, s4, pl);
std::cout << "The initial arrangement:" << std::endl;
print_arrangement (arr);
// Remove the horizontal edge from the arrangement, and its end vertices:
Vertex_handle v1 = e1->source(), v2 = e1->target();
arr.remove_edge (e1);
remove_vertex (arr, v1);
remove_vertex (arr, v2);
// Remove the second horizontal edge e2 from the arrangement:
remove_edge (arr, e2);
std::cout << "The final arrangement:" << std::endl;
print_arrangement (arr);
return 0;
}
31.5 Arrangements of Unbounded Curves
Previous sections dealt only with arrangements of line segments, namely of bounded curves. Such arrangements always have one unbounded face that contains all other arrangement features. This section explains how to construct arrangements of unbounded curves, such as lines and rays.
31.5.1 Basic Manipulation and Traversal Methods
Consider the arrangement induced by the two lines y = x and y = -x. These two lines intersect at the origin, such that the arrangement contains a single vertex v = (0,0), with four infinite rays emanating from it. Each ray corresponds to an arrangement edge, and these edges subdivide the plane into four unbounded faces. Consider a halfedge pair that represents one of the edges. The source vertex of one of these halfedges is v and its target is at infinity, while the other has its source at infinity and v is its target.
If e is an object of the nested type Arrangement_2::Halfedge, then the predicates e.source_at_infinity() and e.target_at_infinity() indicate whether the halfedge represents a curve with an infinite end. In general there is no need to access the source (or the target) of a halfedge if it lies at infinity, since this vertex is not associated with any valid point. Similarly, calling arr.number_of_vertices() for an arrangement object arr counts only the vertices associated with finite points, and ignores vertices at infinity (and the range [vertices_begin(), vertices_end()) contains only finite vertices). The method arr.number_of_vertices_at_infinity() counts the number of vertices at infinity.
As mentioned above, arrangements of unbounded curves usually have more than one unbounded face. The function arr.number_of_unbounded_faces() returns the number of unbounded arrangement faces (Thus, arr.number_of_faces() - arr.number_of_unbounded_faces() is the number of bounded faces). The functions arr.unbounded_faces_begin() and arr.unbounded_faces_end() return iterators of type Arrangement_2::Unbounded_face_iterator that specify the range of unbounded faces. Naturally, the value-type of this iterator is Arrangement_2::Face.
The specialized insertion functions listed in Section 31.2.3.1 can also be used for inserting x-monotone unbounded curves, provided that they are interior-disjoint from any subcurve that already exists in the arrangement. For example, if you wish to insert a ray r emanating from (0,0) in the direction of (1,0), to the arrangement of y = -x and y = x, you can use the function arr.insert_from_left_vertex(), as the left endpoint of r is already associated with an arrangement vertex. Other edge-manipulation functions can also be applied on edges associated with unbounded curves.
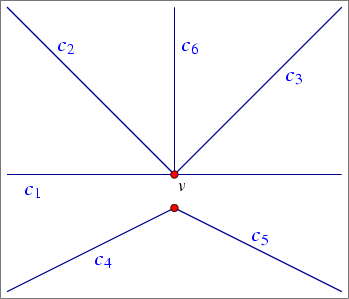
The following example demonstrates the use of the insertion function for pairwise interior-disjoint unbounded curves. In this example we use the traits class Arr_linear_traits_2<Kernel> to instantiate the Arrangement_2 template. This traits class is capable of representing line segments as well as unbounded linear curves (namely lines and rays). Observe that objects of the type X_monotone_curve_2 defined by this traits class are constructible from Line_2, Ray_2, and Segment_2 objects, as defined in the instantiated kernel.
The first three curves are inserted using the special insertion functions for x-monotone curves whose location in the arrangement is known. Notice that inserting an unbounded curve in the interior of an unbounded face, or from an existing vertex that represents the bounded end of the curve, may cause an unbounded face to split (this is never the case when inserting a bounded curve - compare with Section 31.2.3.1). Then, three additional rays are inserted incrementally, using the insertion function for x-monotone curves whose interior is disjoint from all arrangement features. Finally, the program prints the size of the arrangement (compare to the illustration in Figure 31.10) and the outer boundaries of its six unbounded faces:
File: examples/Arrangement_on_surface_2/unbounded_non_intersecting.cpp
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Arr_linear_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef int Number_type;
typedef CGAL::Simple_cartesian<Number_type> Kernel;
typedef CGAL::Arr_linear_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Segment_2 Segment_2;
typedef Traits_2::Ray_2 Ray_2;
typedef Traits_2::Line_2 Line_2;
typedef Traits_2::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef Arrangement_2::Vertex_handle Vertex_handle;
typedef Arrangement_2::Halfedge_handle Halfedge_handle;
int main ()
{
Arrangement_2 arr;
// Insert a line in the (currently single) unbounded face of the arrangement,
// then split it into two at (0,0). Assign v to be the split point.
X_monotone_curve_2 c1 = Line_2 (Point_2 (-1, 0), Point_2 (1, 0));
Halfedge_handle e1 = arr.insert_in_face_interior (c1,
arr.unbounded_face());
X_monotone_curve_2 c1_left = Ray_2 (Point_2 (0, 0), Point_2 (-1, 0));
X_monotone_curve_2 c1_right = Ray_2 (Point_2 (0, 0), Point_2 (1, 0));
e1 = arr.split_edge (e1, c1_left, c1_right);
Vertex_handle v = e1->target();
CGAL_assertion (! v->is_at_open_boundary());
// Add two more rays using the specialized insertion functions.
X_monotone_curve_2 c2 = Ray_2 (Point_2 (0, 0), Point_2 (-1, 1));
X_monotone_curve_2 c3 = Ray_2 (Point_2 (0, 0), Point_2 (1, 1));
arr.insert_from_right_vertex (c2, v);
arr.insert_from_left_vertex (c3, v);
// Insert three more interior-disjoint rays.
X_monotone_curve_2 c4 = Ray_2 (Point_2 (0, -1), Point_2 (-2, -2));
X_monotone_curve_2 c5 = Ray_2 (Point_2 (0, -1), Point_2 (2, -2));
X_monotone_curve_2 c6 = Ray_2 (Point_2 (0, 0), Point_2 (0, 1));
insert_non_intersecting_curve (arr, c4);
insert_non_intersecting_curve (arr, c5);
insert_non_intersecting_curve (arr, c6);
// Print out the size of the resulting arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< " (plus " << arr.number_of_vertices_at_infinity()
<< " at infinity)"
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces()
<< " (" << arr.number_of_unbounded_faces() << " unbounded)"
<< std::endl << std::endl;
// Print the outer CCBs of the unbounded faces.
Arrangement_2::Face_const_iterator fit;
Arrangement_2::Ccb_halfedge_const_circulator first, curr;
Arrangement_2::Halfedge_const_handle he;
int k = 1;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit, k++) {
if (! fit->is_unbounded())
continue;
std::cout << "Face no. " << k << ": ";
curr = first = fit->outer_ccb();
if (! curr->source()->is_at_open_boundary())
std::cout << "(" << curr->source()->point() << ")";
do {
he = curr;
if (! he->is_fictitious())
std::cout << " [" << he->curve() << "] ";
else
std::cout << " [ ... ] ";
if (! he->target()->is_at_open_boundary())
std::cout << "(" << he->target()->point() << ")";
++curr;
} while (curr != first);
std::cout << std::endl;
}
return 0;
}
31.5.2 Free Functions
In principle, all queries and operations that relate to arrangements of bounded curves can also be applied to arrangements of unbounded curves. For example, it is possible to issue point-location and vertical ray-shooting queries (see also Section 31.3) on arrangements of lines, where the only restriction is that the query point has finite coordinates.11
In the following example we show how an arrangement of unbounded lines is utilized to solve the following problem: Given a set of points, does the set contain at least three collinear points? In this example a set of input points is read from a file. The file points.dat is used by default. It contains definitions of 100 points randomly selected on the grid [-10000,10000] × [-10000,10000]. We construct an arrangement of the dual lines, where the line p* dual to the point p = (px, py) is given by the equation y = px*x - py, and check whether three (or more) of the dual lines intersect at a common point, by searching for a (dual) vertex, whose degree is greater than 4. If such a vertex exists, then there are at least three dual lines that intersect at a common point, which implies that there are at least three collinear points.
File: examples/Arrangement_on_surface_2/dual_lines.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_linear_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <cstdlib>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_linear_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Line_2 Line_2;
typedef Traits_2::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main (int argc, char *argv[])
{
// Get the name of the input file from the command line, or use the default
// points.dat file if no command-line parameters are given.
const char * filename = (argc > 1) ? argv[1] : "points.dat";
// Open the input file.
std::ifstream in_file (filename);
if (! in_file.is_open()) {
std::cerr << "Failed to open " << filename << "!" << std::endl;
return 1;
}
// Read the points from the file, and consturct their dual lines.
// The input file format should be (all coordinate values are integers):
// <n> // number of point.
// <x_1> <y_1> // point #1.
// <x_2> <y_2> // point #2.
// : : : :
// <x_n> <y_n> // point #n.
std::vector<Point_2> points;
std::list<X_monotone_curve_2> dual_lines;
unsigned int n;
in_file >> n;
points.resize(n);
unsigned int k;
for (k = 0; k < n; ++k) {
int px, py;
in_file >> px >> py;
points[k] = Point_2 (px, py);
// The line dual to the point (p_x, p_y) is y = p_x*x - p_y,
// or: p_x*x - y - p_y = 0:
dual_lines.push_back (Line_2 (Number_type(px),
Number_type(-1),
Number_type(-py)));
}
in_file.close();
// Construct the dual arrangement by aggragately inserting the lines.
Arrangement_2 arr;
insert (arr, dual_lines.begin(), dual_lines.end());
std::cout << "The dual arrangement size:" << std::endl
<< "V = " << arr.number_of_vertices()
<< " (+ " << arr.number_of_vertices_at_infinity()
<< " at infinity)"
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces()
<< " (" << arr.number_of_unbounded_faces()
<< " unbounded)" << std::endl;
// Look for a vertex whose degree is greater than 4.
Arrangement_2::Vertex_const_iterator vit;
bool found_collinear = false;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
if (vit->degree() > 4) {
found_collinear = true;
break;
}
}
if (found_collinear)
std::cout << "Found at least three collinear points in the input set."
<< std::endl;
else
std::cout << "No three collinear points are found in the input set."
<< std::endl;
// Pick two points from the input set, compute their midpoint and insert
// its dual line into the arrangement.
Kernel ker;
const int k1 = std::rand() % n, k2 = (k1 + 1) % n;
Point_2 p_mid = ker.construct_midpoint_2_object() (points[k1],
points[k2]);
X_monotone_curve_2 dual_p_mid = Line_2 (Number_type(p_mid.x()),
Number_type(-1),
Number_type(-p_mid.y()));
insert (arr, dual_p_mid);
// Make sure that we now have three collinear points.
found_collinear = false;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
if (vit->degree() > 4) {
found_collinear = true;
break;
}
}
CGAL_assertion (found_collinear);
return (0);
}
Note that there are no three collinear points among the points defined in the input file points.dat. In the second part of the example the existence of collinearity is forced and verified as follows. A line dual to the midpoint of two randomly selected points is introduced, and inserted into the arrangement. This operation is followed by a test that verifies that a vertex of degree greater than 4 exists. This implied that collinearity indeed exists as explained above.
31.5.3 Representation of Unbounded Arrangements
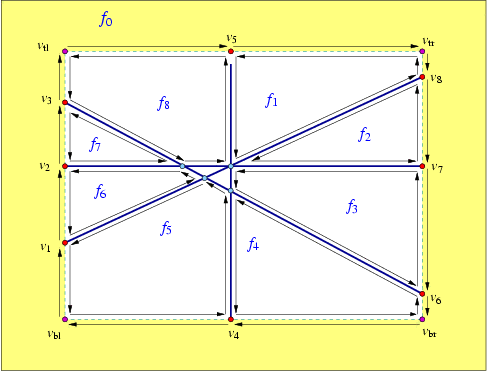
Given a set C of unbounded curves, a simple approach for representing the arrangement induced by C would be to clip the unbounded curves using an axis-parallel rectangle that contains all finite curve endpoints and intersection points between curves in C. This process would result in a set C of bounded curves (line segments if C contains lines and rays), and it would be straightforward to compute the arrangement induced by this set. However, we would like to operate directly on the unbounded curves without having to preprocess them. Therefore, we use an implicit bounding rectangle embedded in the Dcel structure. Figure 31.11 shows the arrangement of four lines that subdivide the plane into eight unbounded faces and two bounded ones. Notice that in this case the unbounded faces have outer boundaries, and the halfedges along these outer CCBs are drawn as arrows. The bounding rectangle is drawn with a dashed line. The vertices v1,v2, … ,v8, which represent the unbounded ends of the four lines, and lie on the bounding rectangle, actually exist at infinity, and the halfedges connecting them are fictitious, and represent portions of the bounding rectangle. Note that the outer CCBs of the unbounded faces contain fictitious halfedges. The twins of these halfedges form together one connected component that corresponds to the entire bounding rectangle, which forms a single hole in a face f0. We say that f0 is fictitious, as it does not correspond to a real two-dimensional cell of the arrangement.
Observe that there are four extra vertices at infinity that do not lie on any curve; they are denoted as vbl, vtl, vbr, and vtr, and represent the bottom-left, top-left, bottom-right, and top-right corners of the bounding rectangle, respectively. Similarly, there are fictitious halfedges that lie on the top, the bottom, the left, or the right edge of the bounding rectangle. When the arrangement is empty, there are exactly four pairs of fictitious halfedges, that divide the plane into two faces, namely a fictitious face lying outside of the bounding rectangle and a single unbounded face bounded by the bounding rectangle.
Summarizing the above, there are four types of arrangement vertices, which differ from one another by their location with respect to the bounding bounding rectangle:
- A vertex, associated with a point in ℝ2 whose coordinates are bounded. Such a vertex always lies inside the bounding rectangle.
- A vertex that represents an unbounded end of an x-monotone curve that is defined at x = -∞ or at x = ∞. In case of a horizontal line or a curve with a horizontal asymptote, the y-coordinate of the curve end may be finite (see for example the vertices v2 and v7 in Figure 31.11), but in general the curve end also goes to y = ± ∞ (see for instance the vertices v1, v3, v6 and v8 in Figure 31.11). For our convenience, we will always take a ``tall'' enough bounding rectangle and treat such vertices as lying on either the left or right rectangle edges (that is, if a curve is defined at x = -∞, its left end will be represented by a vertex on the left edge of the bounding rectangle, and if it is defined at x = ∞, its right end will be represented by a vertex of the right edge).
- A vertex that represent the unbounded end of a vertical line or of a curve with a vertical asymptote (finite x-coordinate and an unbounded y-coordinate). Such a vertex always lies on one of the horizontal edges of the bounding rectangle (either the bottom one if y = -∞, or the top one if y = ∞). The vertices v4 and v5 in Figure 31.11 are of this type.
- The fictitious vertices that represent the four corners of the bounding bounding rectangle.
The nested types defined in the Arrangement_2 class support the following methods, in addition to the ones listed in Section 31.2.2:
- The Vertex class provides three-valued predicates parameter_space_in_x() and parameter_space_in_y(), which return the location of the geometric embedding of the vertex in the parameter space. In particular, the former returns ARR_LEFT_BOUNDARY, ARR_INTERIOR, or ARR_RIGHT_BOUNDARY, and the latter returns ARR_BOTTOM_BOUNDARY, ARR_INTERIOR, or ARR_TOP_BOUNDARY. As the package currently supports only the case where the parameter space is the compactified plane, the former returns ARR_INTERIOR if the x-coordinate associated with the vertex is finite, ARR_LEFT_BOUNDARY if it is -∞, and ARR_RIGHT_BOUNDARY if it is ∞. The latter returns ARR_INTERIOR if the y-coordinate associated with the vertex is finite, ARR_BOTTOM_BOUNDARY if it is -∞, and ARR_TOP_BOUNDARY if it is ∞. The Boolean predicate is_at_open_boundary() is also provided. You can access the point associated with a vertex only if it is not a vertex at an open boundary (recall that a vertex at an open boundary is not associated with a Point_2 object).
- The nested Halfedge class provides the Boolean predicate is_fictitious(). The x-monotone curve associated with a halfedge can be accessed by the curve() method only if the halfedge is not fictitious.
- The nested Face class provides the Boolean predicate f.is_fictitious(). The method outer_ccb() has the precondition that the face is not fictitious. Note that non-fictitious unbounded faces always have valid CCBs (although this CCB may comprise only fictitious halfedge in case the arrangement contains only bounded curves).
The method arr.number_of_edges() does not count the number of fictitious edges, (which is always arr.number_of_vertices_at_infinity() + 4), and the iterators returned by arr.edges_begin() and arr.edges_end() specify a range of non-fictitious edges. Similarly, arr.number_of_faces() does not count the fictitious face. However, the Ccb_halfedge_circulator of the outer boundary of an unbounded face or the Halfegde_around_vertex_circulator of a vertex at infinity do traverse fictitious halfedges. For example, it is possible to traverse the outer boundaries of the unbounded arrangement edges using the following procedure:
Arrangement_2::Unbounded_face_const_iterator fit;
Arrangement_2::Ccb_halfedge_const_circulator first, curr;
Arrangement_2::Halfedge_const_handle he;
int k = 1;
for (fit = arr.unbounded_faces_begin();
fit != arr.unbounded_faces_end(); ++fit, k++)
{
std::cout << "Unbounded face no. " << k << ": ";
curr = first = fit->outer_ccb();
if (! curr->source()->is_at_infinity())
std::cout << "(" << curr->source()->point() << ")";
do
{
he = curr;
if (! he->is_fictitious())
std::cout << " [" << he->curve() << "] ";
else
std::cout << " [ ... ] ";
if (! he->target()->is_at_infinity())
std::cout << "(" << he->target()->point() << ")";
++curr;
} while (curr != first);
std::cout << std::endl;
}
31.6 Traits Classes
As mentioned in the introduction of this chapter, the traits class encapsulates the definitions of the geometric entities and implements the geometric predicates and constructions needed by the Arrangement_2 class and by its peripheral algorithms. We also mention throughout the chapter that there are different levels of requirements from the traits class, namely the traits class can model different concept refinement-levels.
31.6.1 The Hierarchy of Traits-Class Concepts
The Basic Concept
A model of the basic concept, ArrangementBasicTraits_2, needs to define the types Point_2 and X_monotone_curve_2, where objects of the first type are the geometric mapping of arrangement vertices, and objects of the latter type are the geometric mapping of edges. Such a model has to support in addition the following set of operations:
- Compare_x_2:
- Compares the x-coordinates of two points.
- Compare_xy_2:
- Compares two points lexicographically, by their x-coordinates and then (in case of equality) by their y-coordinates.
- Construct_min_vertex_2,Construct_max_vertex_2:
- Returns the left endpoint (similarly, the right endpoint) of an x-monotone curve.
- Compare_y_at_x_2:
- Given an x-monotone curve c and a point p that lies in its x-range, this predicate determines whether p lies below, above or on c.
- Compare_y_at_x_right_2:
- Given two x-monotone curves c1 and c2 that share a common left endpoint p, this predicate determines whether c1 lies above or under c2 immediately to the right of p, or whether the two curves coincide there.
- Equal_2:
- Checks two points and two curves for equality (two curves are equal if their graph is the same).
- Is_vertical_2:
- Determines whether an x-monotone curve is vertical.
Each model of the concept ArrangementBasicTraits_2 needs to define a tag named Has_left_category. It determines whether the traits class supports the following predicate:
- Compare_y_at_x_left_2:
- Given two x-monotone curves c1 and c2 that share a common right endpoint p, this predicate determines whether c1 lies above or under c2 immediately to the left of p, or whether the two curves coincide there.
The basic set of predicates is sufficient for constructing arrangements of x-monotone curves that do not reach or approach the boundary of the parameter space. The nature of the input curves, i.e., whether some of them are expected to reach or approach the left, right, bottom, or top side of the boundary of the parameter space, must be conveyed by the traits class. This is done through the definition of four additional nested types, namely Left_side_category, Right_side_category, Bottom_side_category, and Top_side_category. Each of those types must be convertible to the type Arr_oblivious_side_tag for the class to be a model of the concept ArrangementBasicTraits_2.
The Landmarks Concept
The landmark point-location strategy (see Section 31.3.1) needs its associated arrangement to be instantiated with a model of the refined ArrangementLandmarkTraits_2 traits concept. A model of this concept must define a fixed precision number type (typically double) and support the additional operations:
- Approximate_2:
- Given a point p, approximate the x and y-coordinates of p using the fixed precision number type. We use this operation for approximate computations - there are certain operations in the search for the location of the point that need not be exact and we can perform them faster than other operations.
- Construct_x_monotone_curve_2:
- Given two points p1 and p2, this predicate constructs an x-monotone curve connecting p1 and p2.
Supporting Intersecting x-Monotone Curves
A traits class that models the ArrangementXMonotoneTraits_2 concept, which refines the ArrangementBasicTraits_2 concept, has to support the following functions:
- Intersection_2:
- Computes all intersection points and overlapping sections of two given x-monotone curves. If possible, computes also the multiplicity of each intersection point.12 Knowing the multiplicity of an intersection point is not required, but it can speed up the arrangement construction.
- Split_2:
- Splits an x-monotone curve c into two subcurves at a point p lying in the interior of c.
- Are_mergeable_2:
- Given two x-monotone curve c1 and c2 that share a common endpoint, this predicate determines whether c1 and c2 are mergeable, that is, whether they can be merged to form a single continuous x-monotone curve of the type supported by the traits class.
- Merge_2:
- Merges two mergeable x-monotone curves.
Supporting Arbitrary Curves
The concept ArrangementTraits_2 refines the ArrangementXMonotoneTraits_2 concept by adding the notion of a general, not necessarily x-monotone (and not necessarily continuous) curve. A model of this concept must define the Curve_2 type and support the subdivision of a curve into a set of continuous x-monotone curves and isolated points using the predicate Make_x_monotone_2. For example, the curve C: (x2 + y2)(x2 + y2 - 1) = 0 is the unit circle (the loci of all points for which x2 + y2 = 1) with the origin (0,0) as a singular point in its interior. C should therefore be divided into two circular arcs (the upper part and the lower part of the unit circle) and a single isolated point.
Note that the refined model ArrangementTraits_2 is required only when using the free insert() functions (see Section 31.4), which accept a Curve_2 object in the incremental version, or a range of Curve_2 objects in the aggregated version. In all other cases it is sufficient to use a model of the ArrangementXMonotoneTraits_2 concept.
Supporting Unbounded Curves
An arrangement that supports unbounded x-monotone curves maintains an implicit bounding rectangle in the Dcel structure; see Section 31.5.3. The unbounded ends of vertical rays, vertical lines, and curves with vertical asymptotes are represented by vertices that lie on the bottom or top sides of this bounding rectangle. These vertices are not associated with points, but are associated with (finite) x-coordinates. The unbounded ends of all other curves are represented by vertices that lie on the left or right sides of this bounding rectangle. These vertices are not associated with points either. Edges connect these vertices and the four vertices that represents the corners of this bounding rectangle to form the rectangle.Several predicates are required to handle x-monotone curves that approach infinity and thus approach the boundary of the parameter space. These predicates are sufficient to handle not only curves embedded in an unbounded parameter space, but also curves embedded in a bounded parameter space with open boundaries. Let bl and br denote the x-coordinates of the left and right boundaries of the parameter space, respectively. Let bb and bt denote the y-coordinates of the bottom and top boundaries of the parameter space, respectively. Recall that currently the general code of the arrangement only supports the case where the parameter space is the entire compactified plane, thus bl = bb = -∞ and br = bt = +∞. Nonetheless, when the parameter space is bounded, it is the exact geometric embedding of the implicit bounding rectangle. In the following we assume that an x monotone curve C can be considered as a parametric curve C(t) = (X(t),Y(t)) defined over a closed, open, or half open interval with endpoints 0 and 1.
Models of the concept ArrangementOpenBoundaryTraits_2 handle curves that approach the boundary of the parameter space. This concept refines the concept ArrangementBasicTraits_2. The arrangement template instantiated with a traits class that models this concept can handle curves that are unbounded in any direction. If some curves inserted into an arrangement object are expected to be unbounded, namely, there exists d ∈ {0,1} such that lim t → dX(t) = ± ∞ or lim t → dy(t) = ± ∞ holds for at least one input curve C(t) = (X(t),Y(t)), the arrangement template must be instantiated with a model of the ArrangementOpenBoundaryTraits concept.13
All the four types Left_side_category, Right_side_category, Bottom_side_category, and Top_side_category nested in a model of the concept ArrangementOpenBoundaryTraits must be convertible to Arr_open_side_tag.14 For example, the Arr_rational_function_traits_2 traits-model supports unbounded curves; see Section 31.6.6. Thus, all four nested types are defined as Arr_open_side_tag. Adversely, all four types nested in the Arr_segment_traits_2 traits-model (see Section 31.6.2) are defined as Arr_oblivious_side_tag, as segments are always bounded.15
A model of the concept ArrangementOpenBoundaryTraits_2 must provide the additional predicates listed below. x-coordinates and y-coordinates are differently handled. This asymmetry is brought on by the various algorithms applied to arrangements, the input and output arguments of which are x-monotone curves. Indeed, all curves maintained by any arrangement are continuous weakly x-monotone curves. A non x-monotone curve is divided into x-monotone sub curves (and perhaps points) before it is inserted into an arrangement. This asymmetry is also reflected in the additional predicates listed below.
- Parameter_space_in_x_2:
- Given a parametric x-monotone curve C(t) = (X(t),Y(t)) and an enumerator that specifies either the minimum end or the maximum end of the curve, and thus maps to a parameter value d ∈ {0,1}, this predicate determines the location of the curve end along the x-dimension. Formally, the predicate determines whether lim t → d X(t) evaluates to bl, br, or a value in between.
- Compare_y_near_boundary_2:
- Given two x-monotone curves C1 and C2 and an enumerator i that specifies either the minimum ends or the maximum ends of the two curves, this predicate compares the y-coordinates of the curves near their respective ends. That is, the predicate compares the y-coordinates of the vertical projection of a point p onto C1 and onto C2. If the enumerator i specifies the minimum ends, the curves must approach the left boundary-side. In this case p is located far to the left, such that the result is invariant under a translation of p farther to the left. If i specifies the maximum ends, the curves must approach the right boundary-side. In that case p is located far to the right in a similar manner.
- Parameter_space_in_y_2:
- Given a parametric x-monotone curve C(t) = (X(t),Y(t)) and an enumerator that specifies either the minimum end or the maximum end of the curve, and thus maps to a parameter value d ∈ {0,1}, this predicate determines the location of the curve end along the y-dimension. Formally, the predicate determines whether lim t → d Y(t) evaluates to bb, bt, or a value in between.
- Compare_x_at_limit_2:
- Two versions of this predicate are provided: (i) Given a point p, a parametric x-monotone curve C(t) = (X(t),Y(t)), and an enumerator that specifies either the minimum end or the maximum end of the curve, and thus maps to a parameter value d ∈ {0,1}, this predicate compares the x-coordinate of p and lim t → d X(t). If the parameter space is unbounded, a precondition assures that C has a vertical asymptote at its d-end; that is lim t → d X(t) is finite. (ii) Given two parametric x-monotone curves C1(t) = (X1(t),Y1(t)) and C2(t) = (X2(t),Y2(t)) and two enumerators that specify either the minimum end or the maximum end of each curve, and thus map to parameter values d1 ∈ {0,1} and d2 ∈ {0,1} for C1 and for C2, respectively, this predicate compares lim t → d1 X1(t) and lim t → d2 X2(t). If the parameter space is unbounded, a precondition assures that C1 and C2 have vertical asymptote at their respective ends; that is lim t → d1 X1(t) and lim t → d2 X2(t) are finite.
- Compare_x_near_limit_2:
- Given two x-monotone curves C1 and C2 and an enumerator i that specifies either the minimum ends or the maximum ends of the two curves, this predicate compares the x-coordinates of the curves near their respective ends. That is, the predicate compares the x-coordinates of the horizontal projection of a point p onto C1 and onto C2. If the parameter space is unbounded, a precondition assures that C1 and C2 have vertical asymptote at their respective ends. Furthermore, both curves approach the same boundary-side, either the bottom or the top, at their respective ends. If both curves approach the bottom boundary-side, p is located far to the bottom, such that the result is invariant under a translation of p farther to the bottom. If both curves approach the top boundary-side, p is located far to the top in a similar manner. Another precondition assures that the x-coordinates of the limits of the curves at their respective ends are equal. That is, the predicate Compare_x_at_limit_2 applied to C1, C2, and i evaluates to EQUAL.
In the rest of this section we review the traits classes included in the public distribution of Cgal, that handle line segments, polylines, conic arcs, rational functions, and arcs of Bézier and algebraic curves. The last subsection overviews decorators for geometric traits classes distributed with Cgal, which extend other geometric traits-class by attaching auxiliary data with the geometric objects.
31.6.2 Traits Classes for Line Segments and Linear Objects
The Arr_segment_traits_2<Kernel> class used so far in most example programs in this chapter is a model of the concepts ArrangementTraits_2, ArrangementLandmarkTraits_2, and ArrangementDirectionalXMonotoneTraits_2; the later enables Boolean set operations. It is parameterized by a geometric kernel and uses the Kernel::Point_2 type as it point type. However, neither the Curve_2 nor the X_monotone_curve_2 types are identical to the Kernel::Segment_2 type. A kernel segment is typically represented by its two endpoints, and these may have a large bit-size representation, if the segment is intersected and split several times (in comparison with the representation of its original endpoints). The large representation may significantly slow down the various traits-class operations involving such a segment. In contrast, the Arr_segment_traits_2 represents a segment using its supporting line and the two endpoints, such that most computations are performed on the supporting line, which never changes as the segment is split. It also caches some additional information with the segment to speed up various predicates. An X_monotone_curve_2 object can still be constructed from two endpoints or from a kernel segment. Moreover, an X_monotone_curve_2 instance can also be casted or assigned to a Kernel::Segment_2 object. The two types are thus fully convertible to one another.
The Arr_segment_traits_2<Kernel> class is very efficient for maintaining arrangements of a large number of intersecting line segments, especially if it is instantiated with the appropriate geometric kernel. Using Cartesian<Gmpq> as the kernel type is generally a good choice; the coordinates of the segment endpoints are represented as exact rational numbers, and this ensures the robustness and correctness of any computation. However, if the Gmp library is not installed, it is possible to use the Quotient<MP_Float> number-type, provided by the support library of Cgal, which is somewhat less efficient.16
Exact computations are of course less efficient, compared to machine-precision floating-point arithmetic, so constructing an arrangement using the Cartesian<Gmpq> kernel (or, similarly, Cartesian<Quotient<MP_Float> >) is several times slower in comparison to a Simple_cartesian<double> kernel. However, in the latter case the correctness of the computation results is not guaranteed. In many cases it is possible to use filtered computations and benefit from both approaches, namely achieve fast running times with guaranteed results. In case we handle a set of line segments that have no degeneracies, namely no two segments share a common endpoint, and no three segments intersect at a common point - or alternatively, degeneracies exist but their number is relatively small - then filtered computation incur only a minor overhead compared to the floating-point arithmetic, while ensuring the correctness of the computation results.
 |
 |
| (a) | (b) |
In the following example we use the predefined Exact_predicates_exact_constructions_kernel for instantiating our segment-traits class. This kernel use interval arithmetic to filter the exact computations. The program reads a set of line segments with integer coordinates from a file and computes their arrangement. By default it opens the fan_grids.dat input-file, located in the examples folder, which contains 104 line segments that form four ``fan-like'' grids and induce a dense arrangement, as illustrated in Figure 31.12(a):
File: examples/Arrangement_on_surface_2/predefined_kernel.cpp
#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Timer.h>
#include <list>
#include <fstream>
typedef CGAL::Exact_predicates_exact_constructions_kernel Kernel;
typedef Kernel::FT Number_type;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main (int argc, char *argv[])
{
// Get the name of the input file from the command line, or use the default
// fan_grids.dat file if no command-line parameters are given.
const char * filename = (argc > 1) ? argv[1] : "fan_grids.dat";
// Open the input file.
std::ifstream in_file (filename);
if (! in_file.is_open()) {
std::cerr << "Failed to open " << filename << " ..." << std::endl;
return (1);
}
// Read the segments from the file.
// The input file format should be (all coordinate values are integers):
// <n> // number of segments.
// <sx_1> <sy_1> <tx_1> <ty_1> // source and target of segment #1.
// <sx_2> <sy_2> <tx_2> <ty_2> // source and target of segment #2.
// : : : :
// <sx_n> <sy_n> <tx_n> <ty_n> // source and target of segment #n.
std::list<Segment_2> segments;
unsigned int n;
in_file >> n;
unsigned int i;
for (i = 0; i < n; ++i) {
int sx, sy, tx, ty;
in_file >> sx >> sy >> tx >> ty;
segments.push_back (Segment_2 (Point_2 (Number_type(sx), Number_type(sy)),
Point_2 (Number_type(tx), Number_type(ty))));
}
in_file.close();
// Construct the arrangement by aggregately inserting all segments.
Arrangement_2 arr;
CGAL::Timer timer;
std::cout << "Performing aggregated insertion of "
<< n << " segments." << std::endl;
timer.start();
insert (arr, segments.begin(), segments.end());
timer.stop();
// Print the arrangement dimensions.
std::cout << "V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
std::cout << "Construction took " << timer.time()
<< " seconds." << std::endl;
return 0;
}
The arrangement package also offers a simpler alternative segment-traits class. The traits class Arr_non_caching_segment_basic_traits_2<Kernel> models the ArrangementBasicTraits_2 concept. It uses Kernel::Point_2 as its point type and Kernel::Segment_2 as its x-monotone curve type. As this traits class does not support intersecting and splitting segments, the kernel representation is sufficient. It is still less efficient than Arr_segment_traits_2 for constructing arrangements of pairwise disjoint line segments in many cases, as it performs no caching at all, but using this traits class may be preferable as it reduces the memory consumption a bit, since no extra data is stored with the line segments.
The class Arr_non_caching_segment_traits_2<Kernel> inherits from Arr_non_caching_segment_basic_traits_2<Kernel> and extends it to be a model of the concepts ArrangementTraits_2, ArrangementLandmarkTraits_2,and ArrangementDirectionalXMonotoneTraits_2. It may thus be used to construct arrangement of intersecting line segments, but as explained above, for efficiency reasons it is recommended to use it only when the arrangement is very sparse and contains hardly any intersection points.
In the following example we read an input file containing a set of line segments that are pairwise disjoint in their interior. As the segments do not intersect, no new points are constructed and we can instantiate the Arr_non_caching_segment_traits_basic_2<Kernel> class-template with the predefined Exact_predicates_inexact_constructions_kernel. Note that we use the insert_non_intersecting_curves() function to construct the arrangement. By default, the example opens the Europe.dat input-file, located in the examples folder, which contains more than 3000 line segments with floating-point coordinates that form the map of Europe, as depicted in Figure 31.12(b):
File: examples/Arrangement_on_surface_2/predefined_kernel_non_intersecting.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Arr_non_caching_segment_basic_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Timer.h>
#include <list>
#include <fstream>
typedef CGAL::Exact_predicates_inexact_constructions_kernel Kernel;
typedef Kernel::FT Number_type;
typedef CGAL::Arr_non_caching_segment_basic_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main (int argc, char *argv[])
{
// Get the name of the input file from the command line, or use the default
// Europe.dat file if no command-line parameters are given.
const char * filename = (argc > 1) ? argv[1] : "Europe.dat";
// Open the input file.
std::ifstream in_file (filename);
if (! in_file.is_open()) {
std::cerr << "Failed to open " << filename << " ..." << std::endl;
return (1);
}
// Read the segments from the file.
// The input file format should be (all coordinate values are double
// precision floating-point numbers):
// <n> // number of segments.
// <sx_1> <sy_1> <tx_1> <ty_1> // source and target of segment #1.
// <sx_2> <sy_2> <tx_2> <ty_2> // source and target of segment #2.
// : : : :
// <sx_n> <sy_n> <tx_n> <ty_n> // source and target of segment #n.
std::list<Segment_2> segments;
unsigned int n;
in_file >> n;
unsigned int i;
for (i = 0; i < n; ++i) {
double sx, sy, tx, ty;
in_file >> sx >> sy >> tx >> ty;
segments.push_back (Segment_2 (Point_2 (Number_type(sx), Number_type(sy)),
Point_2 (Number_type(tx), Number_type(ty))));
}
in_file.close();
// Construct the arrangement by aggregately inserting all segments.
Arrangement_2 arr;
CGAL::Timer timer;
std::cout << "Performing aggregated insertion of "
<< n << " segments." << std::endl;
timer.start();
insert_non_intersecting_curves (arr, segments.begin(), segments.end());
timer.stop();
// Print the arrangement dimensions.
std::cout << "V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
std::cout << "Construction took " << timer.time()
<< " seconds." << std::endl;
return 0;
}
The Arr_linear_traits_2<Kernel> class used for demonstrating the construction of arrangements of unbounded curves is capable of handling bounded and unbounded linear objects, namely lines, rays and line segments. It is parameterized by a geometric kernel and such that its nested Point_2 type is the same as the kernel point. The Curve_2 (and X_monotone_curve_2) type it defines is constructible from a Kernel::Line_2, a Kernel::Ray_2 or from a Kernel::Segment_2 object. Just like the default segment-traits class, the linear-traits class also use caching techniques to speed up its predicates and constructions.
31.6.3 The Polyline-Traits Class
The Arr_polyline_traits_2<SegmentTraits> class can be used to maintain arrangements of polylines (a.k.a. poly-segments), which are continuous piecewise linear curves. A polyline can be created from a range of points, where the i-th and (i+1)-st points in the range represent the endpoints of the i-th segment of the polyline. The polyline traits class is parameterized with a segment-traits class that supports the basic operations on segments.
Polylines are the simplest form of a curves that are not necessarily x-monotone. They can be used to approximate more complicated curves in a convenient manner, as the algebra needed to handle them is elementary - rational arithmetic is sufficient to construct an arrangement of polylines is an exact and robust manner. Note, however, that a single polyline can be split into many x-monotone polylines, and that the number of intersection points (or overlapping sections) between two polylines can also be large.
The polyline-traits class is a model of the ArrangementTraits_2 concept and of the ArrangementLandmarkTraits_2 concept. It inherits its point type from the segment-traits class, and defines the polyline type, which serves as its Curve_2. Polyline curve objects can be constructed from a range of points. They also enable the traversal over the range of defining points, whose first and past-the-end iterators can be obtained through the methods begin() and end(). The nested X_monotone_curve_2 type inherits from Curve_2. The points in an x-monotone curve are always stored in lexicographically increasing order of their coordinates.
The following example program constructs an arrangement of three polylines, as depicted in Figure 31.13. Note that most points defining the polylines are not associated with arrangement vertices. The arrangement vertices are either the extreme points of each x-monotone polyline or the intersection points between two polylines:
File: examples/Arrangement_on_surface_2/polylines.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_polyline_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <vector>
#include <list>
#include "arr_print.h"
typedef CGAL::Quotient<CGAL::MP_Float> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Segment_traits_2;
typedef CGAL::Arr_polyline_traits_2<Segment_traits_2> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Polyline_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
Arrangement_2 arr;
Point_2 points1[5];
points1[0] = Point_2 (0, 0);
points1[1] = Point_2 (2, 4);
points1[2] = Point_2 (3, 0);
points1[3] = Point_2 (4, 4);
points1[4] = Point_2 (6, 0);
Polyline_2 pi1 (&points1[0], &points1[5]);
std::list<Point_2> points2;
points2.push_back (Point_2 (1, 3));
points2.push_back (Point_2 (0, 2));
points2.push_back (Point_2 (1, 0));
points2.push_back (Point_2 (2, 1));
points2.push_back (Point_2 (3, 0));
points2.push_back (Point_2 (4, 1));
points2.push_back (Point_2 (5, 0));
points2.push_back (Point_2 (6, 2));
points2.push_back (Point_2 (5, 3));
points2.push_back (Point_2 (4, 2));
Polyline_2 pi2 (points2.begin(), points2.end());
std::vector<Point_2> points3 (4);
points3[0] = Point_2 (0, 2);
points3[1] = Point_2 (1, 2);
points3[2] = Point_2 (3, 6);
points3[3] = Point_2 (5, 2);
Polyline_2 pi3 (points3.begin(), points3.end());
insert (arr, pi1);
insert (arr, pi2);
insert (arr, pi3);
print_arrangement (arr);
return 0;
}
31.6.4 A Traits Class for Circular Arcs and Line Segments
Circles and circular arcs are the simplest form of non-linear curves. We handle circles whose centers have rational coordinates and whose squared radii is also rational. If we denote the circle center by (x0,y0) and its radius by r, then the equation of the circle - that is, (x - x0)2 + (y - y0)2 = r2 - has rational coefficients. The intersection points of two such circles are therefore solutions of a quadratic equation with rational coefficients, or algebraic numbers of degree 2. The same applies for intersection points between such a rational circle and a line, or a line segment, with rational coefficients (a line whose equation is ax + by + c = 0, where a, b and c are rational). Such numbers can be expressed as α+ β√γ, where α, β and γ are all rational numbers.
Arrangement of circular arcs and of line segment are very useful, as they occur in many applications. For example, when dilating a polygon by some radius we obtain a shape whose boundary is comprised of line segments, which correspond to dilated polygon edges, and circular arcs, which result from dilated polygon vertices. Using the arrangement of the boundary curves it is possible, for example, to compute the union of a set of dilated polygons.
The Arr_circle_segment_traits_2<Kernel> class-template is designed for efficient handling of arrangements of circular arcs and line segments. It is a model of the concepts ArrangementTraits_2 and ArrangementDirectionalXMonotoneTraits_2; the later enables Boolean set operations. Note that it is not a model of ArrangementLandmarkTraits_2 concept, so it is impossible to use the landmark point-location strategy. The traits class template is parameterized by a geometric kernel, and can handle arrangements of segments of Kernel::Circle_2 objects (full circles are also supported) or of Kernel::Line_2 objects - namely circular arcs and line segments. It is important to observe that the nested Point_2 type defined by the traits class, whose coordinates are typically algebraic numbers of degree 2, is not the same as the Kernel::Point_2 type, which is capable of representing a point with rational coordinates. The coordinates of a point are represented using the nested CoordNT number-type.
In the following example an arrangement of three full circles is constructed, as shown in Figure 31.14. Then, the vertex of maximal degree is searched for. The geometric mapping of this vertex is the point (4,3), as all three circles intersect at this point and the associated vertex has six incident edges:
File: examples/Arrangement_on_surface_2/circles.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_circle_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef Kernel::Circle_2 Circle_2;
typedef CGAL::Arr_circle_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::CoordNT CoordNT;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
// Create a circle centered at the origin with radius 5.
Kernel::Point_2 c1 = Kernel::Point_2 (0, 0);
Number_type sqr_r1 = Number_type (25); // = 5^2
Circle_2 circ1 = Circle_2 (c1, sqr_r1, CGAL::CLOCKWISE);
Curve_2 cv1 = Curve_2 (circ1);
// Create a circle centered at (7,7) with radius 5.
Kernel::Point_2 c2 = Kernel::Point_2 (7, 7);
Number_type sqr_r2 = Number_type (25); // = 5^2
Circle_2 circ2 = Circle_2 (c2, sqr_r2, CGAL::CLOCKWISE);
Curve_2 cv2 = Curve_2 (circ2);
// Create a circle centered at (4,-0.5) with radius 3.5 (= 7/2).
Kernel::Point_2 c3 = Kernel::Point_2 (4, Number_type (-1,2));
Number_type sqr_r3 = Number_type (49, 4); // = 3.5^2
Circle_2 circ3 = Circle_2 (c3, sqr_r3, CGAL::CLOCKWISE);
Curve_2 cv3 = Curve_2 (circ3);
// Construct the arrangement of the three circles.
Arrangement_2 arr;
insert (arr, cv1);
insert (arr, cv2);
insert (arr, cv3);
// Locate the vertex with maximal degree.
Arrangement_2::Vertex_const_iterator vit;
Arrangement_2::Vertex_const_handle v_max;
unsigned int max_degree = 0;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
if (vit->degree() > max_degree) {
v_max = vit;
max_degree = vit->degree();
}
}
std::cout << "The vertex with maximal degree in the arrangement is: "
<< "v_max = (" << v_max->point() << ") "
<< "with degree " << max_degree << "." << std::endl;
return 0;
}
The Curve_2 type nested in Arr_circle_segment_traits_2 can be used to represent circles, circular arcs, or line segments. Curve objects can therefore be constructed from a Kernel::Circle_2 object or from a Kernel::Segment_2 object. A circular arc is typically defined by a supporting circle and two endpoints, where the endpoints are instances of the Point_2 type, with rational or irrational coordinates. The orientation of the arc is determined by the orientation of the supporting circle. Similarly, we also support the construction of lines segments given their supporting line (of type Kernel::Line_2) and two endpoints, which may have irrational coordinates (unlike the Kernel::Segment_2 type).
Note that the Kernel::Circle_2 type represents a circle whose squared radius is rational, where the radius itself may be irrational. However, if the radius is known to be rational, it is advisable to use it, for efficiency reasons. It is therefore also possible to construct a circle, or a circular arc specifying the circle center (a Kernel::Point_2), its rational radius, and its orientation. Finally, we also support the construction of a circular arcs that is defined by two endpoints and an arbitrary midpoint that lies on the arc in between its endpoint. In this case, all three points are required to have rational coordinates (to be kernel points).
The following example demonstrates the usage of the various construction methods for circular arcs and line segments. Note the usage of the constructor of CoordNT (alpha, beta, gamma), which creates a degree-2 algebraic number whose value is α+ β√γ.
File: examples/Arrangement_on_surface_2/circular_arcs.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_circle_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef Kernel::Circle_2 Circle_2;
typedef Kernel::Segment_2 Segment_2;
typedef CGAL::Arr_circle_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::CoordNT CoordNT;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
std::list<Curve_2> curves;
// Create a circle centered at the origin with squared radius 2.
Kernel::Point_2 c1 = Kernel::Point_2 (0, 0);
Circle_2 circ1 = Circle_2 (c1, Number_type (2));
curves.push_back (Curve_2 (circ1));
// Create a circle centered at (2,3) with radius 3/2 - note that
// as the radius is rational we use a different curve constructor.
Kernel::Point_2 c2 = Kernel::Point_2 (2, 3);
curves.push_back (Curve_2 (c2, Number_type(3, 2)));
// Create a segment of the line (y = x) with rational endpoints.
Kernel::Point_2 s3 = Kernel::Point_2 (-2, -2);
Kernel::Point_2 t3 = Kernel::Point_2 (2, 2);
Segment_2 seg3 = Segment_2 (s3, t3);
curves.push_back (Curve_2 (seg3));
// Create a line segment with the same supporting line (y = x), but
// having one endpoint with irrational coefficients.
CoordNT sqrt_15 = CoordNT (0, 1, 15); // = sqrt(15)
Point_2 s4 = Point_2 (3, 3);
Point_2 t4 = Point_2 (sqrt_15, sqrt_15);
curves.push_back (Curve_2 (seg3.supporting_line(), s4, t4));
// Create a circular arc that correspond to the upper half of the
// circle centered at (1,1) with squared radius 3. We create the
// circle with clockwise orientation, so the arc is directed from
// (1 - sqrt(3), 1) to (1 + sqrt(3), 1).
Kernel::Point_2 c5 = Kernel::Point_2 (1, 1);
Circle_2 circ5 = Circle_2 (c5, 3, CGAL::CLOCKWISE);
CoordNT one_minus_sqrt_3 = CoordNT (1, -1, 3);
CoordNT one_plus_sqrt_3 = CoordNT (1, 1, 3);
Point_2 s5 = Point_2 (one_minus_sqrt_3, CoordNT (1));
Point_2 t5 = Point_2 (one_plus_sqrt_3, CoordNT (1));
curves.push_back (Curve_2 (circ5, s5, t5));
// Create a circular arc of the unit circle, directed clockwise from
// (-1/2, sqrt(3)/2) to (1/2, sqrt(3)/2). Note that we orient the
// supporting circle accordingly.
Kernel::Point_2 c6 = Kernel::Point_2 (0, 0);
CoordNT sqrt_3_div_2 = CoordNT (Number_type(0), Number_type(1,2), Number_type(3));
Point_2 s6 = Point_2 (Number_type (-1, 2), sqrt_3_div_2);
Point_2 t6 = Point_2 (Number_type (1, 2), sqrt_3_div_2);
curves.push_back (Curve_2 (c6, 1, CGAL::CLOCKWISE, s6, t6));
// Create a circular arc defined by two endpoints and a midpoint,
// all having rational coordinates. This arc is the upper-right
// quarter of a circle centered at the origin with radius 5.
Kernel::Point_2 s7 = Kernel::Point_2 (0, 5);
Kernel::Point_2 mid7 = Kernel::Point_2 (3, 4);
Kernel::Point_2 t7 = Kernel::Point_2 (5, 0);
curves.push_back (Curve_2 (s7, mid7, t7));
// Construct the arrangement of the curves.
Arrangement_2 arr;
insert (arr, curves.begin(), curves.end());
// Print the size of the arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
It is also possible to construct x-monotone curve objects, which represent x-monotone circular arcs or line segments, using similar constructors. Construction from a full circle is obviously not supported. See the Reference Manual for more details.
The traits class-template Arr_circular_line_arc_traits_2<CircularKernel> offered by the arrangement package also handles circular arcs and line segments. It is an alternative to the Arr_circle_segment_traits_2<Kernel> class-template. These two class templates, while serve similar purposes, are based on different concepts, and posses different characteristics. You are encouraged to experiment with both, compare their performance, and use the most suitable for your case.
31.6.5 A Traits Class for Conic Arcs
A conic curve is an algebraic curve of degree 2. Namely, it is the locus of all points (x,y) satisfying the equation C: r x2 + s y2 + t xy + u x + v y + w = 0, where the six coefficients ⟨r, s, t, u, v, w ⟩ completely characterize the curve. The sign of the expression ΔC = 4 r s - t2 determines the type of curve:
- If ΔC > 0 the curve is an ellipse. A circle is a special case of an ellipse, where r = s and t = 0.
- If ΔC = 0 the curve is a parabola - an unbounded conic curve with a single connected branch. When r = s = t = 0 we have a line, which can be considered as a degenerate parabola.
- If ΔC < 0 the curve is a hyperbola. That is, it is comprised of two disconnected unbounded branches.
As the arrangement package is suitable for bounded curves, we consider bounded segments of conic curves, referred to as conic arcs. A conic arc a may be either (i) a full ellipse, or (ii) defined by the tuple ⟨C, ps, pt, o ⟩, where C is a conic curve and ps and pt are two points on C (namely C(ps) = C(pt) = 0) that define the source and target of the arc, respectively. The arc is formed by traversing C from the source to the target going in the orientation specified by o, which is typically clockwise or counterclockwise orientation (but may also be collinear in case of degenerate conic curves).
We always assume that the conic coefficients ⟨r, s, t, u, v, w ⟩ are rational. When dealing with linear curves (line segments and polylines), similar assumptions guarantee that all intersection points also have rational coordinates, such that the arrangement of such curves can be constructed and maintained using only rational arithmetic. Unfortunately, this does not hold for conic curves, as the coordinates of intersection points of two conic curves with rational coefficients are in general algebraic numbers of degree 4.17 In addition, conic arcs may not necessarily be x-monotone, and must be split at points where the tangent to the arc is vertical. In the general case, such points typically have coordinates that are algebraic numbers of degree 2. It is therefore clear that we have to use different number types to represent the conic coefficients and the point coordinates. Note that as arrangement vertices induced by intersection points and points with vertical tangents are likely to have algebraic coordinates, we also allow the original endpoints of the input arcs ps and pt to have algebraic coordinates.
The Arr_conic_traits_2<RatKernel, AlgKernel, NtTraits> class template is designed for efficient handling of arrangements of bounded conic arcs. The template has three parameters, defined as follows:
- The RatKernel class is a geometric kernel, whose field type is an exact rational type. It is used to define basic geometric entities (e.g., a line segment or a circle) with rational coefficients. Typically we use one of the standard Cgal kernels, instantiated with the number type NtTraits::Rational (see below).
- The AlgKernel class is a geometric kernel whose field type is an exact algebraic type. It is used to define points with algebraic coordinates. Typically we use one of the standard Cgal kernels, instantiated with the number type NtTraits::Algebraic (see below).
- The NtTraits class (the number-type traits class) encapsulates all the numeric operations needed for performing the geometric computation carried out by the geometric traits class. It defines the Integer, Rational and Algebraic number-types, and supports several operations on these types, such as conversion between number types, solving quadratic equations and extracting the real roots of a polynomial with integer coefficients. It is highly recommended to use the CORE_algebraic_number_traits class, which is included in the arrangement package. It relies on the exact number types implemented in the Core library and performs exact computations on the number types it defines.
The Arr_conic_traits_2 models the ArrangementTraits_2 and ArrangementLandmarkTraits_2 concepts. (It supports the landmark point-location strategy). Its Point_2 type is derived from AlgKernel::Point_2, while the Curve_2 type represents a bounded, not necessarily x-monotone, conic arc. The X_monotone_curve_2 type is derived from Curve_2, but its constructors are to be used only by the traits class. You should therefore construct only Curve_2 objects and insert them into the arrangement using the insert() or insert() functions.
Conic arcs can be constructed from full ellipses or by specifying a supporting curve, two endpoints and an orientation. However, several constructors of Curve_2 are available to allow for some special cases, such as circular arcs or line segments. The Curve_2 (and the derived X_monotone_curve_2) classes also support basic access functions such as source(), target() and orientation().
Examples for Arrangements of Conics
The following example demonstrates the usage of the various constructors for conic arcs. The resulting arrangement is depicted in Figure 31.15. Especially noteworthy are the constructor of a circular arc that accepts three points and the constructor that allows specifying approximate endpoints, where the exact endpoints are given explicitly as intersections of the supporting conic with two other conic curves. Also note that as the preconditions required by some of these constructors are rather complicated (see the Reference Manual for the details), a precondition violation does not cause the program to terminate - instead, an invalid arc is created. We can verify the validity of an arc by using the is_valid() method. Needless to say, inserting invalid arcs into an arrangement is not allowed.
File: examples/Arrangement_on_surface_2/conics.cpp
#include <CGAL/basic.h>
#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
std::cout << "Sorry, this example needs CORE ..." << std::endl;
return 0;
}
#else
#include <CGAL/Cartesian.h>
#include <CGAL/CORE_algebraic_number_traits.h>
#include <CGAL/Arr_conic_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::CORE_algebraic_number_traits Nt_traits;
typedef Nt_traits::Rational Rational;
typedef Nt_traits::Algebraic Algebraic;
typedef CGAL::Cartesian<Rational> Rat_kernel;
typedef Rat_kernel::Point_2 Rat_point_2;
typedef Rat_kernel::Segment_2 Rat_segment_2;
typedef Rat_kernel::Circle_2 Rat_circle_2;
typedef CGAL::Cartesian<Algebraic> Alg_kernel;
typedef CGAL::Arr_conic_traits_2<Rat_kernel, Alg_kernel, Nt_traits>
Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Conic_arc_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
Arrangement_2 arr;
// Insert a hyperbolic arc, supported by the hyperbola y = 1/x
// (or: xy - 1 = 0) with the endpoints (1/5, 4) and (2, 1/2).
// Note that the arc is counterclockwise oriented.
Point_2 ps1 (Rational(1,4), 4);
Point_2 pt1 (2, Rational(1,2));
Conic_arc_2 c1 (0, 0, 1, 0, 0, -1, CGAL::COUNTERCLOCKWISE, ps1, pt1);
insert (arr, c1);
// Insert a full ellipse, which is (x/4)^2 + (y/2)^2 = 0 rotated by
// phi=36.87 degree (such that sin(phi) = 0.6, cos(phi) = 0.8),
// yielding: 58x^2 + 72y^2 - 48xy - 360 = 0.
Conic_arc_2 c2 (58, 72, -48, 0, 0, -360);
insert (arr, c2);
// Insert the segment (1, 1) -- (0, -3).
Rat_point_2 ps3 (1, 1);
Rat_point_2 pt3 (0, -3);
Conic_arc_2 c3 (Rat_segment_2 (ps3, pt3));
insert (arr, c3);
// Insert a circular arc supported by the circle x^2 + y^2 = 5^2,
// with (-3, 4) and (4, 3) as its endpoints. We want the arc to be
// clockwise oriented, so it passes through (0, 5) as well.
Rat_point_2 ps4 (-3, 4);
Rat_point_2 pm4 (0, 5);
Rat_point_2 pt4 (4, 3);
Conic_arc_2 c4 (ps4, pm4, pt4);
CGAL_assertion (c4.is_valid());
insert (arr, c4);
// Insert a full unit circle that is centered at (0, 4).
Rat_circle_2 circ5 (Rat_point_2(0,4), 1);
Conic_arc_2 c5 (circ5);
insert (arr, c5);
// Insert a parabolic arc that is supported by a parabola y = -x^2
// (or: x^2 + y = 0) and whose endpoints are (-sqrt(3), -3) ~ (-1.73, -3)
// and (sqrt(2), -2) ~ (1.41, -2). Notice that since the x-coordinates
// of the endpoints cannot be acccurately represented, we specify them
// as the intersections of the parabola with the lines y = -3 and y = -2.
// Note that the arc is clockwise oriented.
Conic_arc_2 c6 =
Conic_arc_2 (1, 0, 0, 0, 1, 0, // The parabola.
CGAL::CLOCKWISE,
Point_2 (-1.73, -3), // Approximation of the source.
0, 0, 0, 0, 1, 3, // The line: y = -3.
Point_2 (1.41, -2), // Approximation of the target.
0, 0, 0, 0, 1, 2); // The line: y = -2.
CGAL_assertion (c6.is_valid());
insert (arr, c6);
// Insert the right half of the circle centered at (4, 2.5) whose radius
// is 1/2 (therefore its squared radius is 1/4).
Rat_circle_2 circ7 (Rat_point_2(4, Rational(5,2)), Rational(1,4));
Point_2 ps7 (4, 3);
Point_2 pt7 (4, 2);
Conic_arc_2 c7 (circ7, CGAL::CLOCKWISE, ps7, pt7);
insert (arr, c7);
// Print out the size of the resulting arrangement.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
#endif
The last example in this section demonstrates how the conic-traits class can handle intersection points with multiplicity. The supporting curves of the two arcs, a circle centered at (0,(1)/(2)) with radius (1)/(2), and the hyperbola y = (x2)/(1-x),18 intersect at the origin such that the intersection point has multiplicity 3 (note that they both have the same horizontal tangent at (0,0) and the same curvature 1). In addition, they have another intersection point at ((1)/(2),(1)/(2)) of multiplicity 1:
File: examples/Arrangement_on_surface_2/conic_multiplicities.cpp
#include <CGAL/basic.h>
#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
std::cout << "Sorry, this example needs CORE ..." << std::endl;
return 0;
}
#else
#include <CGAL/Cartesian.h>
#include <CGAL/CORE_algebraic_number_traits.h>
#include <CGAL/Arr_conic_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_naive_point_location.h>
#include "arr_print.h"
typedef CGAL::CORE_algebraic_number_traits Nt_traits;
typedef Nt_traits::Rational Rational;
typedef Nt_traits::Algebraic Algebraic;
typedef CGAL::Cartesian<Rational> Rat_kernel;
typedef Rat_kernel::Point_2 Rat_point_2;
typedef Rat_kernel::Segment_2 Rat_segment_2;
typedef Rat_kernel::Circle_2 Rat_circle_2;
typedef CGAL::Cartesian<Algebraic> Alg_kernel;
typedef CGAL::Arr_conic_traits_2<Rat_kernel,
Alg_kernel,
Nt_traits> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Conic_arc_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_naive_point_location<Arrangement_2> Naive_pl;
int main ()
{
Arrangement_2 arr;
Naive_pl pl (arr);
// Insert a hyperbolic arc, supported by the hyperbola y = x^2/(1-x)
// (or: x^2 + xy - y = 0) with the endpoints (-1, 1/2) and (1/2, 1/2).
// Note that the arc is counterclockwise oriented.
Point_2 ps1 (-1, Rational(1,2));
Point_2 pt1 (Rational(1,2), Rational(1,2));
Conic_arc_2 cv1 (1, 0, 1, 0, -1, 0, CGAL::COUNTERCLOCKWISE, ps1, pt1);
insert (arr, cv1, pl);
// Insert the bottom half of the circle centered at (0, 1/2) whose radius
// is 1/2 (therefore its squared radius is 1/4).
Rat_circle_2 circ2 (Rat_point_2(0, Rational(1,2)), Rational(1,4));
Point_2 ps2 (-Rational(1,2), Rational(1,2));
Point_2 pt2 (Rational(1,2), Rational(1,2));
Conic_arc_2 cv2 (circ2, CGAL::COUNTERCLOCKWISE, ps2, pt2);
insert (arr, cv2, pl);
// Print the resulting arrangement.
print_arrangement (arr);
return 0;
}
#endif
31.6.6 A Traits Class for Arcs of Rational Functions
The traits class Arr_rational_function_traits_2<AlgebraicKernel_d_1> handles bounded and unbounded arcs of rational functions, referred to as rational arcs (in particular, such an arc may correspond to the entire graph of a rational function), and enables the construction and maintenance of arrangements of such arcs. Rational functions, and polynomial functions in particular, are not only interesting in their own right, they are also very useful for approximating or interpolating more complicated curves; see, e.g., [PTVF02, Chapter 3].
Arr_rational_function_traits_2<AlgebraicKernel_d_1> is a model of the concepts ArrangementTraits_2, ArrangementOpenBoundaryTraits_2, and ArrangementDirectionalXMonotoneTraits_2; the later enables Boolean set operations. Note that it is not a model of ArrangementLandmarkTraits_2 concept, so it is impossible to use the landmark point-location strategy with this traits class.
A rational function y = (P(x))/(Q(x)) is defined by two polynomials P and Q of arbitrary degrees. If Q(x) = 1 then the function is a simple polynomial function. Usually the domain is ℝ but the function may also be restricted to a bounded interval [xmin, xmax] or defined over a ray (-∞, xmax] or [xmin, ∞). Rational functions are represented by the nested type Curve_2. A rational arc is always x-monotone in the mathematical sense. However, it is not necessarily continuous, as it may have singularities. An arc that has singularities must be split into continuous portions before being inserted into the arrangement. Arbitrary rational functions are represented by the nested type Curve_2 and continuous portions of rational functions are represented by the nested type X_monotone_curve_2. Constructors for both types are provided by the traits. A Curve_2 may be split up into several X_monotone_curve_2 using Make_x_monotone_2.
Using the Arr_rational_function_traits_2<AlgebraicKernel_d_1> class template it is possible to construct and maintain arrangement of rational arcs. The template parameter of the traits must be a model of the concept AlgebraicKernel_d_1. A rational function is represented as the quotient of two polynomials P and Q of type AlgebraicKernel_d_1::Polynomial_1 and an x-interval over which the polynomials are defined. The type of the polynomial coefficients, namely AlgebraicKernel_d_1::Coefficient, cannot be algebraic. Moreover, it is recommended that this type is not made rational either, since using rational, as opposed to integral, coefficients does not extend the range of the rational arcs and is typically less efficient. The type of the interval bounds, namely AlgebraicKernel_d_1::Bound, however, can be algebraic. A point is represented by a rational function and its x-coordinate, which is of type AlgebraicKernel_d_1::Algebraic_real_1. Note that an explicit representation of the y-coordinate is only computed upon request, as it can be a rather costly operation.
The constructed rational functions are cached by the traits class. The cache is local to each traits class object. It is therefore necessary to construct curves using only the constructor objects provided by member functions of the traits class. Moreover, a curve must only be used by the traits class object that was used to construct it. The cache is automatically cleaned up from time to time. The amortized clean up costs are constant. In addition, there is also a separate member function that cleans up the cache on demand.
The curve constructors have an additional advantage. They conveniently enable the provision of two polynomials that define a rational arc using rational coefficients. For example, let P and Q denote two polynomials with integral coefficients that define a rational arc at interest, and let P' and Q' denote two polynomials with rational coefficients that define the same rational arc; that is, the quotients P/Q and P'/Q' are identical. You can construct the rational arc providing the coefficients of P' and Q' to the constructor. In this case the constructor normalizes the coefficients and stores the desired polynomials P and Q.
The following example demonstrates the construction of an arrangement of rational arcs depicted in Figure 31.16. Note the usage of the two constructors, for polynomial arcs and for rational arcs:
File: examples/Arrangement_on_surface_2/rational_functions.cpp
#include <CGAL/basic.h>
#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
std::cout << "Sorry, this example needs CORE ..." << std::endl;
return 0;
}
#else
#include <CGAL/CORE_BigInt.h> // NT
#include <CGAL/Algebraic_kernel_d_1.h> // Algebraic Kernel
#include <CGAL/Arr_rational_function_traits_2.h> // Traits
#include <CGAL/Arrangement_2.h> // Arrangement
typedef CORE::BigInt Number_type;
typedef CGAL::Algebraic_kernel_d_1<Number_type> AK1;
typedef CGAL::Arr_rational_function_traits_2<AK1> Traits_2;
typedef Traits_2::Polynomial_1 Polynomial_1;
typedef Traits_2::Algebraic_real_1 Alg_real_1;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
CGAL::set_pretty_mode(std::cout); // for nice printouts.
// create a polynomial representing x .-)
Polynomial_1 x = CGAL::shift(Polynomial_1(1),1);
// Traits class object
Traits_2 traits;
Traits_2::Construct_x_monotone_curve_2 construct_arc
= traits.construct_x_monotone_curve_2_object();
// container storing all arcs
std::vector<Traits_2::X_monotone_curve_2> arcs;
// Create an arc supported by the polynomial y = x^4 - 6x^2 + 8,
// defined over the interval [-2.1, 2.1]:
Polynomial_1 P1 = x*x*x*x - 6*x*x + 8;
Alg_real_1 l(Traits_2::Algebraic_kernel_d_1::Bound(-2.1));
Alg_real_1 r(Traits_2::Algebraic_kernel_d_1::Bound(2.1));
arcs.push_back(construct_arc(P1, l, r));
// Create an arc supported by the function y = x / (1 + x^2),
// defined over the interval [-3, 3]:
Polynomial_1 P2 = x;
Polynomial_1 Q2 = 1+x*x;
arcs.push_back(construct_arc(P2, Q2, Alg_real_1(-3), Alg_real_1(3)));
// Create an arc supported by the parbola y = 8 - x^2,
// defined over the interval [-2, 3]:
Polynomial_1 P3 = 8 - x*x;
arcs.push_back(construct_arc(P3, Alg_real_1(-2), Alg_real_1(3)));
// Create an arc supported by the line y = -2x,
// defined over the interval [-3, 0]:
Polynomial_1 P4 = -2*x;
arcs.push_back(construct_arc(P4, Alg_real_1(-3), Alg_real_1(0)));
// Construct the arrangement of the four arcs.
// Print the arcs.
for (unsigned int i(0); i < arcs.size(); ++i)
std::cout << arcs[i]<<std::endl;
Arrangement_2 arr(&traits);
insert(arr, arcs.begin(), arcs.end());
// Print the arrangement size.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
#endif
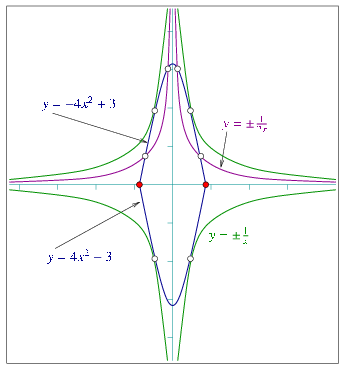
The following example demonstrates the construction of an arrangement of six rational arcs - four unbounded arcs and two bounded ones - as depicted in Figure 31.17. Note the usage of the constructors of an entire rational function and of an infinite ``ray'' of such a function. Also observe that the hyperbolas y = ± (1)/(x) and y = ± (1)/(2x) never intersect, although they have common vertical and horizontal asymptotes, so very ``thin'' unbounded faces are created between them:
File: examples/Arrangement_on_surface_2/unbounded_rational_functions.cpp
#include <CGAL/basic.h>
#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
std::cout << "Sorry, this example needs CORE ..." << std::endl;
return 0;
}
#else
#include <CGAL/CORE_BigInt.h> // NT
#include <CGAL/Algebraic_kernel_d_1.h> // Algebraic Kernel
#include <CGAL/Arr_rational_function_traits_2.h> // Traits
#include <CGAL/Arrangement_2.h> // Arrangement
typedef CORE::BigInt Number_type;
typedef CGAL::Algebraic_kernel_d_1<Number_type> AK1;
typedef CGAL::Arr_rational_function_traits_2<AK1> Traits_2;
typedef Traits_2::Polynomial_1 Polynomial_1;
typedef Traits_2::Algebraic_real_1 Alg_real_1;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
CGAL::set_pretty_mode(std::cout); // for nice printouts.
// Traits class object
AK1 ak1;
Traits_2 traits(&ak1);
// constructor for rational functions
Traits_2::Construct_curve_2 construct = traits.construct_curve_2_object();
// a polynomial representing x .-)
Polynomial_1 x = CGAL::shift(Polynomial_1(1),1);
// container storing all arcs
std::vector<Traits_2::Curve_2> arcs;
// Create the rational functions (y = 1 / x), and (y = -1 / x).
Polynomial_1 P1(1);
Polynomial_1 minusP1(-P1);
Polynomial_1 Q1 = x;
arcs.push_back(construct(P1, Q1));
arcs.push_back(construct(minusP1, Q1));
// Create a bounded segments of the parabolas (y = -4*x^2 + 3) and
// (y = 4*x^2 - 3), defined over [-sqrt(3)/2, sqrt(3)/2].
Polynomial_1 P2 = -4*x*x+3;
Polynomial_1 minusP2 = -P2;
std::vector<std::pair<Alg_real_1,int> > roots;
// [-sqrt(3)/2, sqrt(3)/2]
traits.algebraic_kernel_d_1()->solve_1_object()(P2, std::back_inserter(roots));
arcs.push_back(construct(P2, roots[0].first, roots[1].first));
arcs.push_back(construct(minusP2, roots[0].first, roots[1].first));
// Create the rational function (y = 1 / 2*x) for x > 0, and the
// rational function (y = -1 / 2*x) for x < 0.
Polynomial_1 P3(1);
Polynomial_1 minusP3(-P3);
Polynomial_1 Q3 = 2*x;
arcs.push_back(construct(P3, Q3, Alg_real_1(0), true));
arcs.push_back(construct(minusP3, Q3, Alg_real_1(0), false));
// Construct the arrangement of the six arcs.
//Arrangement_2 arr(&traits);
Arrangement_2 arr;
insert(arr, arcs.begin(), arcs.end());
// Print the arrangement size.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< " (plus " << arr.number_of_vertices_at_infinity()
<< " at infinity)"
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces()
<< " (" << arr.number_of_unbounded_faces() << " unbounded)"
<< std::endl << std::endl;
return 0;
}
#endif
31.6.7 A Traits Class for Planar Bézier Curves
A planar Bézier curve B is a parametric curve defined by a sequence of control points p0, … , pn as follows:
|
Using the Arr_Bezier_curve_traits_2<RatKernel, AlgKernel, NtTraits> class template it is possible to construct and maintain arrangements of Bézier curves that are given by rational control points (a sequence of objects of the RatKernel::Point_2 type). We can handle curves of arbitrary degree (in general, a sequence of n+1 control points define a Bézier curve of degree n). The template parameters are the same ones used by the Arr_conic_traits_2 class template, and here it is also recommended to use the CORE_algebraic_number_traits class, with Cartesian kernels instantiated with the Rational and Algebraic number-types defined by this class.
As mentioned above, we assume that the coordinates of all control points that define a Bézier curve are rational numbers, so both X(t) and Y(t) are polynomials with rational coefficients. The intersection points between curves are however algebraic numbers, and their exact computation is time-consuming. The traits class therefore contains a layer of geometric filtering that performs all computation in an approximate manner whenever possible. Thus, it resorts to exact computations only when the approximate computation fails to produce an unambiguous result. Note that most arrangement vertices are therefore associated with approximated points. You cannot access the coordinates of such points and obtain them as algebraic numbers, and only access to the approximate coordinates in possible. See the Reference Manual for the exact interface of the Point_2, Curve_2 and X_monotone_curve_2 defined by the traits class.
The Arr_Bezier_curve_traits_2 is a model of the ArrangementTraits_2 concept (but not of the ArrangementLandmarkTraits_2 concept, so it is impossible to use the landmark point-location strategy for arrangements of rational arcs).

The following example reads a set of Bézier curves from an input file, where each file is specified by an integer stating its number of control points, followed by the sequence of control points, given in integer or rational coordinates. By default, the program uses the Bezier.dat file, which contains ten curves of degree 5 each; their resulting arrangement is depicted in Figure 31.18.
File: examples/Arrangement_on_surface_2/Bezier_curves.cpp
#include <CGAL/basic.h>
#ifndef CGAL_USE_CORE
#include <iostream>
int main ()
{
std::cout << "Sorry, this example needs CORE ..." << std::endl;
return 0;
}
#else
#include <CGAL/Cartesian.h>
#include <CGAL/CORE_algebraic_number_traits.h>
#include <CGAL/Arr_Bezier_curve_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::CORE_algebraic_number_traits Nt_traits;
typedef Nt_traits::Rational NT;
typedef Nt_traits::Rational Rational;
typedef Nt_traits::Algebraic Algebraic;
typedef CGAL::Cartesian<Rational> Rat_kernel;
typedef CGAL::Cartesian<Algebraic> Alg_kernel;
typedef Rat_kernel::Point_2 Rat_point_2;
typedef CGAL::Arr_Bezier_curve_traits_2<Rat_kernel, Alg_kernel, Nt_traits>
Traits_2;
typedef Traits_2::Curve_2 Bezier_curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main (int argc, char *argv[])
{
// Get the name of the input file from the command line, or use the default
// Bezier.dat file if no command-line parameters are given.
const char *filename = (argc > 1) ? argv[1] : "Bezier.dat";
// Open the input file.
std::ifstream in_file (filename);
if (! in_file.is_open()) {
std::cerr << "Failed to open " << filename << std::endl;
return 1;
}
// Read the curves from the input file.
unsigned int n_curves;
std::list<Bezier_curve_2> curves;
Bezier_curve_2 B;
unsigned int k;
in_file >> n_curves;
for (k = 0; k < n_curves; k++) {
// Read the current curve (specified by its control points).
in_file >> B;
curves.push_back (B);
std::cout << "B = {" << B << "}" << std::endl;
}
// Construct the arrangement.
Arrangement_2 arr;
insert (arr, curves.begin(), curves.end());
// Print the arrangement size.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
#endif
31.6.8 A Traits Class for Planar Algebraic Curves of Arbitrary Degree
An algebraic curve C in the plane is defined as the (real) zero locus of a polynomial f(x,y) in two variables. The curve is uniquely defined by f (although several polynomials might define the same curve). We call f a defining polynomial of C.
We consider arrangements induced by algebraic curves or by (weakly) x-monotone segments for algebraic curves (Such a segment is not necessarily the maximal possible (weakly) x-monotone segment; see below.) When talking about algebraic curves, we use the term ``segment'' for a continuous, possibly non-linear subset of an algebraic curve - see the definition below. There are no restrictions on the algebraic curve, that means, we support unbounded curves, vertical curves or segments, and isolated points.
The Arr_algebraic_segment_traits_2<Coefficient> class template is a model of the ArrangementTraits_2 concept (but not of the ArrangementLandmarkTraits_2 concept, so it is impossible to use the landmark point-location strategy for arrangements of algebraic curves). The template argument Coefficient determines the type of the scalar coefficients of the polynomial. Currently supported types are leda_integer, CORE::BigInt, and any instance of CGAL::Sqrt_extension<A,B> instantiated with one of the integral types above.
The traits class defines a type Curve_2 for algebraic curves. Such a type can be constructed by the Construct_curve_2 functor, which accepts an instance of Polynomial_2 as an argument. This polynomial type is also available by the traits class and constitutes a valid model of the concept Polynomial_d with two variables (see ??).
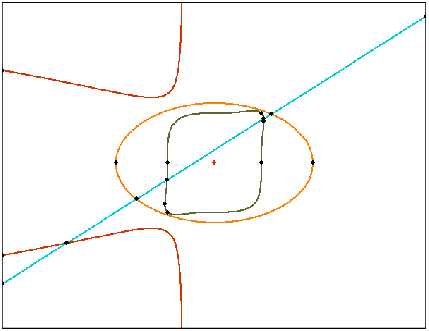
The following examples computes the arrangement induced by the four curves in Figure 31.19
File: examples/Arrangement_on_surface_2/algebraic_curves.cpp
#include <CGAL/basic.h>
#include <iostream>
#if (!CGAL_USE_CORE) && (!CGAL_USE_LEDA) && (!(CGAL_USE_GMP && CGAL_USE_MPFI))
int main ()
{
std::cout << "Sorry, this example needs CORE, LEDA, or GMP+MPFI ..."
<< std::endl;
return 0;
}
#else
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_algebraic_segment_traits_2.h>
#if CGAL_USE_GMP && CGAL_USE_MPFI
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz Integer;
#elif CGAL_USE_CORE
#include <CGAL/CORE_BigInt.h>
typedef CORE::BigInt Integer;
#else
#include <CGAL/leda_integer.h>
typedef LEDA::integer Integer;
#endif
typedef CGAL::Arr_algebraic_segment_traits_2<Integer> Arr_traits_2;
typedef CGAL::Arrangement_2<Arr_traits_2> Arrangement_2;
typedef Arr_traits_2::Curve_2 Curve_2;
typedef Arr_traits_2::Polynomial_2 Polynomial_2;
int main() {
// For nice printouts
CGAL::set_pretty_mode(std::cout);
Arr_traits_2 arr_traits;
// Functor to create a curve from a Polynomial_2
Arr_traits_2::Construct_curve_2 construct_curve
= arr_traits.construct_curve_2_object();
Polynomial_2 x = CGAL::shift(Polynomial_2(1),1,0);
Polynomial_2 y = CGAL::shift(Polynomial_2(1),1,1);
Arrangement_2 arr(&arr_traits);
// Construct an (unbounded line) with equation 3x-5y+2=0
Polynomial_2 f1 = 3*x-5*y+2;
Curve_2 cv1 = construct_curve(f1);
std::cout << "Adding curve " << f1 << " to the arrangement" << std::endl;
CGAL::insert(arr,cv1);
// Construct the ellipse x^2+3*y^2-10=0
Polynomial_2 f2 = CGAL::ipower(x,2)+3*CGAL::ipower(y,2)-10;
Curve_2 cv2 = construct_curve(f2);
std::cout << "Adding curve " << f2 << " to the arrangement" << std::endl;
CGAL::insert(arr,cv2);
// Construct a cubic curve with isoated point, and vertical asymptote
// x^2+y^2+xy^2
Polynomial_2 f3 = CGAL::ipower(x,2)+CGAL::ipower(y,2)+x*CGAL::ipower(y,2);
Curve_2 cv3 = construct_curve(f3);
std::cout << "Adding curve " << f3 << " to the arrangement" << std::endl;
CGAL::insert(arr,cv3);
// Construct a curve of degree 6 with equation x^6+y^6-x^3y^3-12
Polynomial_2 f4 = CGAL::ipower(x,6)+CGAL::ipower(y,6)-
CGAL::ipower(x,3)*CGAL::ipower(y,3)-12;
Curve_2 cv4 = construct_curve(f4);
std::cout << "Adding curve " << f4 << " to the arrangement" << std::endl;
CGAL::insert(arr,cv4);
// Print the arrangement size.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
#endif
We first give a precise definition of segments of algebraic curves. A point p on a curve Cf ⊂ ℝ2 (with f its defining equation) is called semi-regular, if locally around p, Cf can be written as a function graph of some continuous function in x or in y (we also say that p is parameterizable in x or y, respectively). The only two cases of non-semi-regular points are isolated points, and self-intersections. A segment of a curve is a closed and continuous point set such that each interior point is semi-regular. It follows that a weakly x-monotone segment is either a completely vertical segment, or a segment whose interior points are all parameterizable in x.
The traits class allows to construct weakly x-monotone segments of a curve using the Construct_x_monotone_segment_2 functor. The X_monotone_curve_2 type of the traits class represents weakly x-monotone segments of a curve; however, segments may need to be further subdivided into several (sub-)segments, for technical reasons. Therefore, Construct_x_monotone_segment_2 constructs a sequence of X_monotone_curve_2 objects, whose union represents the weakly x-monotone segment that was queried. We call a segment terminal if it can be represented by the type X_monotone_curve_2.
| f(p)=0= |
| (p). |
Coordinates of points are represented by the type Algebraic_real_1, which is defined in the traits class. This type is taken from a model of the AlgebraicKernel_1 concept, which is also available by the type Algebraic_kernel_1. One can use this model to create algebraic numbers as roots of univariate polynomials, and process them, for instance, compare them, or approximate them to any precision. See the documentation of AlgebraicKernel_1 for more information. One can construct an object of type Point_2 by a triple (x0,cv,i), which means that the i-th point (counted from below) in the fiber of cv at the x-coordinate x0 is constructed. This is also how points are presented internally. In the example displayed in Figure 31.20, if x1 denotes the x-coordinate of p, and cv represents the algebraic curve, then p could be represented by (x1,cv,3). If x2 is the x-coordinate of q, then (x2,cv,1) is a valid representation of q. Although the y-coordinate of an object of type Point_2 can be queried, we recommend to be careful with that option, since computing an explicit representation of the y-coordinate as an Algebraic_real_1 object can become rather expensive.
The following code exemplifies various methods to construct algebraic segments. The computed arrangement is displayed in Figure 31.21.
File: examples/Arrangement_on_surface_2/algebraic_segments.cpp
#include <CGAL/basic.h>
#include <iostream>
#if (!CGAL_USE_CORE) && (!CGAL_USE_LEDA) && (!(CGAL_USE_GMP && CGAL_USE_MPFI))
int main ()
{
std::cout << "Sorry, this example needs CORE, LEDA, or GMP+MPFI ..."
<< std::endl;
return 0;
}
#else
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_algebraic_segment_traits_2.h>
#if CGAL_USE_GMP && CGAL_USE_MPFI
#include <CGAL/Gmpz.h>
typedef CGAL::Gmpz Integer;
#elif CGAL_USE_CORE
#include <CGAL/CORE_BigInt.h>
typedef CORE::BigInt Integer;
#else
#include <CGAL/leda_integer.h>
typedef LEDA::integer Integer;
#endif
typedef CGAL::Arr_algebraic_segment_traits_2<Integer> Arr_traits_2;
typedef CGAL::Arrangement_2<Arr_traits_2> Arrangement_2;
typedef Arr_traits_2::Curve_2 Curve_2;
typedef Arr_traits_2::Polynomial_2 Polynomial_2;
typedef Arr_traits_2::Algebraic_real_1 Algebraic_real_1;
typedef Arr_traits_2::X_monotone_curve_2 X_monotone_curve_2;
typedef Arr_traits_2::Point_2 Point_2;
int main() {
Arr_traits_2 arr_traits;
Arr_traits_2::Construct_curve_2 construct_curve
= arr_traits.construct_curve_2_object();
Arr_traits_2::Construct_x_monotone_segment_2 construct_x_monotone_segment
= arr_traits.construct_x_monotone_segment_2_object();
Arr_traits_2::Construct_point_2 construct_point
= arr_traits.construct_point_2_object();
Arr_traits_2::Make_x_monotone_2 make_x_monotone
= arr_traits.make_x_monotone_2_object();
Arrangement_2 arr(&arr_traits);
std::vector<X_monotone_curve_2> segs;
Polynomial_2 x = CGAL::shift(Polynomial_2(1),1,0);
Polynomial_2 y = CGAL::shift(Polynomial_2(1),1,1);
// Construct x^4+y^3-1
Curve_2 cv0 = construct_curve(CGAL::ipower(x,4)+CGAL::ipower(y,3)-1);
// Construct all x-monotone segments using the Make_x_mononotone functor
std::vector<CGAL::Object> pre_segs;
make_x_monotone(cv0,std::back_inserter(pre_segs));
// Cast all CGAL::Objects into X_monotone_segment_2
// (the vector might also contain Point_2 objects for isolated points,
// but not for this instance
for(size_t i = 0; i < pre_segs.size(); i++ ) {
X_monotone_curve_2 curr;
bool check = CGAL::assign(curr,pre_segs[i]);
assert(check);
segs.push_back(curr);
}
// Construct an ellipse with equation 2*x^2+5*y^2-7=0
Curve_2 cv1 = construct_curve(2*CGAL::ipower(x,2)+5*CGAL::ipower(y,2)-7);
// Construct point on the upper arc (counting of arc numbers starts with 0!
Point_2 p11 = construct_point(Algebraic_real_1(0),cv1,1);
construct_x_monotone_segment(cv1,p11,Arr_traits_2::POINT_IN_INTERIOR,
std::back_inserter(segs));
// Construct a vertical cusp x^2-y^3=0
Curve_2 cv2 = construct_curve(CGAL::ipower(x,2)-CGAL::ipower(y,3));
// Construct a segment containing the cusp point.
// This adds to X_monotone_curve_2 objects to the vector,
// because the cusp is a critical point
Point_2 p21 = construct_point(Algebraic_real_1(-2),cv2,0);
Point_2 p22 = construct_point(Algebraic_real_1(2),cv2,0);
construct_x_monotone_segment(cv2,p21,p22,std::back_inserter(segs));
// Construct an unbounded curve, starting at x=3
Point_2 p23 = construct_point(Algebraic_real_1(3),cv2,0);
construct_x_monotone_segment(cv2,p23,Arr_traits_2::MIN_ENDPOINT,
std::back_inserter(segs));
// Construct another conic: y^2-x^2+1
Curve_2 cv3 = construct_curve(CGAL::ipower(y,2)-CGAL::ipower(x,2)+1);
Point_2 p31 = construct_point(Algebraic_real_1(2),cv3,1);
construct_x_monotone_segment(cv3,p31,Arr_traits_2::MAX_ENDPOINT,
std::back_inserter(segs));
// Construct a vertical segment
Point_2 v1 = construct_point(0,0);
Point_2 v2 = construct_point(Algebraic_real_1(0),cv1,1);
construct_x_monotone_segment(v1,v2,std::back_inserter(segs));
CGAL::insert(arr,segs.begin(),segs.end());
// Add some isolated points (must be wrapped into CGAL::Object)
std::vector<CGAL::Object> isolated_points;
isolated_points.push_back
(CGAL::make_object(construct_point(Algebraic_real_1(2),cv3,0)));
isolated_points.push_back
(CGAL::make_object(construct_point(Integer(1),Integer(5))));
isolated_points.push_back
(CGAL::make_object(construct_point(Algebraic_real_1(-1),
Algebraic_real_1(5))));
CGAL::insert(arr,isolated_points.begin(), isolated_points.end());
// Print the arrangement size.
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
#endif
31.6.9 Traits-Class Decorators
Geometric traits-class decorators allow you to attach auxiliary data to curves and to points. The data is automatically manipulated by the decorators and distributed to the constructed geometric entities. Note that additional information can alternatively be maintained by extending the vertex, halfedge, or face types provided by the Dcel class used by the arrangement; see the details in Section 31.8.
The arrangement package includes a generic traits-class decorator template named Arr_curve_data_traits_2<BaseTraits, XMonotoneCurveData, Merge, CurveData, Convert>. This decorator is used to attach a data field to curves and to x-monotone curves. It is parameterized by a base-traits class, which is one of the geometric traits classes described in the previous subsections, or a user-defined traits class. The curve-data decorator derives itself from the base-traits class, and in particular inherits its Point_2 type. In addition:
- Curve_2 is derived from the basic BaseTraits::Curve_2 class, extending it by an extra field of type CurveData.
- X_monotone_curve_2 is derived from the basic BaseTraits::X_monotone_curve_2 class, extending it by an extra field of type XMonotoneCurveData.
You can create an extended curve (or an extended x-monotone curve) from a basic curve and a curve-data object. When curves are inserted into an arrangement, they may be split, and the decorator handles their data fields automatically:
- When a curve is subdivided into x-monotone subcurves, its
data field of type CurveData is converted to an XMonotoneCurveData
object d using the Convert functor. The object d is automatically
associated with each of the resulting x-monotone subcurves.
Note that by default, the CurveData type is identical to the XMonotoneCurveData type (and the conversion functor Convert is trivially defined). Thus, the data field associated with the original curve is just duplicated and stored with the x-monotone subcurves.
- When an x-monotone curve is split into two, the decorator class automatically copies its data field to both resulting subcurves.
- When intersecting two x-monotone curves c1 and c2, the result may include overlapping sections, represented as x-monotone curves. In this case the data fields of c1 and c2 are merged into a single XMonotoneCurveData object, using the Merge functor, which is supplied as a parameter to the traits class-template. The resulting object is assigned to the data field of the overlapping subcurves.
- Merging two x-monotone curves is allowed only when (i) the two curves are geometrically mergeable - that is, the base-traits class allows to merge them - and (ii) the two curves store the same data field.
The Arr_consolidated_curve_data_traits_2<BaseTraits, Data> decorator specializes the generic curve-data decorator. It extends the basic BaseTraits::Curve_2 by a single Data field, and the basic BaseTraits::X_monotone_curve_2 with a set of (distinct) data objects. The Data type is required to support the equality operator, used to ensure that each set contains only distinct data objects with no duplicates. When a curve with a data field d is subdivided into x-monotone subcurves, each subcurve is associated with a set S = { d }. In case of an overlap between two x-monotone curves c1 and c2 with associated data sets S1 and S2, respectively, the overlapping subcurve is associated with the consolidated set S1 ∪ S2.
Examples
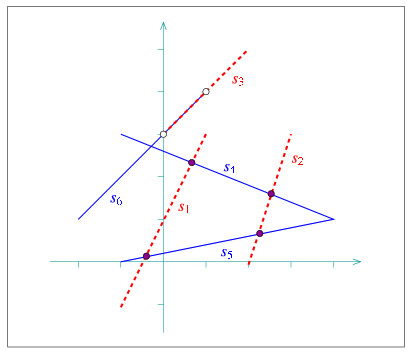
In the following example, we use Arr_segment_traits_2 as our base-traits class, attaching an additional color field to the segments using the consolidated curve-data traits class. A color may be either blue or red. Having constructed the arrangement of colored segments, as depicted in Figure 31.22, we detect the vertices that have incident edges mapped to both blue and red segments. Thus, they correspond to red-blue intersection points. We also locate the edge that corresponds to overlaps between red and blue line segments:
File: examples/Arrangement_on_surface_2/consolidated_curve_data.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_consolidated_curve_data_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_landmarks_point_location.h>
enum Segment_color {
RED,
BLUE
};
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Segment_traits_2;
typedef Segment_traits_2::Curve_2 Segment_2;
typedef CGAL::Arr_consolidated_curve_data_traits_2
<Segment_traits_2, Segment_color> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Colored_segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_landmarks_point_location<Arrangement_2> Landmarks_pl;
int main ()
{
// Construct an arrangement containing three RED line segments.
Arrangement_2 arr;
Landmarks_pl pl (arr);
Segment_2 s1 (Point_2(-1, -1), Point_2(1, 3));
Segment_2 s2 (Point_2(2, 0), Point_2(3, 3));
Segment_2 s3 (Point_2(0, 3), Point_2(2, 5));
insert (arr, Colored_segment_2 (s1, RED), pl);
insert (arr, Colored_segment_2 (s2, RED), pl);
insert (arr, Colored_segment_2 (s3, RED), pl);
// Insert three BLUE line segments.
Segment_2 s4 (Point_2(-1, 3), Point_2(4, 1));
Segment_2 s5 (Point_2(-1, 0), Point_2(4, 1));
Segment_2 s6 (Point_2(-2, 1), Point_2(1, 4));
insert (arr, Colored_segment_2 (s4, BLUE), pl);
insert (arr, Colored_segment_2 (s5, BLUE), pl);
insert (arr, Colored_segment_2 (s6, BLUE), pl);
// Go over all vertices and print just the ones corresponding to intersection
// points between RED segments and BLUE segments. Note that we skip endpoints
// of overlapping sections.
Arrangement_2::Vertex_const_iterator vit;
Segment_color color;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
// Go over the incident halfedges of the current vertex and examine their
// colors.
bool has_red = false;
bool has_blue = false;
Arrangement_2::Halfedge_around_vertex_const_circulator eit, first;
eit = first = vit->incident_halfedges();
do {
// Get the color of the current half-edge.
if (eit->curve().data().size() == 1) {
color = eit->curve().data().front();
if (color == RED)
has_red = true;
else if (color == BLUE)
has_blue = true;
}
++eit;
} while (eit != first);
// Print the vertex only if incident RED and BLUE edges were found.
if (has_red && has_blue)
{
std::cout << "Red-blue intersection at (" << vit->point() << ")"
<< std::endl;
}
}
// Locate the edges that correspond to a red-blue overlap.
Arrangement_2::Edge_iterator eit;
for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit)
{
// Go over the incident edges of the current vertex and examine their
// colors.
bool has_red = false;
bool has_blue = false;
Traits_2::Data_container::const_iterator dit;
for (dit = eit->curve().data().begin(); dit != eit->curve().data().end();
++dit)
{
if (*dit == RED)
has_red = true;
else if (*dit == BLUE)
has_blue = true;
}
// Print the edge only if it corresponds to a red-blue overlap.
if (has_red && has_blue)
std::cout << "Red-blue overlap at [" << eit->curve() << "]" << std::endl;
}
return 0;
}
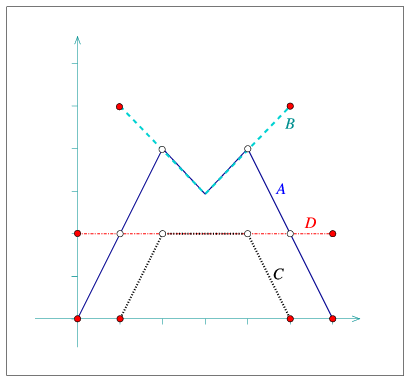
In the following example, we use Arr_polyline_traits_2 as our base-traits class, attaching an additional name field to each polyline using the generic curve-data traits class. In case of overlaps, we simply concatenate the names of the overlapping polylines. Also notice how we replace the curve associated with the edges that correspond to overlapping polylines with geometrically equivalent curves, but with a different data fields:
File: examples/Arrangement_on_surface_2/generic_curve_data.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_polyline_traits_2.h>
#include <CGAL/Arr_curve_data_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <string>
// Define a functor for concatenating name fields.
typedef std::string Name;
struct Merge_names
{
Name operator() (const Name& s1, const Name& s2) const
{
return (s1 + " " + s2);
}
};
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Segment_traits_2;
typedef CGAL::Arr_polyline_traits_2<Segment_traits_2> Polyline_traits_2;
typedef Polyline_traits_2::Curve_2 Polyline_2;
typedef CGAL::Arr_curve_data_traits_2<Polyline_traits_2, Name, Merge_names>
Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Curve_2;
typedef Traits_2::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
// Construct an arrangement of four polylines named A--D.
Arrangement_2 arr;
Point_2 points1[5] = {Point_2(0,0), Point_2(2,4), Point_2(3,3),
Point_2(4,4), Point_2(6,0)};
insert (arr, Curve_2 (Polyline_2 (points1, points1 + 5), "A"));
Point_2 points2[3] = {Point_2(1,5), Point_2(3,3), Point_2(5,5)};
insert (arr, Curve_2 (Polyline_2 (points2, points2 + 3), "B"));
Point_2 points3[4] = {Point_2(1,0), Point_2(2,2),
Point_2(4,2), Point_2(5,0)};
insert (arr, Curve_2 (Polyline_2 (points3, points3 + 4), "C"));
Point_2 points4[2] = {Point_2(0,2), Point_2(6,2)};
insert (arr, Curve_2 (Polyline_2 (points4, points4 + 2), "D"));
// Print all edges that correspond to an overlapping polyline.
Arrangement_2::Edge_iterator eit;
for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit) {
if (eit->curve().data().length() > 1) {
std::cout << "[" << eit->curve() << "] "
<< "named: " << eit->curve().data() << std::endl;
// Rename the curve associated with the edge.
arr.modify_edge (eit, X_monotone_curve_2 (eit->curve(), "overlap"));
}
}
return 0;
}
The third example we give in this section is based on dual_lines.cpp given in Section 31.5.2. It constructs the arrangement of the dual lines for a set of point given in an input file (by default we use coll_points.dat, which contains 50 points randomly selected on the grid [-100,100] × [-100,100]; the file contains two distinct triplets of collinear points). Here we use the generic curve-data decorator to attach the index of the primal point to each of the lines. Doing so, we can go over the incident edges of each vertex whose degree is greater than 4 and report the subsets collinear points (if we have a vertex of degree d, we actually need to go over (d)/(2) edges, as each incident line contributes exactly 2 edges). Note that in this case the dual line cannot overlap, so we use a dummy merge functor to instantiate the curve-data traits:
File: examples/Arrangement_on_surface_2/dual_with_data.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_linear_traits_2.h>
#include <CGAL/Arr_curve_data_traits_2.h>
#include <CGAL/Arrangement_2.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_linear_traits_2<Kernel> Linear_traits_2;
typedef Linear_traits_2::Point_2 Point_2;
typedef Linear_traits_2::Line_2 Line_2;
typedef CGAL::Arr_curve_data_traits_2<Linear_traits_2,
unsigned int> Traits_2;
typedef Traits_2::X_monotone_curve_2 X_monotone_curve_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main (int argc, char *argv[])
{
// Get the name of the input file from the command line, or use the default
// points.dat file if no command-line parameters are given.
const char * filename = (argc > 1) ? argv[1] : "coll_points.dat";
// Open the input file.
std::ifstream in_file (filename);
if (! in_file.is_open()) {
std::cerr << "Failed to open " << filename << " ..." << std::endl;
return (1);
}
// Read the points from the file, and consturct their dual lines.
std::vector<Point_2> points;
std::list<X_monotone_curve_2> dual_lines;
unsigned int n;
in_file >> n;
points.resize (n);
unsigned int k;
for (k = 0; k < n; ++k) {
int px, py;
in_file >> px >> py;
points[k] = Point_2 (px, py);
// The line dual to the point (p_x, p_y) is y = p_x*x - p_y,
// or: p_x*x - y - p_y = 0:
Line_2 dual_line = Line_2(Number_type(px),
Number_type(-1),
Number_type(-py));
// Generate the x-monotone curve based on the line and the point index.
dual_lines.push_back (X_monotone_curve_2 (dual_line, k));
}
in_file.close();
// Construct the dual arrangement by aggragately inserting the lines.
Arrangement_2 arr;
insert (arr, dual_lines.begin(), dual_lines.end());
// Look for vertices whose degree is greater than 4.
Arrangement_2::Vertex_const_iterator vit;
Arrangement_2::Halfedge_around_vertex_const_circulator circ;
unsigned int d;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) {
if (vit->degree() > 4) {
// There should be vit->degree()/2 lines intersecting at the current
// vertex. We print their primal points and their indices.
circ = vit->incident_halfedges();
for (d = 0; d < vit->degree() / 2; d++) {
k = circ->curve().data(); // The index of the primal point.
std::cout << "Point no. " << k+1 << ": (" << points[k] << "), ";
++circ;
}
std::cout << "are collinear." << std::endl;
}
}
return 0;
}
31.7 The Notification Mechanism
For some applications it is essential to know exactly what happens inside a specific arrangement-instance. For example, when a new curve is inserted into an arrangement, it might be desired to keep track of the faces that are split due to this insertion operation. Other important examples are the point-location strategies that require auxiliary data-structures (see Section 31.3.1), which must be notified on various local changes in the arrangement, in order to keep their data structures up-to-date. The arrangement package offers a mechanism that uses observers (see [GHJV95]) that can be attached to an arrangement instance and receive notifications about the changes this arrangement goes through.
The Arr_observer<Arrangement> class-template is parameterized with an arrangement class. It stores a pointer to an arrangement object, and is capable of receiving notifications just before a structural change occurs in the arrangement and immediately after such a change takes place. Arr_observer serves as a base class for other observer classes and defines a set of virtual notification functions, with default empty implementations.
The set of functions can be divided into three categories, as follows:
- Notifiers of changes that affect the entire topological structure
of the arrangement. This category consists of two pairs that
notify the observer of the following changes:
- The arrangement is cleared.
- The arrangement is assigned with the contents of another arrangement.
- Pairs of notifiers of a local change that occurs in the
topological structure. Most notifier functions belong to this
category. The relevant local changes include:
- A new vertex is constructed and associated with a point.
- An edge19 is constructed and associated with an x-monotone curve.
- An edge is split into two edges.
- An existing face is split into two faces, as a consequence of the insertion of a new edge.
- A hole is created in the interior of a face.
- Two holes are merged to form a single hole, as a consequence of the insertion of a new edge.
- A hole is moved from one face to another, as a consequence of a face split.
- Two edges are merged into one edge.
- Two faces are merged into one face, as a consequence of the removal of an edge that used to separate them.
- One hole is split into two, as a consequence of the deletion of an edge that used to connect the two components.
- A vertex is removed.
- An edge is removed.
- A hole is deleted from the interior of a face.
- Notifiers about a change applied by a free (global) function. This category consists of a single pair of notifiers, namely before_global_change() and after_global_change(). Neither of these functions is invoked by methods of the Arrangement_2 class. Instead, they are called by the free functions themselves. It is implied that no point-location queries (or any other queries for that matter) are issued between the calls to the notification functions above.
Each arrangement object stores a (possibly empty) list of pointers to Arr_observer objects, and whenever one of the structural changes listed in the first two categories above is about to take place, the arrangement object performs a forward traversal on this list and invokes the appropriate function of each observer. After the change takes place the observer list is traversed in a backward manner (from tail to head), and the appropriate notification function is invoked for each observer. This allows the nesting of observer objects.
Concrete arrangement-observer classes should inherit from Arr_observer. When an observer is constructed, it is attached to a valid arrangement supplied to the observed constructor, or alternatively the observer can be attached to the arrangement at a later time. When this happens, the observer instance inserts itself into the observer list of the associated arrangement and starts receiving notifications whenever this arrangement changes thereafter. Naturally, the observer object unregisters itself by removing itself from this list just before it is destroyed.
The trapezoidal RIC and the landmark point-location strategies both use observers to keep their auxiliary data structures up-to-date. Besides them, users can define their own observer classes, by inheriting from the base observer class and overriding the relevant notification functions, as required by their applications.
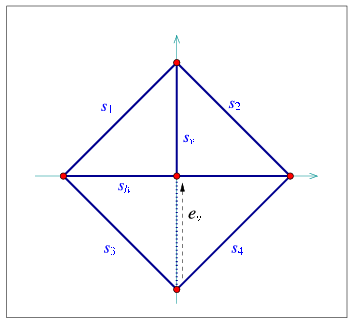
The following example shows how to define and use an observer class. The observer in the example keeps track of the arrangement faces, and prints a message whenever a face is split into two due to the insertion of an edge, and whenever two faces merge into one due to the removal of an edge. The layout of the arrangement is depicted in Figure 31.24:
File: examples/Arrangement_on_surface_2/observer.cpp
#include <CGAL/Cartesian.h>
#include <CGAL/Quotient.h>
#include <CGAL/MP_Float.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_observer.h>
typedef CGAL::Quotient<CGAL::MP_Float> Number_type;
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
// An arrangement observer, used to receive notifications of face splits and
// face mergers.
class My_observer : public CGAL::Arr_observer<Arrangement_2>
{
public:
My_observer (Arrangement_2& arr) :
CGAL::Arr_observer<Arrangement_2> (arr)
{}
virtual void before_split_face (Face_handle,
Halfedge_handle e)
{
std::cout << "-> The insertion of : [ " << e->curve()
<< " ] causes a face to split." << std::endl;
}
virtual void before_merge_face (Face_handle,
Face_handle,
Halfedge_handle e)
{
std::cout << "-> The removal of : [ " << e->curve()
<< " ] causes two faces to merge." << std::endl;
}
};
int main ()
{
// Construct the arrangement containing one diamond-shaped face.
Arrangement_2 arr;
My_observer obs (arr);
Segment_2 s1 (Point_2(-1, 0), Point_2(0, 1));
Segment_2 s2 (Point_2(0, 1), Point_2(1, 0));
Segment_2 s3 (Point_2(1, 0), Point_2(0, -1));
Segment_2 s4 (Point_2(0, -1), Point_2(-1, 0));
insert_non_intersecting_curve (arr, s1);
insert_non_intersecting_curve (arr, s2);
insert_non_intersecting_curve (arr, s3);
insert_non_intersecting_curve (arr, s4);
// Insert a vertical segment dividing the diamond into two, and a
// a horizontal segment further dividing the diamond into four:
Segment_2 s_vert (Point_2(0, -1), Point_2(0, 1));
Arrangement_2::Halfedge_handle
e_vert = insert_non_intersecting_curve (arr, s_vert);
Segment_2 s_horiz (Point_2(-1, 0), Point_2(1, 0));
insert (arr, s_horiz);
std::cout << "The initial arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Now remove a portion of the vertical segment.
remove_edge (arr, e_vert);
std::cout << "The final arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
Observers are especially useful when the Dcel records are extended and store additional data, as they help updating this data on-line. See Section 31.8 for more details and examples.
31.8 Extending the Dcel
For many applications of the arrangement package it is necessary to store additional information (perhaps of non-geometric nature) with the arrangement cells. As vertices are associated with Point_2 objects and edges (halfedge pairs) are associated with X_monotone_curve_2 objects, both defined by the traits class, it is possible to extend the traits-class type by using a traits-class decorator, as explained in Section 31.6.9, which may be a sufficient solution for some applications. However, the Dcel faces are not associated with any geometric object, so it is impossible to extend them using a traits-class decorator. Extending the Dcel face records comes handy is such cases. As a matter of fact, it is possible to conveniently extend all Dcel records (namely vertices, halfedges and faces), which can also be advantageous for some applications.
All examples presented so far use the default Arr_default_dcel<Traits>. This is done implicitly, as this class serves as a default parameter for the Arrangement_2 template. The default Dcel class just associates points with vertices and x-monotone curves with halfedge, but nothing more. In this section we show how to use alternative Dcel types to extend the desired Dcel records.
31.8.1 Extending the Dcel Faces
The Arr_face_extended_dcel<Traits, FaceData> class-template is used to associate auxiliary data field of type FaceData to each face record in the Dcel.
When an Arrangement_2 object is parameterized by this Dcel class, its nested Face type is extended with the access function data() and with the modifier set_data(). Using these extra functions it is straightforward to access and maintain the auxiliary face-data field.
Note that the extra data fields must be maintained by the application programmers. They may choose to construct their arrangement, and only then go over the faces and attach the appropriate data fields to the arrangement faces. However, in some cases the face data can only be computed when the face is created (split from another face, or merged with another face). In such cases one can use an arrangement observer tailored for this task, which receives updates whenever a face is modified and sets its data field accordingly.
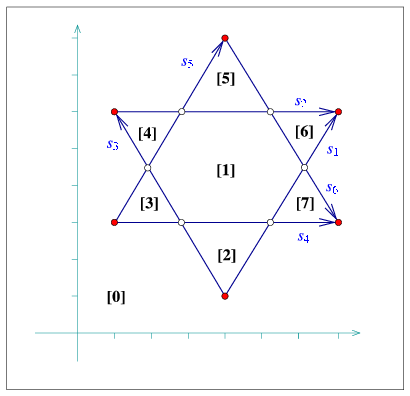
The next example constructs an arrangement that contains seven bounded faces induced by six line segments (see Figure 31.25). An observer gets notified each time a new face f is created and it associates f with a running index, (where the index of the unbounded face is 0). As a result, the faces are numbered according to their creation order, as one can easily verify by examining the insertion order of the segments:20
File: examples/Arrangement_on_surface_2/face_extension.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arr_observer.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2, int> Dcel;
typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2;
// An arrangement observer, used to receive notifications of face splits and
// to update the indices of the newly created faces.
class Face_index_observer : public CGAL::Arr_observer<Arrangement_2>
{
private:
int n_faces; // The current number of faces.
public:
Face_index_observer (Arrangement_2& arr) :
CGAL::Arr_observer<Arrangement_2> (arr),
n_faces (0)
{
CGAL_precondition (arr.is_empty());
arr.unbounded_face()->set_data (0);
n_faces++;
}
virtual void after_split_face (Face_handle /* old_face */,
Face_handle new_face, bool )
{
// Assign index to the new face.
new_face->set_data (n_faces);
n_faces++;
}
};
int main ()
{
// Construct the arrangement containing two intersecting triangles.
Arrangement_2 arr;
Face_index_observer obs (arr);
Segment_2 s1 (Point_2(4, 1), Point_2(7, 6));
Segment_2 s2 (Point_2(1, 6), Point_2(7, 6));
Segment_2 s3 (Point_2(4, 1), Point_2(1, 6));
Segment_2 s4 (Point_2(1, 3), Point_2(7, 3));
Segment_2 s5 (Point_2(1, 3), Point_2(4, 8));
Segment_2 s6 (Point_2(4, 8), Point_2(7, 3));
insert_non_intersecting_curve (arr, s1);
insert_non_intersecting_curve (arr, s2);
insert_non_intersecting_curve (arr, s3);
insert (arr, s4);
insert (arr, s5);
insert (arr, s6);
// Go over all arrangement faces and print the index of each face and it
// outer boundary. The face index is stored in its data field in our case.
Arrangement_2::Face_const_iterator fit;
Arrangement_2::Ccb_halfedge_const_circulator curr;
std::cout << arr.number_of_faces() << " faces:" << std::endl;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit) {
std::cout << "Face no. " << fit->data() << ": ";
if (fit->is_unbounded())
std::cout << "Unbounded." << std::endl;
else {
curr = fit->outer_ccb();
std::cout << curr->source()->point();
do {
std::cout << " --> " << curr->target()->point();
++curr;
} while (curr != fit->outer_ccb());
std::cout << std::endl;
}
}
return 0;
}
31.8.2 Extending All Dcel Records
The Arr_extended_dcel<Traits, VertexData, HalfedgeData, FaceData> class-template is used to associate auxiliary data fields of types VertexData HalfedgeData, and FaceData to each Dcel vertex, halfedge, and face record types, respectively.
When an Arrangement_2 object is injected with this Dcel class, each one of its nested Vertex, Halfedge and Face classes is extended by the access function data() and by the modifier set_data().
The next example shows how to use a Dcel with extended vertex, halfedge, and face records. In this example each vertex is associated with a color, which may be blue, red, or white, depending on whether the vertex is isolated, represents a segment endpoint, or whether it represents an intersection point. Each halfedge is associated with Boolean flag indicating whether its direction is the same as the direction of its associated segment (in this example segments are treated as directed objects). Each face is also extended to store the size of its outer boundary.
The constructed arrangement, depicted in Figure 31.25, is similar to the arrangement constructed in the previous example. Note that all auxiliary data fields are set during the construction phase. Also note that the data fields are properly maintained when the arrangement is copied to another arrangement instance:
File: examples/Arrangement_on_surface_2/dcel_extension.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_extended_dcel.h>
enum Color {BLUE, RED, WHITE};
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arr_extended_dcel<Traits_2,Color, bool, int> Dcel;
typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2;
int main ()
{
// Construct the arrangement containing two intersecting triangles.
Arrangement_2 arr;
Segment_2 s1 (Point_2(4, 1), Point_2(7, 6));
Segment_2 s2 (Point_2(1, 6), Point_2(7, 6));
Segment_2 s3 (Point_2(4, 1), Point_2(1, 6));
Segment_2 s4 (Point_2(1, 3), Point_2(7, 3));
Segment_2 s5 (Point_2(1, 3), Point_2(4, 8));
Segment_2 s6 (Point_2(4, 8), Point_2(7, 3));
insert_non_intersecting_curve (arr, s1);
insert_non_intersecting_curve (arr, s2);
insert_non_intersecting_curve (arr, s3);
insert (arr, s4);
insert (arr, s5);
insert (arr, s6);
// Go over all arrangement vertices and set their colors according to our
// coloring convention.
Arrangement_2::Vertex_iterator vit;
unsigned int degree;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit)
{
degree = vit->degree();
if (degree == 0)
vit->set_data (BLUE); // Isolated vertex.
else if (degree <= 2)
vit->set_data (RED); // Vertex represents an endpoint.
else
vit->set_data (WHITE); // Vertex represents an intersection point.
}
// Go over all arrangement edges and set their flags.
Arrangement_2::Edge_iterator eit;
bool flag;
for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit) {
// Check if the halfegde has the same diretion as its associated
// segment. Note that its twin always has an opposite direction.
flag = (eit->source()->point() == eit->curve().source());
eit->set_data (flag);
eit->twin()->set_data (!flag);
}
// For each arrangement face, print the outer boundary and its size.
Arrangement_2::Face_iterator fit;
Arrangement_2::Ccb_halfedge_circulator curr;
int boundary_size;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit) {
boundary_size = 0;
if (! fit->is_unbounded()) {
curr = fit->outer_ccb();
do {
++boundary_size;
++curr;
} while (curr != fit->outer_ccb());
}
fit->set_data (boundary_size);
}
// Copy the arrangement and print the vertices.
Arrangement_2 arr2 = arr;
std::cout << "The arrangement vertices:" << std::endl;
for (vit = arr2.vertices_begin(); vit != arr2.vertices_end(); ++vit) {
std::cout << '(' << vit->point() << ") - ";
switch (vit->data()) {
case BLUE : std::cout << "BLUE." << std::endl; break;
case RED : std::cout << "RED." << std::endl; break;
case WHITE : std::cout << "WHITE." << std::endl; break;
}
}
return 0;
}
31.9 Overlaying Arrangements
Assume that we are given two geographic maps represented as arrangements with some data objects attached to their faces, representing some geographic information - for example, a map of the annual precipitation in some country and a map of the vegetation in the same country. It is interesting to overlay the two maps to locate, for example, the regions where there is a pine forest and the annual precipitation is between 1000 mm and 1500 mm.
Computing the overlay of two planar arrangement is also useful for supporting Boolean set operations on polygons (or generalized polygons, see, e.g., [BEH+02]).
The function overlay (arr_a, arr_b, ovl_arr, ovl_traits) accepts two input arrangement instances arr_a and arr_b, and constructs their overlay instance ovl_arr. All three arrangements must use the same geometric primitives. More precisely, let arr_a be of type Arrangement_2<Traits_A,Dcel_A>, arr_b be of type Arrangement_2<Traits_B,Dcel_B> and the resulting ovl_arr be of type Arrangement_2<Traits_R,Dcel_R>. All types nested in geometry traits Traits_A, e.g., Point_2 and X_monotone_curve_2, must be convertible to the corresponding types nested in geometry traits Traits_R. The same holds for all types nested in geometry traits Traits_B. The ovl_traits parameter is an instance of an overlay traits-class, which enables the creation of Dcel_R records in the overlaid arrangement from the Dcel features of arr_a and arr_b that they correspond to.
In principle, we distinguish between three levels of overlay:
- Simple overlay:
-
An overlay of two arrangements that store no additional data
with their Dcel records. That is, they are defined using the default
Dcel class Arr_default_dcel. Typically, the overlaid
arrangement in this case stores no extra data with its Dcel records as
well (or if it does, the additional data fields cannot be computed by
the overlay operation), so by overlaying the two arrangement we just
compute the arrangement of all curves that induce arr_a and arr_b.
Note that the same result can be obtained using the standard insertion
operations, but users may choose to use overlay computation in order to
achieve better running times.
The Arr_default_overlay_traits class should be used as an overlay traits-class for such simple overlay operations.
- Face overlay:
-
An overlay of two arrangements that store additional data
fields with their faces (e.g., the geographic-map example
given in the beginning of this section). The resulting overlaid arrangement
typically also stores extraneous data fields with its faces, where the
data field that is attached to an overlaid face can be computed from the
data fields of the two faces (in arr_a and arr_b) that induce
the overlaid face.
The Arr_face_overlay_traits class should be used as an overlay traits-class for face-overlay operations. It operates on arrangement, whose Dcel representation is based on the Arr_face_extended_dcel class-template (see Section 31.8.1). The face-overlay traits-class is parameterized by a functor that is capable of combining two face-data fields of types Dcel_A::Face_data and Dcel_B::Face_data, and computing the output Dcel_R::Face_data object. The overlay traits-class uses this functor to properly construct the overlaid faces.
- Full overlay:
- An overlay of two arrangements that store additional data fields with all their Dcel records. That is, their Dcel classes are instantiations of the Arr_extended_dcel class-template (see Section 31.8.2), where the resulting arrangement also extends it Dcel records with data fields computed on the basis of the overlapping Dcel features of the two input arrangements.
In the following subsections we give some examples for the simple and the face-overlay operations and demonstrate how to use the auxiliary overlay traits-classes. For the full overlay operations users need to implement their specialized overlay traits-class, which models the OverlayTraits concept. The details of this concept are given in the Reference Manual.
31.9.1 Example for a Simple Overlay
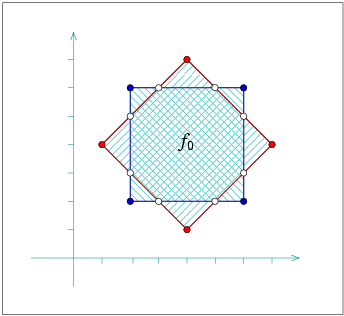
The next program constructs two simple arrangements, as depicted in Figure 31.26 and computes their overlay:
File: examples/Arrangement_on_surface_2/overlay.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_overlay_2.h>
#include <CGAL/Arr_default_overlay_traits.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
typedef CGAL::Arr_default_overlay_traits<Arrangement_2> Overlay_traits;
int main ()
{
// Construct the first arrangement, containing a square-shaped face.
Arrangement_2 arr1;
Segment_2 s1 (Point_2(2, 2), Point_2(6, 2));
Segment_2 s2 (Point_2(6, 2), Point_2(6, 6));
Segment_2 s3 (Point_2(6, 6), Point_2(2, 6));
Segment_2 s4 (Point_2(2, 6), Point_2(2, 2));
insert_non_intersecting_curve (arr1, s1);
insert_non_intersecting_curve (arr1, s2);
insert_non_intersecting_curve (arr1, s3);
insert_non_intersecting_curve (arr1, s4);
// Construct the second arrangement, containing a rhombus-shaped face.
Arrangement_2 arr2;
Segment_2 t1 (Point_2(4, 1), Point_2(7, 4));
Segment_2 t2 (Point_2(7, 4), Point_2(4, 7));
Segment_2 t3 (Point_2(4, 7), Point_2(1, 4));
Segment_2 t4 (Point_2(1, 4), Point_2(4, 1));
insert_non_intersecting_curve (arr2, t1);
insert_non_intersecting_curve (arr2, t2);
insert_non_intersecting_curve (arr2, t3);
insert_non_intersecting_curve (arr2, t4);
// Compute the overlay of the two arrangements.
Arrangement_2 overlay_arr;
Overlay_traits overlay_traits;
overlay (arr1, arr2, overlay_arr, overlay_traits);
// Print the size of the overlaid arrangement.
std::cout << "The overlaid arrangement size:" << std::endl
<< " V = " << overlay_arr.number_of_vertices()
<< ", E = " << overlay_arr.number_of_edges()
<< ", F = " << overlay_arr.number_of_faces() << std::endl;
return 0;
}
31.9.2 Examples for a Face Overlay
The following example shows how to compute the intersection of two polygons using the overlay() function. It uses a face-extended Dcel class to define our arrangement class. The Dcel extends each face with a Boolean flag. A polygon is represented as a marked arrangement face, (whose flag is set). The example uses a face-overlay traits class, instantiated with a functor that simply performs a logical and operations on Boolean flags. As a result, a face in the overlaid arrangement is marked only when it corresponds to an overlapping region of two marked cells in the input arrangements. Namely, it is part of the intersection of the two polygons.
The example computes the intersection between a square and a rhombus, (which is actually also a square). The resulting polygon is an octagon, denoted by f0 in Figure 31.26:
File: examples/Arrangement_on_surface_2/face_extension_overlay.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arr_overlay_2.h>
#include <CGAL/Arr_default_overlay_traits.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2, bool> Dcel;
typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2;
typedef CGAL::Arr_face_overlay_traits<Arrangement_2,
Arrangement_2,
Arrangement_2,
std::logical_and<bool> > Overlay_traits;
int main ()
{
// Construct the first arrangement, containing a square-shaped face.
Arrangement_2 arr1;
Segment_2 s1 (Point_2(2, 2), Point_2(6, 2));
Segment_2 s2 (Point_2(6, 2), Point_2(6, 6));
Segment_2 s3 (Point_2(6, 6), Point_2(2, 6));
Segment_2 s4 (Point_2(2, 6), Point_2(2, 2));
insert_non_intersecting_curve (arr1, s1);
insert_non_intersecting_curve (arr1, s2);
insert_non_intersecting_curve (arr1, s3);
insert_non_intersecting_curve (arr1, s4);
// Mark just the bounded face.
Arrangement_2::Face_iterator fit;
CGAL_assertion (arr1.number_of_faces() == 2);
for (fit = arr1.faces_begin(); fit != arr1.faces_end(); ++fit)
fit->set_data (fit != arr1.unbounded_face());
// Construct the second arrangement, containing a rhombus-shaped face.
Arrangement_2 arr2;
Segment_2 t1 (Point_2(4, 1), Point_2(7, 4));
Segment_2 t2 (Point_2(7, 4), Point_2(4, 7));
Segment_2 t3 (Point_2(4, 7), Point_2(1, 4));
Segment_2 t4 (Point_2(1, 4), Point_2(4, 1));
insert_non_intersecting_curve (arr2, t1);
insert_non_intersecting_curve (arr2, t2);
insert_non_intersecting_curve (arr2, t3);
insert_non_intersecting_curve (arr2, t4);
// Mark just the bounded face.
CGAL_assertion (arr2.number_of_faces() == 2);
for (fit = arr2.faces_begin(); fit != arr2.faces_end(); ++fit)
fit->set_data (fit != arr2.unbounded_face());
// Compute the overlay of the two arrangements, marking only the faces that
// are intersections of two marked faces in arr1 and arr2, respectively.
Arrangement_2 overlay_arr;
Overlay_traits overlay_traits;
overlay (arr1, arr2, overlay_arr, overlay_traits);
// Go over the faces of the overlaid arrangement and print just the marked
// ones.
Arrangement_2::Ccb_halfedge_circulator curr;
std::cout << "The union is: ";
for (fit = overlay_arr.faces_begin(); fit != overlay_arr.faces_end(); ++fit) {
if (! fit->data())
continue;
curr = fit->outer_ccb();
std::cout << curr->source()->point();
do {
std::cout << " --> " << curr->target()->point();
++curr;
} while (curr != fit->outer_ccb());
std::cout << std::endl;
}
return 0;
}
The next example demonstrates the face overlay of two arrangements that have unbounded faces as well. The first arrangement is formed by the two lines y = x and y = -x, that subdivide the plane into four unbounded faces, denoted A, B, C and D. The second arrangement comprises four line segments that form a square-shaped face. When we overlay the two arrangements, each of the four faces A, B, C and D is split into an unbounded face (indexed 1) and a bounded face (indexed 2):
File: examples/Arrangement_on_surface_2/overlay_unbounded.cpp
#include <string>
#include <boost/lexical_cast.hpp>
#include <CGAL/Exact_predicates_exact_constructions_kernel.h>
#include <CGAL/Arr_linear_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arr_overlay_2.h>
#include <CGAL/Arr_default_overlay_traits.h>
// Define a functor for creating a label from a characer and an integer.
struct Overlay_label
{
std::string operator() (char c, int i) const
{
return boost::lexical_cast<std::string>(c) +
boost::lexical_cast<std::string>(i);
}
};
typedef CGAL::Exact_predicates_exact_constructions_kernel Kernel;
typedef CGAL::Arr_linear_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Segment_2 Segment_2;
typedef Traits_2::Ray_2 Ray_2;
typedef Traits_2::Line_2 Line_2;
typedef Traits_2::X_monotone_curve_2 X_monotone_curves_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2, char> DcelA;
typedef CGAL::Arrangement_2<Traits_2, DcelA> ArrangementA_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2, int> DcelB;
typedef CGAL::Arrangement_2<Traits_2, DcelB> ArrangementB_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2, std::string> DcelRes;
typedef CGAL::Arrangement_2<Traits_2, DcelRes> ArrangementRes_2;
typedef CGAL::Arr_face_overlay_traits<ArrangementA_2,
ArrangementB_2,
ArrangementRes_2,
Overlay_label> Overlay_traits;
int main ()
{
// Construct the first arrangement, induced by two line y = x and y = -x.
ArrangementA_2 arr1;
insert (arr1, Line_2 (Point_2(0, 0), Point_2(1, 1)));
insert (arr1, Line_2 (Point_2(0, 0), Point_2(1, -1)));
// Label the four (unbounded) face of the arrangement as 'A' to 'D'.
// We do so by traversing the incident faces to the halfedges aroung the
// single arrangement vertex (0, 0).
CGAL_assertion (arr1.number_of_vertices() == 1);
ArrangementA_2::Halfedge_around_vertex_circulator first, curr;
char clabel = 'A';
curr = first = arr1.vertices_begin()->incident_halfedges();
do {
curr->face()->set_data (clabel);
++clabel;
++curr;
} while (curr != first);
std::cout << "Done with arr1." << std::endl;
// Construct the second arrangement, containing a single square-shaped face.
ArrangementB_2 arr2;
insert (arr2, Segment_2 (Point_2(-4, -4), Point_2(4, -4)));
insert (arr2, Segment_2 (Point_2(4, -4), Point_2(4, 4)));
insert (arr2, Segment_2 (Point_2(4, 4), Point_2(-4, 4)));
insert (arr2, Segment_2 (Point_2(-4, 4), Point_2(-4, -4)));
// Give the unbounded face the index 1, and the bounded face the index 2.
CGAL_assertion (arr2.number_of_faces() == 2);
ArrangementB_2::Face_iterator fit;
for (fit = arr2.faces_begin(); fit != arr2.faces_end(); ++fit)
fit->set_data ((fit == arr2.unbounded_face()) ? 1 : 2);
std::cout << "Done with arr2." << std::endl;
// Compute the overlay of the two arrangements.
ArrangementRes_2 overlay_arr;
Overlay_traits overlay_traits;
overlay (arr1, arr2, overlay_arr, overlay_traits);
// Go over the faces of the overlaid arrangement and their labels.
ArrangementRes_2::Face_iterator res_fit;
std::cout << "The overlay faces are: ";
for (res_fit = overlay_arr.faces_begin();
res_fit != overlay_arr.faces_end(); ++res_fit)
{
std::cout << res_fit->data() << " ("
<< (res_fit->is_unbounded() ? "unbounded" : "bounded")
<< ")." << std::endl;
}
return 0;
}
31.10 Storing the Curve History
As stated at the beginning of this chapter (Section 31.1), when one constructs an arrangement induced by a set C of arbitrary planar curves, she or he constructs a collection C'' of x-monotone subcurves of C that are pairwise disjoint in their interior, and these subcurves are associated with the arrangement edges (more precisely, with the Dcel halfedges). Doing so, the connection between the originating input curves and the arrangement edges is lost. This loss might be acceptable for some applications. However, in many practical cases it is important to determine the input curves that give rise to the final subcurves.
The Arrangement_with_history_2<Traits,Dcel> class-template extends the Arrangement_2 class by keeping an additional container of input curves representing C, and by maintaining a cross-mapping between these curves and the arrangement edges they induce. The traits class that is used for instantiating the template should be a model of the ArrangementTraits_2 concept (see Section 31.4.1.3). That is, it should define the Curve_2 type (and not just the X_monotone_curve_2 type). The Dcel parameter should model the ArrangementDcel concept. Users can use the default Dcel class or an extended Dcel class according to their needs.
31.10.1 Traversing an Arrangement with History
The Arrangement_with_history_2 class extends the Arrangement_2 class, thus all the iterator and circulator types that are defined by the arrangement class are also available in Arrangement_with_history_2. The reader is referred to Section 31.2.2 for a comprehensive review of these functions.
As mentioned above, the Arrangement_with_history_2 class maintains a container of input curves, which can be accessed using curve handles. The member function number_of_curves() returns the number of input curves stored in the container, while curves_begin() and curves_end() return Arrangement_with_history_2::Curve_iterator objects that define the valid range of curves that induce the arrangement. The value type of this iterator is Curve_2. Moreover, the curve-iterator type is equivalent to Arrangement_with_history_2::Curve_handle, which is used for accessing the stored curves. Conveniently, the corresponding constant-iterator and constant-handle types are also defined.
As mentioned in the previous paragraph, a Curve_handle object ch serves as a pointer to a curve stored in an arrangement-with-history instance arr. Using this handle, it is possible to obtain the number of arrangement edges this curve induces by calling arr.number_of_induced_edges(ch). The functions arr.induced_edges_begin(ch) and arr.induced_edges_end(ch) return iterators of type Arrangement_with_history_2::Induced_edges_iterator that define the valid range of edges induced by ch. The value type of these iterators is Halfedge_handle. It is thus possible to traverse all arrangement edges induced by an input curve.
It is also important to be able to perform the inverse mapping. Given an arrangement edge, we would like to be able to determine which input curve induces it. In case the edge represents an overlap of several curves, we should be able to trace all input curves that overlap over this edge. The Arrangement_with_history_2 class is extended by several member functions that enable such an inverse mapping. Given a halfedge handle e in an arrangement with history arr, then arr.number_of_originating_curves(e) returns the number of curves that induce the edge (which should be 1 in non-degenerate cases, and 2 or more in case of overlaps), while arr.originating_curves_begin(e) and arr.originating_curves_end(e) return Arrangement_with_history_2::Originating_curve_iterator objects that define the range of curves that induce e. The value type of these iterator is Curve_2.
It is possible to overlay two Arrangement_with_history_2 instances instantiated by the same traits class. In this case, the resulting arrangement will store a consolidated container of input curves, and automatically preserve the cross-mapping between the arrangement edges and the consolidated curve set. Users can employ an overlay-traits class to maintain any type of auxiliary data stored with the Dcel features (see Section 31.9).
31.10.2 Modifying an Arrangement with History
As the Arrangement_with_history_2 class extends the Arrangement_2 class, it inherits the fundamental modification operations, such as assign() and clear(), from it. The vertex-manipulation functions are also inherited and supported (see Sections 31.2.3.2 and 31.4.1.4 for the details). However, there are some fundamental differences between the interfaces of the two classes, which we highlight in this subsection.
The most significant difference between the arrangement-with-history class and the basic arrangement class is the way they handle their input curves. Arrangement_with_history_2 always stores the Curve_2 objects that induce it, thus it is impossible to insert x-monotone curves into an arrangement with history. The free insert_non_intersecting_curve() and insert() that receives x-monotone curve (as well as their aggregated versions) are therefore not available for arrangement-with-history instances and only the free insert() and insert() functions that receive Curve_2 (the incremental insertion function and the aggregated insertion function) are supported - see also Section 31.4.1.3. Notice however that while the incremental insertion function insert(arr,c) for an Arrangement_2 object arr does not have a return value, the corresponding arrangement-with-history function returns a Curve_handle to the inserted curve.
As we are able to keep track of all edges induced by an input curve, we also provide a free function that removes a curve from an arrangement. By calling remove(arr,ch), where ch is a valid curve handle, the given curve is deleted from the curve container, and all edges induced solely by this curve (i.e., excluding overlapping edges) are removed from the arrangement. The function returns the number of edges that have been removed.
In some cases, users may need to operate directly on the arrangement edges. We first mention that the specialized insertion functions (see Section 31.2.3.1) are not supported, as they accept x-monotone curves. Insertion can only be performed via the free insertion-functions. The other edge-manipulation functions (see Section 31.2.3.3) are however available, but have a different interface that does not use x-monotone curves:
- Invoking split_edge(e,p) splits the edge e at a given point p that lies in its interior.
- Invoking merge_edge(e1,e2) merges the two given edges. There is a precondition that e1 and e2 shared a common end-vertex of degree 2, and that the x-monotone subcurves associated with these edges are mergeable.
- It is possible to remove an edge by simply invoking remove_edge(e).
It should be noted that it is possible to attach observers to an arrangement-with-history instance in order to get detailed notifications of the changes the arrangements undergoes (see Section 31.7 for the details).
31.10.3 Examples
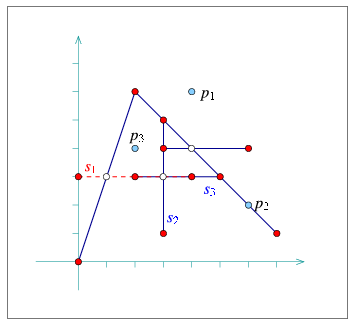
In the following example we construct a simple arrangement of six line segments, as depicted in Figure 31.27, while maintaining the curve history. The example demonstrates the usage of the special traversal functions. It also shows how to issue point-location queries on the resulting arrangement, using the auxiliary function point_location_query() defined in the header file point_location_utils.h (see also Section 31.3.1).
File: examples/Arrangement_on_surface_2/curve_history.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_on_surface_with_history_2.h>
#include <CGAL/Arrangement_with_history_2.h>
#include <CGAL/Arr_simple_point_location.h>
#include "point_location_utils.h"
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Segment_2;
typedef CGAL::Arrangement_with_history_2<Traits_2> Arr_with_hist_2;
typedef Arr_with_hist_2::Curve_handle Curve_handle;
typedef CGAL::Arr_simple_point_location<Arr_with_hist_2> Point_location;
int main ()
{
Arr_with_hist_2 arr;
// Insert s1, s2 and s3 incrementally:
Segment_2 s1 (Point_2 (0, 3), Point_2 (4, 3));
Curve_handle c1 = insert (arr, s1);
Segment_2 s2 (Point_2 (3, 2), Point_2 (3, 5));
Curve_handle c2 = insert (arr, s2);
Segment_2 s3 (Point_2 (2, 3), Point_2 (5, 3));
Curve_handle c3 = insert (arr, s3);
// Insert three additional segments aggregately:
Segment_2 segs[3];
segs[0] = Segment_2 (Point_2 (2, 6), Point_2 (7, 1));
segs[1] = Segment_2 (Point_2 (0, 0), Point_2 (2, 6));
segs[2] = Segment_2 (Point_2 (3, 4), Point_2 (6, 4));
insert (arr, segs, segs + 3);
// Print out the curves and the number of edges each one induces.
Arr_with_hist_2::Curve_iterator cit;
std::cout << "The arrangement contains "
<< arr.number_of_curves() << " curves:" << std::endl;
for (cit = arr.curves_begin(); cit != arr.curves_end(); ++cit)
std::cout << "Curve [" << *cit << "] induces "
<< arr.number_of_induced_edges(cit) << " edges." << std::endl;
// Print the arrangement edges, along with the list of curves that
// induce each edge.
Arr_with_hist_2::Edge_iterator eit;
Arr_with_hist_2::Originating_curve_iterator ocit;
std::cout << "The arrangement is comprised of "
<< arr.number_of_edges() << " edges:" << std::endl;
for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit) {
std::cout << "[" << eit->curve() << "]. Originating curves: ";
for (ocit = arr.originating_curves_begin (eit);
ocit != arr.originating_curves_end (eit); ++ocit)
{
std::cout << " [" << *ocit << "]" << std::flush;
}
std::cout << std::endl;
}
// Perform some point-location queries:
Point_location pl (arr);
Point_2 p1 (4, 6);
point_location_query (pl, p1);
Point_2 p2 (6, 2);
point_location_query (pl, p2);
Point_2 p3 (2, 4);
point_location_query (pl, p3);
return 0;
}
The following example demonstrates the usage of the free remove() function. We construct an arrangement of nine circles, while keeping a handle to each inserted circle. We then remove the large circle C0, which induces 18 edges, as depicted in Figure 31.28. The example also shows how to use the split_edge() and merge_edge() functions when operating on an arrangement-with-history instance:
File: examples/Arrangement_on_surface_2/edge_manipulation_curve_history.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_circle_segment_traits_2.h>
#include <CGAL/Arrangement_with_history_2.h>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef Kernel::Point_2 Rat_point_2;
typedef Kernel::Circle_2 Circle_2;
typedef CGAL::Arr_circle_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Curve_2;
typedef CGAL::Arrangement_with_history_2<Traits_2> Arr_with_hist_2;
typedef Arr_with_hist_2::Curve_handle Curve_handle;
typedef CGAL::Arr_walk_along_line_point_location<Arr_with_hist_2>
Point_location;
int main ()
{
// Construct an arrangement containing nine circles: C[0] of radius 2 and
// C[1], ..., C[8] of radius 1.
const Number_type _7_halves = Number_type (7, 2);
Arr_with_hist_2 arr;
Curve_2 C[9];
Curve_handle handles[9];
int k;
C[0] = Circle_2 (Rat_point_2 (_7_halves, _7_halves), 4, CGAL::CLOCKWISE);
C[1] = Circle_2 (Rat_point_2 (_7_halves, 6), 1, CGAL::CLOCKWISE);
C[2] = Circle_2 (Rat_point_2 (5, 6), 1, CGAL::CLOCKWISE);
C[3] = Circle_2 (Rat_point_2 (6, _7_halves), 1, CGAL::CLOCKWISE);
C[4] = Circle_2 (Rat_point_2 (5, 2), 1, CGAL::CLOCKWISE);
C[5] = Circle_2 (Rat_point_2 (_7_halves, 1), 1, CGAL::CLOCKWISE);
C[6] = Circle_2 (Rat_point_2 (2, 2), 1, CGAL::CLOCKWISE);
C[7] = Circle_2 (Rat_point_2 (1, _7_halves), 1, CGAL::CLOCKWISE);
C[8] = Circle_2 (Rat_point_2 (2, 5), 1, CGAL::CLOCKWISE);
for (k = 0; k < 9; k++)
handles[k] = insert (arr, C[k]);
std::cout << "The initial arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Remove the large circle C[0].
std::cout << "Removing C[0] : ";
std::cout << remove_curve (arr, handles[0])
<< " edges have been removed." << std::endl;
std::cout << "The arrangement size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Locate the point q, which should be on an edge e.
Point_location pl (arr);
const Point_2 q = Point_2 (_7_halves, 7);
CGAL::Object obj = pl.locate (q);
Arr_with_hist_2::Halfedge_const_handle e;
CGAL_assertion_code(bool success = ) CGAL::assign (e, obj);
CGAL_assertion (success);
// Split the edge e to two edges e1 and e2;
Arr_with_hist_2::Halfedge_handle e1, e2;
e1 = arr.split_edge (arr.non_const_handle (e), q);
e2 = e1->next();
std::cout << "After edge split: "
<< "V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Merge back the two split edges.
arr.merge_edge (e1, e2);
std::cout << "After edge merge: "
<< "V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
return 0;
}
31.11 Input/Output Streams
In some cases, one would like to save an arrangement object constructed by some application, so that later on it can be restored. In other cases one would like to create nice drawings that represent arrangements constructed by some application. These drawings can be hard printed or displayed on a computer screen.
31.11.1 Input/Output Stream
Consider an arrangement that represents a very complicated geographical map, and assume that there are various applications that need to answer point-location queries on this map. Naturally, you can store the set of curves that induces the arrangement, but this implies that you would need to construct the arrangement from scratch each time you need to reuse it. A more efficient solution is to write the arrangement to a file in a format that other applications can read.This package provides an inserter (the << operator) and an extractor (the >> operator) for the Arrangement_2<Traits,Dcel> class that inserts and an arrangement object into an output stream and extracts an arrangement object from an input stream respectively. The arrangement is written using a simple predefined ASCII format that encodes the arrangement topology, as well as all geometric entities associated with vertices and edges.
The ability to use the input/output operators, requires that the Point_2 type and the X_monotone_curve_2 type defined by the traits class both support the << and >> operators. The Arr_conic_traits_2 class (see Section 31.6.5), the Arr_rational_function_traits_2 class (see Section 31.6.6), and the Arr_linear_traits_2 class (see Section 31.6.2) currently do not provide these operators for the geometric types they define. Thus, only arrangements of line segments or of polylines can be written or read.
The following example constructs the arrangement depicted in Figure 31.7 and writes it to an output file. It also demonstrates how to re-read the arrangement from a file:
File: examples/Arrangement_on_surface_2/io.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/IO/Arr_iostream.h>
#include <fstream>
#include "point_location_utils.h"
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
int main ()
{
// Construct the arrangement.
Arrangement_2 arr;
construct_segments_arr (arr);
std::cout << "Writing an arrangement of size:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Write the arrangement to a file.
std::ofstream out_file ("arr_ex_io.dat");
out_file << arr;
out_file.close();
// Read the arrangement from the file.
Arrangement_2 arr2;
std::ifstream in_file ("arr_ex_io.dat");
in_file >> arr2;
in_file.close();
std::cout << "Read an arrangement of size:" << std::endl
<< " V = " << arr2.number_of_vertices()
<< ", E = " << arr2.number_of_edges()
<< ", F = " << arr2.number_of_faces() << std::endl;
return (0);
}
31.11.2 Arrangements with Auxiliary Data
The inserter and extractor both ignore any auxiliary data stored with the arrangement features. Thus, they are ideal for arrangements instantiated using the Arr_default_dcel class. However, as explained in Section 31.8, one can easily extend the arrangement faces by using the Arr_face_extended_dcel template, or extend all Dcel records by using the Arr_extended_dcel template. In such cases, it might be crucial that the auxiliary data fields are written to the file and read from there.
The arrangement package includes the free functions write(arr, os, formatter), which writes the arrangement arr to an output stream os, and read(arr, os, formatter), which reads the arrangement arr from an input stream is. Both operations are performed using a formatter object, which defines the I/O format. The package contains three formatter classes:
- Arr_text_formatter<Arrangement> defines a simple textual I/O format for the arrangement topology and geometry, disregarding any auxiliary data that may be associated with the arrangement features. This is the default formatter used by the arrangement inserter and the arrangement extractor, as defined above.
- Arr_face_extended_text_formatter<Arrangement> operates on arrangements whose Dcel representation is based on the Arr_face_extended_dcel<Traits,FaceData> class (see Section 31.8.1). It supports reading and writing the auxiliary data objects stored with the arrangement faces provided that the FaceData class supports an inserter and an extractor.
- Arr_extended_dcel_text_formatter<Arrangement> operates on arrangements whose Dcel representation is based on the Arr_extended_dcel<Traits,VertexData,HalfedgeData,FaceData> class (see Section 31.8.2). It supports reading and writing the auxiliary data objects stored with the arrangement vertices, edges and faces, provided that the VertexData, HalfedgeData and FaceData classed all have inserters and extractors.
The following example constructs the same arrangement as the example dcel_extension does (see Section 31.8.2), depicted in Figure 31.25, and writes it to an output file. It also demonstrates how to re-read the arrangement from a file:
File: examples/Arrangement_on_surface_2/dcel_extension_io.cpp
#include "arr_rational_nt.h" #include <CGAL/Cartesian.h> #include <CGAL/Arr_segment_traits_2.h> #include <CGAL/Arr_extended_dcel.h> #include <CGAL/Arrangement_2.h> #include <CGAL/IO/Arr_text_formatter.h> #include <CGAL/IO/Arr_iostream.h> #include <fstream> enum Color {BLUE, RED, WHITE}; std::ostream& operator<< (std::ostream& os, const Color& color) { switch (color) { case BLUE: os << "BLUE"; break; case RED: os << "RED"; break; case WHITE: os << "WHITE"; break; default: os << "ERROR!"; } return (os); } std::istream& operator>> (std::istream& is, Color& color) { std::string str; is >> str; if (str == "BLUE") color = BLUE; else if (str == "RED") color = RED; else if (str == "WHITE") color = WHITE; return (is); } typedef CGAL::Cartesian<Number_type> Kernel; typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2; typedef Traits_2::Point_2 Point_2; typedef Traits_2::X_monotone_curve_2 Segment_2; typedef CGAL::Arr_extended_dcel<Traits_2, Color, bool, int> Dcel; typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2; typedef CGAL::Arr_extended_dcel_text_formatter<Arrangement_2> Formatter; int main () { // Construct the arrangement containing two intersecting triangles. Arrangement_2 arr; Segment_2 s1 (Point_2(4, 1), Point_2(7, 6)); Segment_2 s2 (Point_2(1, 6), Point_2(7, 6)); Segment_2 s3 (Point_2(4, 1), Point_2(1, 6)); Segment_2 s4 (Point_2(1, 3), Point_2(7, 3)); Segment_2 s5 (Point_2(1, 3), Point_2(4, 8)); Segment_2 s6 (Point_2(4, 8), Point_2(7, 3)); insert_non_intersecting_curve (arr, s1); insert_non_intersecting_curve (arr, s2); insert_non_intersecting_curve (arr, s3); insert (arr, s4); insert (arr, s5); insert (arr, s6); // Go over all arrangement vertices and set their colors. Arrangement_2::Vertex_iterator vit; unsigned int degree; for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit) { degree = vit->degree(); if (degree == 0) vit->set_data (BLUE); // Isolated vertex. else if (degree <= 2) vit->set_data (RED); // Vertex represents an endpoint. else vit->set_data (WHITE); // Vertex represents an intersection point. } // Go over all arrangement edges and set their flags. Arrangement_2::Edge_iterator eit; bool flag; for (eit = arr.edges_begin(); eit != arr.edges_end(); ++eit) { // Check if the halfegde has the same diretion as its associated // segment. Note that its twin always has an opposite direction. flag = (eit->source()->point() == eit->curve().source()); eit->set_data (flag); eit->twin()->set_data (!flag); } // Go over all arrangement faces and print their outer boundary and indices. Arrangement_2::Face_iterator fit; Arrangement_2::Ccb_halfedge_circulator curr; int boundary_size; for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit) { boundary_size = 0; if (! fit->is_unbounded()) { curr = fit->outer_ccb(); do { ++boundary_size; ++curr; } while (curr != fit->outer_ccb()); } fit->set_data (boundary_size); } // Write the arrangement to a file. std::ofstream out_file ("arr_ex_dcel_io.dat"); Formatter formatter; write (arr, out_file, formatter); out_file.close(); // Read the arrangement from the file. Arrangement_2 arr2; std::ifstream in_file ("arr_ex_dcel_io.dat"); read (arr2, in_file, formatter); in_file.close(); std::cout << "The arrangement vertices: " << std::endl; for (vit = arr2.vertices_begin(); vit != arr2.vertices_end(); ++vit) std::cout << '(' << vit->point() << ") - " << vit->data() << std::endl; return (0); }
You may develop your own own formatter classes - models of the ArrangementInputFormatter and ArrangementOutputFormatter concepts, as defined in the Reference Manual. Doing so, you can define other I/O formats, such as an XML-based format or a binary format.
31.11.3 Arrangements with Curve History
Section 31.10 introduces the Arrangement_with_history_2<Traits,Dcel> class, which saves the set of curves inducing an arrangement and maintains the relations between these curves and the edges they induce. Naturally, when reading or writing an arrangement-with-history instance we would like this information to be saved to the output stream or restored from the input stream alongside with the basic arrangement structure.
The arrangement package supplies an inserter and an extractor for the Arrangement_with_history_2<Traits,Dcel> class. The arrangement is represented using a simple predefined ASCII format. An object of the Arrangement_with_history_2<Traits,Dcel> type can be saved and restored, as long as the Curve_2 type defined by the traits class - as well as the Point_2 type and the X_monotone_curve_2 types - support the << and>> operators.
The following example constructs the same arrangement as example curve_history does (see Section 31.10.3), depicted in Figure 31.27, and writes it to an output file. It also demonstrates how to re-read the arrangement-with-history from a file:
File: examples/Arrangement_on_surface_2/io_curve_history.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_with_history_2.h>
#include <CGAL/IO/Arr_with_history_iostream.h>
#include <fstream>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::Curve_2 Segment_2;
typedef CGAL::Arrangement_with_history_2<Traits_2> Arr_with_hist_2;
int main ()
{
Arr_with_hist_2 arr;
// Insert six additional segments aggregately:
Segment_2 segs[6];
segs[0] = Segment_2 (Point_2 (2, 6), Point_2 (7, 1));
segs[1] = Segment_2 (Point_2 (3, 2), Point_2 (3, 5));
segs[2] = Segment_2 (Point_2 (2, 3), Point_2 (5, 3));
segs[3] = Segment_2 (Point_2 (2, 6), Point_2 (7, 1));
segs[4] = Segment_2 (Point_2 (0, 0), Point_2 (2, 6));
segs[5] = Segment_2 (Point_2 (3, 4), Point_2 (6, 4));
insert (arr, segs, segs + 6);
std::cout << "Writing an arrangement of "
<< arr.number_of_curves() << " input segments:" << std::endl
<< " V = " << arr.number_of_vertices()
<< ", E = " << arr.number_of_edges()
<< ", F = " << arr.number_of_faces() << std::endl;
// Write the arrangement to a file.
std::ofstream out_file ("arr_ex_io_hist.dat");
out_file << arr;
out_file.close();
// Read the arrangement from the file.
Arr_with_hist_2 arr2;
std::ifstream in_file ("arr_ex_io_hist.dat");
in_file >> arr2;
in_file.close();
std::cout << "Read an arrangement of "
<< arr2.number_of_curves() << " input segments:" << std::endl
<< " V = " << arr2.number_of_vertices()
<< ", E = " << arr2.number_of_edges()
<< ", F = " << arr2.number_of_faces() << std::endl;
return (0);
}
31.11.4 Output Qt-widget Stream
You can display the drawings of arrangements in a graphical window powered by Qt interactively. All you need to do is follow the guidelines for handling Qt_widget objects, and apply the inserter, which inserts an arrangement into a Qt_widget stream to complete the drawing.The ability to use this output operator, requires that the Point_2 and X_monotone_curve_2 types defined by the traits class both support the << operator that inserts the respective geometric object into a Qt_widget stream. The Arr_rational_function_traits_2 class (see Section 31.6.6) and the Arr_linear_traits_2 class (see Section 31.6.2) currently do not provide this operator for the geometric types they define. Thus, only arrangements of line segments, polylines, or conic ards can be written. The << operator for polylines and conic arcs defined in CGAL/IO/Qt_widget_Polyline_2.h and CGAL/IO/Qt_widget_Conic_arc_2.h must be explicitly included, to insert polylines and conic arcs respectively into Qt_widget streams.
31.12 Adapting to Boost Graphs
Boost21 is a collection of portable C++ libraries that extend the Standard Template Library (Stl). The Boost Graph Library (bgl), which one of the libraries in the collection, offers an extensive set of generic graph algorithms parameterized through templates. As our arrangements are embedded as planar graphs, it is only natural to extend the underlying data structure with the interface that the bgl expects, and gain the ability to perform the operations that the bgl supports, such as shortest-path computation. This section describes how apply the graph algorithms implemented in the bgl to Arrangement_2 instances.
An instance of Arrangement_2 is adapted to a Boost graph through the provision of a set of free functions that operate on the arrangement features and conform with the relevant BGL concepts. Besides the straightforward adaptation, which associates a vertex with each Dcel vertex and an edge with each Dcel halfedge, the package also offer a dual adaptor, which associates a graph vertex with each Dcel face, such that two vertices are connected, iff there is a Dcel halfedge that connects the two corresponding faces.
31.12.1 The Primal Arrangement Representation
Arrangement instances are adapted to Boost graphs by specializing the boost:graph_traits template for Arrangement_2 instances. The graph-traits states the graph concepts that the arrangement class models (see below) and defines the types required by these concepts.
In this specialization the Arrangement_2 vertices correspond to the graph vertices, where two vertices are adjacent if there is at least one halfedge connecting them. More precisely, Arrangement_2::Vertex_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. As halfedges are directed, we consider the graph to be directed as well. Moreover, as several interior-disjoint x-monotone curves (say circular arcs) may share two common endpoints, inducing an arrangement with two vertices that are connected with several edges, we allow parallel edges in our Boost graph.
Given an Arrangement_2 instance, we can efficiently traverse its vertices and halfedges. Thus, the arrangement graph is a model of the concepts VertexListGraph and EdgeListGraph introduced by the bgl. At the same time, we use an iterator adapter of the circulator over the halfedges incident to a vertex (Halfedge_around_vertex_circulator - see Section 31.2.2.1), so it is possible to go over the ingoing and outgoing edges of a vertex in linear time. Thus, our arrangement graph is a model of the concept BidirectionalGraph (this concept refines IncidenceGraph, which requires only the traversal of outgoing edges).
It is important to notice that the vertex descriptors we use are Vertex_handle objects and not vertex indices. However, in order to gain more efficiency in most bgl algorithm, it is better to have them indexed 0, 1, … , (n-1), where n is the number of vertices. We therefore introduce the Arr_vertex_index_map<Arrangement> class-template, which maintains a mapping of vertex handles to indices, as required by the bgl. An instance of this class must be attached to a valid arrangement vertex when it is created. It uses the notification mechanism (see Section 31.7) to automatically maintain the mapping of vertices to indices, even when new vertices are inserted into the arrangement or existing vertices are removed.
In most algorithm provided by the bgl, the output is given by property maps, such that each map entry corresponds to a vertex. For example, when we compute the shortest paths from a given source vertex s to all other vertices we can obtain a map of distances and a map of predecessors - namely for each v vertex we have its distance from s and a descriptor of the vertex that precedes v in the shortest path from s. If the vertex descriptors are simply indices, one can use vectors to efficiently represent the property maps. As this is not the case with the arrangement graph, we offer the Arr_vertex_property_map<Arrangement,Type> template allows for an efficient mapping of Vertex_handle objects to properties of type Type. Note however that unlike the Arr_vertex_index_map class, the vertex property-map class is not kept synchronized with the number of vertices in the arrangement, so it should not be reused in calls to bgl functions in case the arrangement is modified in between these calls.
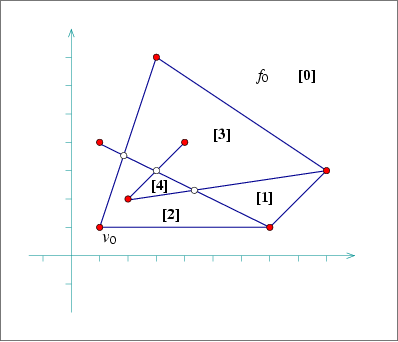
In the following example we construct an arrangement of 7 line segments, as shown in Figure 31.29, then use Dijkstra's shortest-paths algorithm from the bgl to compute the graph distance of all vertices from the leftmost vertex in the arrangement v0. Note the usage of the Arr_vertex_index_map and the Arr_vertex_property_map classes. The latter one, instantiated by the type double is used to map vertices to their distances from v0.
File: examples/Arrangement_on_surface_2/bgl_primal_adapter.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arrangement_2.h>
#include <CGAL/graph_traits_Arrangement_2.h>
#include <CGAL/Arr_vertex_index_map.h>
#include <climits>
#include <boost/graph/dijkstra_shortest_paths.hpp>
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arrangement_2<Traits_2> Arrangement_2;
// A functor used to compute the length of an edge.
class Edge_length_func
{
public:
// Boost property type definitions:
typedef boost::readable_property_map_tag category;
typedef double value_type;
typedef value_type reference;
typedef Arrangement_2::Halfedge_handle key_type;
double operator()(Arrangement_2::Halfedge_handle e) const
{
const double x1 = CGAL::to_double (e->source()->point().x());
const double y1 = CGAL::to_double (e->source()->point().y());
const double x2 = CGAL::to_double (e->target()->point().x());
const double y2 = CGAL::to_double (e->target()->point().y());
const double diff_x = x2 - x1;
const double diff_y = y2 - y1;
return std::sqrt(diff_x*diff_x + diff_y*diff_y);
}
};
double get(Edge_length_func edge_length, Arrangement_2::Halfedge_handle e)
{
return edge_length(e);
}
/* The folowing is a workaround for a bug in the BGL upto and including version
* 103400.
*
* Unfortunately some of the calls to the get() function below from the BGL
* code are qualified with the boost namespace, while others are not. For The
* qualified calls the compiler naturally looks for the definition of the
* function in boost namespace. For the other calls it searches the CGAL
* namespace according to ADL (Koenig Lookup), as the type of the 1st
* parameter is in CGAL namespace.
*
* One way to get around it is to provide 2 similar functions that do the
* same thing. One in CGAL namespace provided in CGAL/Arr_vertex_map.h, and
* the other in boost namespace below. The signature of the latter is slightly
* changed to avoid redefinition. The type of its 1st parameter is defined in
* boost namespace, and is a simple derivation of the 1st parameter of the
* CGAL::get() function.
*/
namespace boost {
template <typename Arrangement_2>
class Arr_vertex_index_map_boost :
public CGAL::Arr_vertex_index_map<Arrangement_2>
{
public:
typedef CGAL::Arr_vertex_index_map<Arrangement_2> Base;
/*! Default constructor. */
Arr_vertex_index_map_boost() : Base() {}
/*! Constructor from CGAL index map. */
Arr_vertex_index_map_boost(Base & other) :
CGAL::Arr_vertex_index_map<Arrangement_2>(other)
{}
};
/*!
* Get the index property-map function. Provided so that boost is able to
* access the Arr_vertex_index_map above.
* \param index_map The index map.
* \param v A vertex handle.
* \return The vertex index.
*/
template<class Arrangement>
unsigned int
get(const boost::Arr_vertex_index_map_boost<Arrangement> & index_map,
typename Arrangement::Vertex_handle v)
{
const CGAL::Arr_vertex_index_map<Arrangement> & index_map_tmp =
static_cast<const CGAL::Arr_vertex_index_map<Arrangement> &>(index_map);
return CGAL::get<Arrangement>(index_map_tmp, v);
}
}
int main()
{
Arrangement_2 arr;
// Construct an arrangement of seven intersecting line segments.
// We keep a handle for the vertex v_0 that corresponds to the point (1,1).
Arrangement_2::Halfedge_handle e =
insert_non_intersecting_curve (arr, Segment_2 (Point_2 (1, 1),
Point_2 (7, 1)));
Arrangement_2::Vertex_handle v0 = e->source();
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (3, 7)));
insert (arr, Segment_2 (Point_2 (1, 4), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (4, 4)));
insert (arr, Segment_2 (Point_2 (7, 1), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (3, 7), Point_2 (9, 3)));
// Create a mapping of the arrangement vertices to indices.
CGAL::Arr_vertex_index_map<Arrangement_2> index_map_tmp(arr);
boost::Arr_vertex_index_map_boost<Arrangement_2> index_map(index_map_tmp);
// Perform Dijkstra's algorithm from the vertex v0.
Edge_length_func edge_length;
CGAL::Arr_vertex_property_map<Arrangement_2, double> dist_map(index_map);
boost::dijkstra_shortest_paths(arr, v0,
boost::vertex_index_map(index_map).
weight_map(edge_length).
distance_map(dist_map));
// Print the results:
Arrangement_2::Vertex_iterator vit;
std::cout << "The distances of the arrangement vertices from ("
<< v0->point() << ") :" << std::endl;
for (vit = arr.vertices_begin(); vit != arr.vertices_end(); ++vit)
std::cout << "(" << vit->point() << ") at distance "
<< dist_map[vit] << std::endl;
return 0;
}
31.12.2 The Dual Arrangement Representation
It is possible to give a dual graph representation for an arrangement instance, such that each arrangement face corresponds to a graph vertex and two vertices are adjacent iff the corresponding faces share a common edge on their boundaries. This is done by specializing the boost:graph_traits template for Dual<Arrangement_2> instances, where Dual<Arrangement_2> is a template specialization that gives a dual interpretation to an arrangement instance.
In dual representation, Arrangement_2::Face_handle is the graph-vertex type, while Arrangement_2::Halfedge_handle is the graph-edge type. We treat the graph edges as directed, such that a halfedge e is directed from f1, which is its incident face, to f2, which is the incident face of its twin halfedge. As two arrangement faces may share more than a single edge on their boundary, we allow parallel edges in our Boost graph. As is the case in the primal graph, the dual arrangement graph is also a model of the concepts VertexListGraph, EdgeListGraph and BidirectionalGraph (thus also of IncidenceGraph).
Since we use Face_handle objects as the vertex descriptors, we define the Arr_face_index_map<Arrangement> class-template, which maintains an efficient mapping of face handles to indices. We also provide the template Arr_face_property_map<Arrangement,Type> for associating arbitrary data with the arrangement faces.
In the following example we construct the same arrangement as in example bgl_primal_adapter.cpp (see Figure 31.29), and perform breadth-first search on the graph faces, starting from the unbounded face. We extend the Dcel faces with an unsigned integer, marking the discover time of the face and use a breadth-first-search visitor to obtain these times and update the faces accordingly:
File: examples/Arrangement_on_surface_2/bgl_dual_adapter.cpp
#include "arr_rational_nt.h"
#include <CGAL/Cartesian.h>
#include <CGAL/Arr_segment_traits_2.h>
#include <CGAL/Arr_extended_dcel.h>
#include <CGAL/Arrangement_2.h>
#include <climits>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <CGAL/graph_traits_Dual_Arrangement_2.h>
#include <CGAL/Arr_face_index_map.h>
#include "arr_print.h"
typedef CGAL::Cartesian<Number_type> Kernel;
typedef CGAL::Arr_segment_traits_2<Kernel> Traits_2;
typedef Traits_2::Point_2 Point_2;
typedef Traits_2::X_monotone_curve_2 Segment_2;
typedef CGAL::Arr_face_extended_dcel<Traits_2,
unsigned int> Dcel;
typedef CGAL::Arrangement_2<Traits_2, Dcel> Arrangement_2;
typedef CGAL::Dual<Arrangement_2> Dual_arrangement_2;
// A BFS visitor class that associates each vertex with its discover time.
// In our case graph vertices represent arrangement faces.
template <class IndexMap>
class Discover_time_bfs_visitor : public boost::default_bfs_visitor
{
private:
const IndexMap *index_map; // Mapping vertices to indices.
unsigned int time; // The current time stamp.
public:
// Constructor.
Discover_time_bfs_visitor (const IndexMap& imap) :
index_map (&imap),
time (0)
{}
// Write the discover time for a given vertex.
template <typename Vertex, typename Graph>
void discover_vertex(Vertex u, const Graph& /* g */)
{
u->set_data (time);
time++;
}
};
int main ()
{
Arrangement_2 arr;
// Construct an arrangement of seven intersecting line segments.
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (1, 1), Point_2 (3, 7)));
insert (arr, Segment_2 (Point_2 (1, 4), Point_2 (7, 1)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (2, 2), Point_2 (4, 4)));
insert (arr, Segment_2 (Point_2 (7, 1), Point_2 (9, 3)));
insert (arr, Segment_2 (Point_2 (3, 7), Point_2 (9, 3)));
// Create a mapping of the arrangement faces to indices.
CGAL::Arr_face_index_map<Arrangement_2> index_map (arr);
// Perform breadth-first search from the unbounded face, and use the BFS
// visitor to associate each arrangement face with its discover time.
Discover_time_bfs_visitor<CGAL::Arr_face_index_map<Arrangement_2> >
bfs_visitor (index_map);
Arrangement_2::Face_handle uf = arr.unbounded_face();
boost::breadth_first_search (Dual_arrangement_2 (arr), uf,
boost::vertex_index_map (index_map).
visitor (bfs_visitor));
// Print the results:
Arrangement_2::Face_iterator fit;
for (fit = arr.faces_begin(); fit != arr.faces_end(); ++fit) {
std::cout << "Discover time " << fit->data() << " for ";
if (fit != uf) {
std::cout << "face ";
print_ccb<Arrangement_2> (fit->outer_ccb());
}
else
std::cout << "the unbounded face." << std::endl;
}
return 0;
}
31.13 How To Speed Up Your Computation
Before the specific tips, we remind you that compiling programs with debug flags disabled and with optimization flags enabled significantly reduces the running time.
- When the curves to be inserted into an arrangement are x-monotone
and pairwise disjoint in their interior to start with, then it is more
efficient (in running time) and less demanding (in traits-class
functionality) to use the non-intersection insertion-functions instead
of the general ones; e.g., insert().
- When the curves to be inserted into an arrangement are segments that
are pairwise disjoint in their interior, it is more efficient to use
the traits class Arr_non_caching_segment_traits_2 rather then
the default one (Arr_segment_traits_2).
If the segments may intersect each other, the default traits class Arr_segment_traits_2 can be safely used with the somehow limited number type Quotient<MP_float>.
On rare occasions the traits class Arr_non_caching_segment_traits_2 exhibits slightly better performance than the default one (Arr_segment_traits_2 even when the segments intersect each other, due to the small overhead of the latter (optimized) traits class. (For example, when the so called Leda rational kernel is used).
- Prior knowledge of the combinatorial structure of the arrangement can
be used to accelerate operations that insert x-monotone curves,
whose interior is disjoint from existing edges and vertices of the
arrangement. The specialized insertion functions, i.e.,
insert_in_face_interior(), insert_from_left_vertex(),
insert_from_right_vertex(), and insert_at_vertices()
can be used according to the available information. These functions
hardly involve any geometric operations, if at all. They accept
topologically related parameters, and use them to operate directly on
the Dcel records, thus saving algebraic operations, which are
especially expensive when high-degree curves are involved.
A polygon, represented by a list of segments along its boundary, can be inserted into an empty arrangement as follows. First, one segment is inserted using insert_in_face_interior() into the unbounded face. Then, a segment with a common end point is inserted using either insert_from_left_vertex() or insert_from_right_vertex(), and so on with the rest of the segments except for the last, which is inserted using insert_at_vertices(), as both endpoints of which are the mapping of known vertices.
- The main trade-off among point-location strategies, is between time
and storage. Using the naive or walk strategies, for example, takes
more query time but does not require preprocessing or maintenance of
auxiliary structures and saves storage space.
- If point-location queries are not performed frequently, but other
modifying functions, such as removing, splitting, or merging edges
are, then using a point-location strategy that does not require the
maintenance of auxiliary structures, such as the naive or walk
strategies, is preferable.
- There is a trade-off between two modes of the trapezoidal RIC strategy
that enables the user to choose whether preprocessing should be
performed or not. If preprocessing is not used, the creation of the
structure is faster. However, for some input sequences the structure
might be unbalanced and therefore queries and updates might take
longer, especially, if many removal and split operations are
performed.
- When the curves to be inserted into an arrangement are available in
advance (as opposed to supplied on-line), it is advised to use the
more efficient aggregate (sweep-based) insertion over the incremental
insertion; e.g., insert().
- The various traits classes should be instantiated with an exact number
type to ensure robustness, when the input of the operations to be
carried out might be degenerate, although inexact number types could
be used at the user's own risk.
- Maintaining short bit-lengths of coordinate representations may
drastically decrease the time consumption of arithmetic operations on
the coordinates. This can be achieved by caching certain information
or normalization (of rational numbers). However, both solutions should
be used cautiously, as the former may lead to an undue space
consumption, and indiscriminate normalization may considerably slow
down the overall process.
- Geometric functions (e.g., traits methods) dominate the time consumption of most operations. Thus, calls to such function should be avoided or at least their number should be decreased, perhaps at the expense of increased combinatorial-function calls or increased space consumption. For example, repetition of geometric-function calls could be avoided by storing the results obtained by the first call, and reusing them when needed.
Design and Implementation History
The code of this package is the result of a long development process. Initially (and until version 3.1), the code was spread among several components, namely, Topological_map, Planar_map_2, Planar_map_with_intersections_2 and Arrangement_2, that were developed by Ester Ezra, Eyal Flato, Efi Fogel, Dan Halperin, Iddo Hanniel, Idit Haran, Shai Hirsch, Eugene Lipovetsky, Oren Nechushtan, Sigal Raab, Ron Wein, Baruch Zukerman, and Tali Zvi.
In version 3.2, as part of the ACS project, the packages have gone through a major re-design, resulting in an improved and unified 2D Arrangements package. The code of the new package was restructured and developed by Efi Fogel, Idit Haran, Ron Wein, and Baruch Zukerman. This version included for the first time a new geometry-traits class that handles circular and linear curves, and is based on the circular kernel. The circular kernel was developed by Monique Teillaud, Sylvain Pion, and Julien Hazebrouck.
Version 3.3 features arrangements of unbounded curves for the first time. The design and development of this feature required yet another restructuring of the entire package. All this was done by Eric Berberich, Efi Fogel, Dan Halperin, Ophir Setter, and Ron Wein. Michael Hemmer helped tuning up parts of the geometry-traits concept related to unbounded curves.
Version 3.7 introduced a geometry-traits class that handles planar algebraic curves of arbitrary degree. It was developed by Eric Berberich and Michael Kerber.
Version 3.9 introduced a new geometry-traits class that handles rational arcs. It was developed by Oren Salzman and Michael Hemmer. It replaced an old traits, which handled the same family of curves, developed by Ron Wein.
Footnotes
| 1 | A continuous planar curve C is x-monotone if every vertical line intersects it at most once. For example, a non-vertical line segment is always x-monotone and so is the graph of any continuous function y = f(x). For convenience, we treat vertical line segments as weakly x-monotone, as there exists a single vertical line that overlaps them. A circle of radius r centered at (x0, y0) is not x-monotone, as the vertical line x = x0 intersects it at (x0, y0 - r) and at (x0, y0 + r). |
| 2 | The term parameter space stems from a major extension the arrangement package is going through to support arrangements embedded on certain two-dimensional parametric surfaces in three-dimensions (or higher). |
| 3 | A circulator is used to traverse a circular list, such as the list of halfedges incident to a vertex - see below. |
| 4 | The file arr_print.h, which can be found under the examples folder, includes this function and the rest of the functions listed in this section. Over there they are written in a more generic fashion, where the arrangement type serves as a template parameter for these functions, so different instantiations of the Arrangement_2<Traits,Dcel> template can be provided to the same function templates. |
| 5 | You may skip to Section 31.4, and return to this subsection at a later point in time. |
| 6 | Notice that in all figures in the rest of this chapter the coordinate axes are drawn only for illustrative purposes and are not part of the arrangement. |
| 7 | As a rule of thumb, one can use a bounded integer type for representing line segments whose coordinates are bounded by ⌊root3(M)⌋, where M is the maximal representable integer value. This guarantees that no overflows occur in the computations carried out by the traits class, hence all traits-class predicates always return correct results. |
| 8 | We use the term strategy following the design pattern taxonomy [GHJV95]. |
| 9 | The insert_non_intersecting_curve() function, as all other functions reviewed in this section, is a function template, parameterized by an arrangement class and a point-location class (a model of the ArrangementPointLocation_2 concept). |
| 10 | Note that a key operation performed by insert() is to locate the left endpoint of the curve in the arrangement. A circle, however, does not have any endpoints! |
| 11 | Currently, all point-location strategies except the trapezoidal RIC point-location strategy are capable of handling arrangements of unbounded curves. |
| 12 | If the two curves intersect at a point p but have different tangents, p is of multiplicity 1. If the tangents are also equal but the their curvatures are not the same, p is of multiplicity 2, etc. |
| 13 | We intend to enhance the arrangement template to handle curves confined to a bounded yet open parameter space. A curve that reaches the boundary of the parameter space in this case is bounded and open. |
| 14 | The tags Arr_oblivious_side_tag and Arr_open_side_tag are only two out of a larger number of options for the side categories included in major extension the code is going through. |
| 15 | We intend to introduce more concepts that require only a subset of the categories to be convertible to Arr_open_side_tag. |
| 16 | Many of the example programs in the rest of the chapter include a header file named arr_rational_nt.h, which defines a type named Number_type as either Gmpq or Quotient<MP_Float>, depending on whether Gmp is installed or not. |
| 17 | Namely, they are roots of polynomials with integer coefficients of degree 4. However, in some special cases, for example when handling only circles and circular arcs, the coordinates of the intersection points are only of degree 2, namely they are solutions of quadratic equations. |
| 18 | This curve can also be written as C: x2 + xy - y = 0. It is a hyperbola since ΔC = -1. |
| 19 | The term ``edge'' refers here to a pair of twin half-edges. |
| 20 | For simplicity, the particular observer used must be attached to an empty arrangement. It is not difficult however to modify the program to handle the general case of attaching a similar observer to a non-empty arrangement. |
| 21 | See also Boost's homepage at: www.boost.org. |