|
3 with edges parallel to the x,
y and z axis of the coordinate system.
Although they are represented in a canonical form by only two vertices, namely the lexicographically smallest and largest vertex with respect to Cartesian xyz coordinates, we provide functions for ``accessing'' the other vertices as well.
Iso-oriented cuboids and bounding boxes are quite similar. The difference however is that bounding boxes have always double coordinates, whereas the coordinate type of an iso-oriented cuboid is chosen by the user.
| Iso_cuboid_3<Kernel> c ( Point_3<Kernel> p, Point_3<Kernel> q); | |||
|
introduces an iso-oriented cuboid c with diagonal
opposite vertices p and q. Note that the object is
brought in the canonical form.
| |||
| Iso_cuboid_3<Kernel> c ( Point_3<Kernel> p, Point_3<Kernel> q, int); | |||
introduces an iso-oriented cuboid c with diagonal
opposite vertices p and q. The int argument value
is only used to distinguish the two overloaded functions.
| |||
| |||
|
introduces an iso-oriented cuboid c whose
minimal x coordinate is the one of left, the
maximal x coordinate is the one of right, the
minimal y coordinate is the one of bottom, the
maximal y coordinate is the one of top, the
minimal z coordinate is the one of far, the
maximal z coordinate is the one of close.
| |||
| |||
introduces an iso-oriented cuboid c with diagonal
opposite vertices
(min_hx/hw, min_hy/hw, min_hz/hw) and
(max_hx/hw, max_hy/hw, max_hz/hw).
| |||
| bool | c.operator== ( c2) const | Test for equality: two iso-oriented cuboid are equal, iff their lower left and their upper right vertices are equal. |
| bool | c.operator!= ( c2) const | Test for inequality. |
| Point_3<Kernel> | c.vertex ( int i) const | returns the i'th vertex modulo 8 of c. starting with the lower left vertex. |
| Point_3<Kernel> | c.operator[] ( int i) const | returns vertex(i), as indicated in the figure below: |
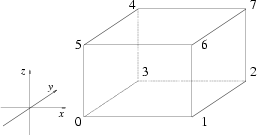
| Point_3<Kernel> | c.min () const | returns the smallest vertex of c (= vertex(0)). | ||
| Point_3<Kernel> | c.max () const | returns the largest vertex of c (= vertex(7)). | ||
| Kernel::FT | c.xmin () const | returns smallest Cartesian x-coordinate in c. | ||
| Kernel::FT | c.ymin () const | returns smallest Cartesian y-coordinate in c. | ||
| Kernel::FT | c.zmin () const | returns smallest Cartesian z-coordinate in c. | ||
| Kernel::FT | c.xmax () const | returns largest Cartesian x-coordinate in c. | ||
| Kernel::FT | c.ymax () const | returns largest Cartesian y-coordinate in c. | ||
| Kernel::FT | c.zmax () const | returns largest Cartesian z-coordinate in c. | ||
| Kernel::FT | c.min_coord ( int i) const |
returns i-th
Cartesian
coordinate of
the smallest vertex of c.
| ||
| Kernel::FT | c.max_coord ( int i) const |
returns i-th
Cartesian
coordinate of
the largest vertex of c.
|
| bool | c.is_degenerate () const | c is degenerate, if all vertices are coplanar. |
| Bounded_side | c.bounded_side ( Point_3<Kernel> p) const | |
| returns either ON_UNBOUNDED_SIDE, ON_BOUNDED_SIDE, or the constant ON_BOUNDARY, depending on where point p is. | ||
| bool | c.has_on_boundary ( Point_3<Kernel> p) const | |
| bool | c.has_on_bounded_side ( Point_3<Kernel> p) const | |
| bool | c.has_on_unbounded_side ( Point_3<Kernel> p) const | |
| Kernel::FT | c.volume () const | returns the volume of c. | ||
| Bbox_3 | c.bbox () const | returns a bounding box containing c. | ||
| Iso_cuboid_3<Kernel> | c.transform ( Aff_transformation_3<Kernel> t) const | |||
returns the iso-oriented cuboid obtained by applying t on
the smallest and the largest of c.
| ||||