|
CGAL 6.1 - 3D Alpha Shapes
|
|
CGAL 6.1 - 3D Alpha Shapes
|
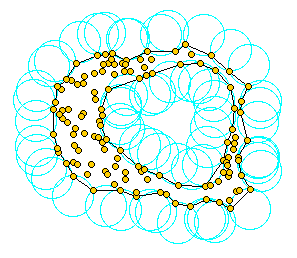
Assume we are given a set \( S\) of points in 2D or 3D and we would like to have something like "the shape formed by these points". This is quite a vague notion and there are probably many possible interpretations, the alpha shape being one of them. Alpha shapes can be used for shape reconstruction from a dense unorganized set of data points. Indeed, an alpha shape is demarcated by a frontier, which is a linear approximation of the original shape [1].
As mentioned in Edelsbrunner's and Mücke's paper [2], one can intuitively think of an alpha shape as the following. Imagine a huge mass of ice-cream making up the space \( \mathbb{R}^3\) and containing the points as "hard" chocolate pieces. Using one of those sphere-formed ice-cream spoons, we carve out all parts of the ice-cream block we can reach without bumping into chocolate pieces, thereby even carving out holes in the inside (e.g. parts not reachable by simply moving the spoon from the outside). We will eventually end up with a (not necessarily convex) object bounded by caps, arcs and points. If we now straighten all "round" faces to triangles and line segments, we have an intuitive description of what is called the alpha shape of \( S\). The drawing above provides an example of this process in 2D (where our ice-cream spoon is simply a circle).
Alpha shapes depend on a parameter \( \alpha\) after which they are named. In the ice-cream analogy above, \( \alpha\) is the squared radius of the carving spoon. A very small value will allow us to eat up all the ice-cream except the chocolate points themselves. Thus, we already see that the alpha shape degenerates to the point-set \( S\) for \( \alpha \rightarrow 0\). On the other hand, a huge value of \( \alpha\) will prevent us even from moving the spoon between two points since it is too large and we will never spoon up the ice-cream lying in the inside of the convex hull of \( S\). Hence, the alpha shape becomes the convex hull of \( S\) as \( \alpha \rightarrow \infty\).
CGAL offers 2D and 3D alpha shapes. The GUDHI library offers a dD Alpha complex.
We distinguish two versions of alpha shapes. Basic alpha shapes are based on the Delaunay triangulation. Weighted alpha shapes are based on its generalization, the regular triangulation (cf. Section Regular Triangulations), replacing the Euclidean distance by the power to weighted points.
Let us consider the basic case with a Delaunay triangulation. We first define the alpha complex of the set of points \( S\). The alpha complex is a subcomplex of the Delaunay triangulation. For a given value of \( \alpha\), the alpha complex includes all the simplices in the Delaunay triangulation which have an empty circumscribing sphere with squared radius equal or smaller than \( \alpha\). Here "empty" means that the open sphere does not include any points of \( S\). The alpha shape is then simply the domain covered by the simplices of the alpha complex (see [2]).
In general, an alpha complex is a disconnected and non-pure complex, meaning in particular that the alpha complex may have singular faces. For \( 0 \leq k \leq d-1\), a \( k\)-simplex of the alpha complex is said to be singular if it is not a facet of a \( (k+1)\)-simplex of the complex. CGAL provides two versions of alpha shapes. In the general mode, the alpha shapes correspond strictly to the above definition. The regularized mode provides a regularized version of the alpha shapes. It corresponds to the domain covered by a regularized version of the alpha complex where singular faces are removed (See Figure 54.1 for an example).

Figure 54.1 Comparison of general and regularized alpha-shape. Left: Some points are taken on the surface of a torus, three points being taken relatively far from the surface of the torus; Middle: The general alpha-shape (for a large enough alpha value) contains the singular triangle facet of the three isolated points; Right: The regularized version (for the same value of alpha) does not contain any singular facet.
The alpha shapes of a set of points \( S\) form a discrete family, even though they are defined for all real numbers \( \alpha\). The entire family of alpha shapes can be represented through the underlying triangulation of \( S\). In this representation each \( k\)-simplex of the underlying triangulation is associated with an interval that specifies for which values of \( \alpha\) the \( k\)-simplex belongs to the alpha complex. Relying on this fact, the family of alpha shapes can be computed efficiently and relatively easily. Furthermore, we can select the optimal value of \( \alpha\) to get an alpha shape including all data points and having less than a given number of connected components. Also, the alpha-values allows to define a filtration on the faces of the triangulation of a set of points. In this filtration, the faces of the triangulation are output in increasing order of the alpha value for which they appear in the alpha complex. In case of equal alpha values, lower dimensional faces are output first.
The definition is analog in the case of weighted alpha shapes. The input set is now a set of weighted points (which can be regarded as spheres) and the underlying triangulation is the regular triangulation of this set. Two spheres, or two weighted points, with centers \( C_1, C_2\) and radii \( r_1, r_2 \) are said to be orthogonal iff \( C_1C_2 ^2 = r_1^2 + r_2^2\) and suborthogonal iff \( C_1C_2 ^2 < r_1^2 + r_2^2\). For a given value of \( \alpha\), the weighted alpha complex is formed with the simplices of the regular triangulation such that there is a sphere orthogonal to the weighted points associated with the vertices of the simplex and suborthogonal to all the other input weighted points. Once again the alpha shape is then defined as the domain covered by the alpha complex and comes in general and regularized versions.
The class Alpha_shape_3<Dt,ExactAlphaComparisonTag> represents the whole family of alpha shapes for a given set of points. The class includes the underlying triangulation Dt of the set, and associates to each \( k\)-face of this triangulation an interval specifying for which values of \( \alpha\) the face belongs to the alpha complex. The second template parameter, ExactAlphaComparisonTag, is a tag that, when set to CGAL::Tag_true, triggers exact comparisons between alpha values.
The class provides functions to set and get the current \( \alpha\)-value, as well as an iterator that enumerates the \( \alpha\) values where the alpha shape changes.
Additionally, the class has a filtration member function that, given an output iterator with Object as value type, outputs the faces of the triangulation according to the order of apparition in the alpha complex when alpha increases.
Finally, it provides a function to determine the smallest value \( \alpha\) such that the alpha shape satisfies the following two properties:
The current implementation is static, that is after its construction points cannot be inserted or removed.
Given a value of alpha, the class Fixed_alpha_shape_3<Dt> represents one alpha shape for a given set of points. The class includes the underlying triangulation Dt of the set, and associates to each \( k\)-face of this triangulation a classification type. This class is dynamic, that is after its construction points can be inserted or removed.
Both classes provide member functions to classify for a (given) value of \( \alpha\) the different faces of the triangulation as EXTERIOR, SINGULAR, REGULAR or INTERIOR with respect to the alpha shape. A \( k\)-face on the boundary of the alpha complex is said to be: REGULAR if it is a subface of the alpha-complex which is a subface of a \( (k+1)\)-face of the alpha complex, and SINGULAR otherwise. A \( k\)-face of the alpha complex which is not on the boundary of the alpha complex is said to be INTERIOR. See Figure 54.2 for a 2D illustration.
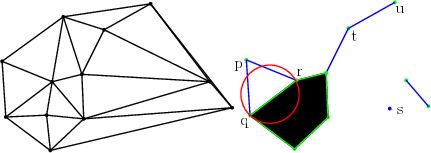
Figure 54.2 Classification of simplices, a 2D example. Left: The 2D Delaunay triangulation of a set of points; Right: Classification of simplices for a given alpha (the squared radius of the red circle). INTERIOR, REGULAR and SINGULAR simplices are depicted in black, green and blue respectively. EXTERIOR simplices are not depicted. The vertex s and the edge tu are SINGULAR since all higher dimension simplices they are incident to are EXTERIOR. The facet pqr is EXTERIOR because the squared radius of its circumscribed circle is larger than alpha.
The classes provide also output iterators to get for a given alpha value the vertices, edges, facets and cells of the different types (EXTERIOR, SINGULAR, REGULAR or INTERIOR).
It is possible to export a 3D alpha shape to a std::ostream using the operator<<, see the documentation of the class Alpha_shape_3 for more information.
We currently do not specify concepts for the underlying triangulation type. Models that work for a family of alpha-shapes are the instantiations of the classes Delaunay_triangulation_3 and Periodic_3_Delaunay_triangulation_3 (see example Example for Periodic Alpha Shapes). A model that works for a fixed alpha-shape are the instantiations of the class Delaunay_triangulation_3. Models that work for a weighted alpha-shape are the instantiations of the classes Regular_triangulation_3 and Periodic_3_regular_triangulation_3. The triangulation needs a geometric traits class and a triangulation data structure as template parameters.
For the class Alpha_shape_3<Dt,ExactAlphaComparisonTag>, the requirements of the traits class are described in the concepts AlphaShapeTraits_3 in the non-weighted case and WeightedAlphaShapeTraits_3 in the weighted case. All CGAL kernels are models of both concepts.
The triangulation data structure of the triangulation has to be a model of the concept TriangulationDataStructure_3 whose vertex and cell classes are model of the concepts AlphaShapeVertex_3 and AlphaShapeCell_3. The classes Alpha_shape_vertex_base_3<Gt> and Alpha_shape_cell_base_3<Gt> are models of these concepts and can be used for all type of alpha shapes, provided that the template parameters Vb and Fb are appropriately chosen, as we shall see in the following section.
For the class Fixed_alpha_shape_3<Dt>, the requirements of the traits class are described in the concepts FixedAlphaShapeTraits_3 in the non-weighted case and FixedWeightedAlphaShapeTraits_3 in the weighted case. All CGAL kernels are models of both concepts. The triangulation data structure of the triangulation has to be a model of the concept TriangulationDataStructure_3 whose vertex and cell classes are model of the concepts FixedAlphaShapeVertex_3 and FixedAlphaShapeCell_3. The package provides models Fixed_alpha_shape_vertex_base_3<Gt> and Fixed_alpha_shape_cell_base_3<Gt>, respectively.
Additional requirements are put when using weighted or periodic triangulations as underlying triangulation:
Regular_triangulation_3 or Periodic_3_regular_triangulation_3), the vertex and cell classes must respectively be models to both AlphaShapeVertex_3 and RegularTriangulationVertexBase_3, and to both AlphaShapeCell_3 and RegularTriangulationCellBase_3 (see example: Example for Weighted Alpha-Shapes). Periodic_3_Delaunay_triangulation_3 or Periodic_3_regular_triangulation_3), the vertex and cell classes must respectively be models to both AlphaShapeVertex_3 and Periodic_3TriangulationDSVertexBase_3, and to both AlphaShapeCell_3 and Periodic_3TriangulationDSCellBase_3 (see example: Example for Periodic Alpha Shapes). The class Alpha_shape_3<Dt,ExactAlphaComparisonTag> represents the whole family of alpha shapes for a given set of points while the class Fixed_alpha_shape_3<Dt> represents only one alpha shape (for a fixed alpha). When using the same kernel, Fixed_alpha_shape_3<Dt> is a lighter version. It is thus naturally much more efficient when the alpha-shape is needed for a single given value of alpha. In addition, note that the class Alpha_shape_3<Dt,ExactAlphaComparisonTag> requires constructions (squared radius of simplices) while the class Fixed_alpha_shape_3<Dt> uses only predicates. This implies that a certified construction of one (several) alpha-shape, using the Alpha_shape_3<Dt,ExactAlphaComparisonTag> requires a kernel with exact predicates and exact constructions (or setting ExactAlphaComparisonTag to Tag_true) while using a kernel with exact predicates is sufficient for the class Fixed_alpha_shape_3<Dt>. This makes the class Fixed_alpha_shape_3<Dt> even more efficient in this setting. In addition, note that the Fixed version is the only one of the two that supports incremental insertion and removal of points.
We give the time spent while computing the alpha shape of a protein (considered as a set of weighted points) featuring 4251 atoms (using gcc 4.3 under Linux with -O3 and -DNDEBUG flags, on a 2.27GHz Intel(R) Xeon(R) E5520 CPU): Using Exact_predicates_inexact_constructions_kernel, building the regular triangulation requires 0.09s, then the class Fixed_alpha_shape_3<Dt> required 0.05s while the class Alpha_shape_3<Dt,ExactAlphaComparisonTag> requires 0.35s if ExactAlphaComparisonTag is Tag_false (and 0.70s with Tag_true). Using Exact_predicates_exact_constructions_kernel, building the regular triangulation requires 0.19s and then the class Alpha_shape_3<Dt,ExactAlphaComparisonTag> requires 0.90s.
This example builds a basic alpha shape using a Delaunay triangulation as underlying triangulation.
File Alpha_shapes_3/ex_alpha_shapes_3.cpp
When many points are input in the alpha shape, say more than 10 000, it may pay off to use a Delaunay triangulation with the Fast_location policy as underlying triangulation in order to speed up point location queries (cf. Section The Location Policy Parameter).
File Alpha_shapes_3/ex_alpha_shapes_with_fast_location_3.cpp
The following examples build a weighted alpha shape requiring a regular triangulation as underlying triangulation. The alpha shape is built in GENERAL mode.
File Alpha_shapes_3/ex_weighted_alpha_shapes_3.cpp
Same example as previous but using a fixed value of alpha.
File Alpha_shapes_3/ex_fixed_weighted_alpha_shapes_3.cpp
On some platforms, the alpha shapes of the set of points of this example cannot be computed when using a traits with inexact constructions. To be able to compute them with a traits with inexact constructions, the tag ExactAlphaComparisonTag is set to Tag_true.
File Alpha_shapes_3/ex_alpha_shapes_exact_alpha.cpp
The following example shows how to use a periodic Delaunay triangulation (Chapter 3D Periodic Triangulations) as underlying triangulation for the alpha shape computation. Usage of a weighted Delaunay periodic triangulation is presented in the example: ex_weighted_periodic_alpha_shapes_3.cpp.
In order to define the original domain and to benefit from the built-in heuristic optimizations of the periodic triangulation computation, it is recommended to first construct the triangulation and then construct the alpha shape from it. The alpha shape constructor that takes a point range can be used as well but in this case the original domain cannot be specified and the default unit cube will be chosen and no optimizations will be used.
It is also recommended to switch the triangulation to 1-sheeted covering if possible. Note that a periodic triangulation in 27-sheeted covering space is degenerate. In this case, an exact constructions kernel needs to be used to compute the alpha shapes. Otherwise, the results will suffer from round-off problems.
File Alpha_shapes_3/ex_periodic_alpha_shapes_3.cpp