|
CGAL 4.12.1 - 2D Polygon Partitioning
|
|
CGAL 4.12.1 - 2D Polygon Partitioning
|
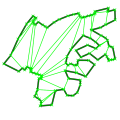
A partition of a polygon is a set of polygons such that the interiors of the polygons do not intersect and the union of the polygons is equal to the interior of the original polygon. Functions are available for partitioning planar polygons into two types of subpolygons (y-monotone polygons and convex polygons).
The function that produces a y-monotone partitioning is based on the algorithm presented in [1] which requires \( O(n \log n) \) time and \( O(n) \) space for a polygon with \( n \) vertices and guarantees nothing about the number of polygons produced with respect to the optimal number Three functions are provided for producing convex partitions. Two of these functions produce approximately optimal partitions and one results in an optimal partition, where optimal is defined in terms of the number of partition polygons. The two functions that implement approximation algorithms are guaranteed to produce no more than four times the optimal number of convex pieces. The optimal partitioning function provides an implementation of Greene's dynamic programming algorithm [2], which requires \( O(n^4) \) time and \( O(n^3) \) space to produce a convex partitioning. One of the approximation algorithms is also due to Greene [2] and requires \( O(n \log n) \) time and \( O(n) \) space to produce a convex partitioning given a y-monotone partitioning. The other approximation algorithm is a result of Hertel and Mehlhorn [3], which requires \( O(n) \) time and space to produce a convex partitioning from a triangulation of a polygon. Each of the partitioning functions uses a traits class to supply the primitive types and predicates used by the algorithms.
The assertion flags for this package use PARTITION in their names (e.g., CGAL_PARTITION_NO_POSTCONDITIONS). The precondition checks for the planar polygon partitioning functions are: counterclockwise ordering of the input vertices and simplicity of the polygon these vertices represent.
The postcondition checks are: simplicity, counterclockwise orientation, and convexity (or \( y\)-monotonicity) of the partition polygons and validity of the partition (i.e., the partition polygons are nonoverlapping and the union of these polygons is the same as the original polygon).
ConvexPartitionIsValidTraits_2IsYMonotoneTraits_2OptimalConvexPartitionTraits_2PartitionTraits_2PartitionIsValidTraits_2YMonotonePartitionIsValidTraits_2YMonotonePartitionTraits_2CGAL::Is_convex_2<Traits>CGAL::Is_vacuously_valid<Traits>CGAL::Is_y_monotone_2<Traits>CGAL::approx_convex_partition_2()CGAL::convex_partition_is_valid_2()CGAL::greene_approx_convex_partition_2()CGAL::is_y_monotone_2()CGAL::optimal_convex_partition_2()CGAL::partition_is_valid_2()CGAL::y_monotone_partition_2()CGAL::y_monotone_partition_is_valid_2() Modules | |
| Concepts | |
| Function Object Concepts | |
| Function Object Classes | |
Classes | |
| class | CGAL::Partition_is_valid_traits_2< Traits, PolygonIsValid > |
Class that derives a traits class for partition_is_valid_2() from a given traits class by defining the validity testing function object in terms of a supplied template parameter. More... | |
| class | CGAL::Partition_traits_2< R > |
| Traits class that can be used with all the 2-dimensional polygon partitioning algorithms. More... | |
Functions | |
| template<class InputIterator , class Traits > | |
| bool | CGAL::is_y_monotone_2 (InputIterator first, InputIterator beyond, const Traits &traits) |
determines if the sequence of points in the range [first, beyond) defines a \( y\)-monotone polygon or not. More... | |
| template<class InputIterator , class OutputIterator , class Traits > | |
| OutputIterator | CGAL::approx_convex_partition_2 (InputIterator first, InputIterator beyond, OutputIterator result, const Traits &traits=Default_traits) |
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons. More... | |
| template<class InputIterator , class OutputIterator , class Traits > | |
| OutputIterator | CGAL::greene_approx_convex_partition_2 (InputIterator first, InputIterator beyond, OutputIterator result, const Traits &traits=Default_traits) |
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons. More... | |
| template<class InputIterator , class OutputIterator , class Traits > | |
| OutputIterator | CGAL::optimal_convex_partition_2 (InputIterator first, InputIterator beyond, OutputIterator result, const Traits &traits=Default_traits) |
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons. More... | |
| template<class InputIterator , class OutputIterator , class Traits > | |
| OutputIterator | CGAL::y_monotone_partition_2 (InputIterator first, InputIterator beyond, OutputIterator result, const Traits &traits=Default_traits) |
computes a partition of the polygon defined by the points in the range [first, beyond) into \( y\)-monotone polygons. More... | |
| template<class InputIterator , class ForwardIterator , class Traits > | |
| bool | CGAL::convex_partition_is_valid_2 (InputIterator point_first, InputIterator point_beyond, ForwardIterator poly_first, ForwardIterator poly_beyond, const Traits &traits=Default_traits) |
determines if the polygons in the range [poly_first, poly_beyond) define a valid convex partition of the polygon defined by the points in the range [point_first, point_beyond). More... | |
| template<class InputIterator , class ForwardIterator , class Traits > | |
| bool | CGAL::partition_is_valid_2 (InputIterator point_first, InputIterator point_beyond, ForwardIterator poly_first, ForwardIterator poly_beyond, const Traits &traits=Default_traits) |
returns true iff the polygons in the range [poly_first, poly_beyond) define a valid partition of the polygon defined by the points in the range [point_first, point_beyond) and false otherwise. More... | |
| template<class InputIterator , class ForwardIterator , class Traits > | |
| bool | CGAL::y_monotone_partition_is_valid_2 (InputIterator point_first, InputIterator point_beyond, ForwardIterator poly_first, ForwardIterator poly_beyond, const Traits &traits=Default_traits) |
determines if the polygons in the range [poly_first, poly_beyond) define a valid \( y\)-monotone partition of the simple, counterclockwise-oriented polygon represented by the points in the range [point_first, point_beyond). More... | |
| OutputIterator CGAL::approx_convex_partition_2 | ( | InputIterator | first, |
| InputIterator | beyond, | ||
| OutputIterator | result, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_2.h>
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons.
The counterclockwise-oriented partition polygons are written to the sequence starting at position result. The past-the-end iterator for the resulting sequence of polygons is returned.
The number of convex polygons produced is no more than four times the minimal number.
first, beyond) define a simple counterclockwise-oriented polygon.Requirements
Traits is a model of the concept PartitionTraits_2 and, for the purposes of checking the postcondition that the partition produced is valid, it should also be a model of the concept ConvexPartitionIsValidTraits_2. std::iterator_traits<OutputIterator>::value_type should be Traits::Polygon_2. std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2. [first, beyond) must define a simple polygon whose vertices are oriented counterclockwise. The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator1>::value_type.
CGAL::convex_partition_is_valid_2() CGAL::greene_approx_convex_partition_2() CGAL::optimal_convex_partition_2() CGAL::partition_is_valid_2() CGAL::Partition_is_valid_traits_2<Traits, PolygonIsValid> CGAL::y_monotone_partition_2()Implementation
This function implements the algorithm of Hertel and Mehlhorn [3] and is based on the class Constrained_triangulation_2. Given a triangulation of the polygon, the function requires \( O(n)\) time and space for a polygon with \( n\) vertices.
Example
The following program computes an approximately optimal convex partitioning of a polygon using the default traits class and stores the partition polygons in the list partition_polys.
File Partition_2/approx_convex_partition_2.cpp
| bool CGAL::convex_partition_is_valid_2 | ( | InputIterator | point_first, |
| InputIterator | point_beyond, | ||
| ForwardIterator | poly_first, | ||
| ForwardIterator | poly_beyond, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_is_valid_2.h>
determines if the polygons in the range [poly_first, poly_beyond) define a valid convex partition of the polygon defined by the points in the range [point_first, point_beyond).
A convex partition is valid if the polygons do not overlap, the union of the polygons is the same as the original polygon given by the sequence of points, and if each partition polygon is convex. The function returns true iff the partition is valid and otherwise returns false.
point_first, point_beyond) define a simple, counterclockwise-oriented polygon.Requires
Traits is a model of the concept ConvexPartitionIsValidTraits_2.std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2.std::iterator_traits<ForwardIterator>::value_type should be Traits::Polygon_2.The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::approx_convex_partition_2() CGAL::greene_approx_convex_partition_2() CGAL::optimal_convex_partition_2() CGAL::partition_is_valid_2() CGAL::is_convex_2()Implementation
This function calls partition_is_valid_2() using the function object Is_convex_2 to determine the convexity of each partition polygon. Thus the time required by this function is \( O(n \log n + e \log e)\) where \( n\) is the total number of vertices in the partition polygons and \( e\) the total number of edges.
Example
See the example presented with the function approx_convex_partition_2() for an illustration of the use of this function.
| OutputIterator CGAL::greene_approx_convex_partition_2 | ( | InputIterator | first, |
| InputIterator | beyond, | ||
| OutputIterator | result, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_2.h>
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons.
The counterclockwise-oriented partition polygons are written to the sequence starting at position result. The number of convex polygons produced is no more than four times the minimal number. The past-the-end iterator for the resulting sequence of polygons is returned.
first, beyond) define a simple, counterclockwise-oriented polygon.Requirements
Traits is a model of the concepts PartitionTraits_2 and YMonotonePartitionTraits_2. For the purpose of checking the validity of the \( y\)-monotone partition produced as a preprocessing step for the convex partitioning, it must also be a model of YMonotonePartitionIsValidTraits_2. For the purpose of checking the postcondition that the convex partition is valid, Traits must also be a model of ConvexPartitionIsValidTraits_2. std::iterator_traits<OutputIterator>::value_type is equivalent to Traits::Polygon_2. std::iterator_traits<InputIterator>::value_type is equivalent to Traits::Point_2, which should also be equivalent to the type of the points stored in an object of type Traits::Polygon_2. The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::approx_convex_partition_2() CGAL::convex_partition_is_valid_2() CGAL::optimal_convex_partition_2() CGAL::partition_is_valid_2() CGAL::y_monotone_partition_2()Implementation
This function implements the approximation algorithm of Greene [2] and requires \( O(n \log n)\) time and \( O(n)\) space to produce a convex partitioning given a \( y\)-monotone partitioning of a polygon with \( n\) vertices. The function y_monotone_partition_2() is used to produce the monotone partition.
Example
The following program computes an approximately optimal convex partitioning of a polygon using the default traits class and stores the partition polygons in the list partition_polys.
File Partition_2/greene_approx_convex_partition_2.cpp
| bool CGAL::is_y_monotone_2 | ( | InputIterator | first, |
| InputIterator | beyond, | ||
| const Traits & | traits | ||
| ) |
#include <CGAL/is_y_monotone_2.h>
determines if the sequence of points in the range [first, beyond) defines a \( y\)-monotone polygon or not.
If so, the function returns true, otherwise it returns false.
Requires
Traits is a model of the concept IsYMonotoneTraits_2.std::iterator_traits<InputIterator>::value_type should be Traits::Point_2.The default traits class Default_traits is the kernel in which the type std::iterator_traits<InputIterator>::value_type is defined.
CGAL::Is_y_monotone_2<Traits> CGAL::y_monotone_partition_2() CGAL::y_monotone_partition_is_valid_2()Implementation
This function requires \( O(n)\) time for a polygon with \( n\) vertices.
Example
The following program computes a \( y\)-monotone partitioning of a polygon using the default traits class and stores the partition polygons in the list partition_polys. It then asserts that each of the partition polygons is, in fact, a \( y\)-monotone polygon and that the partition is valid. (Note that the assertions are superfluous unless the postcondition checking done by y_monotone_partition_2() has been turned off during compilation.)
File Partition_2/y_monotone_partition_2.cpp
| OutputIterator CGAL::optimal_convex_partition_2 | ( | InputIterator | first, |
| InputIterator | beyond, | ||
| OutputIterator | result, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_2.h>
computes a partition of the polygon defined by the points in the range [first, beyond) into convex polygons.
The counterclockwise-oriented partition polygons are written to the sequence starting at position result. The number of convex polygons produced is minimal. The past-the-end iterator for the resulting sequence of polygons is returned.
first, beyond) define a simple, counterclockwise-oriented polygon.Requirements
Traits is a model of the concept OptimalConvexPartitionTraits_2. For the purposes of checking the postcondition that the partition is valid, Traits should also be a model of ConvexPartitionIsValidTraits_2.
std::iterator_traits<OutputIterator>::value_type should be Traits::Polygon_2. std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2. The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::approx_convex_partition_2() CGAL::convex_partition_is_valid_2() CGAL::greene_approx_convex_partition_2() CGAL::partition_is_valid_2() CGAL::Partition_is_valid_traits_2<Traits, PolygonIsValid>Implementation
This function implements the dynamic programming algorithm of Greene [2], which requires \( O(n^4)\) time and \( O(n^3)\) space to produce a partitioning of a polygon with \( n\) vertices.
Example
The following program computes an optimal convex partitioning of a polygon using the default traits class and stores the partition polygons in the list partition_polys. It then asserts that the partition produced is valid. The traits class used for testing the validity is derived from the traits class used to produce the partition with the function object class Is_convex_2 used to define the required Is_valid type. (Note that this assertion is superfluous unless the postcondition checking for optimal_convex_partition_2() has been turned off.)
File Partition_2/optimal_convex_partition_2.cpp
| bool CGAL::partition_is_valid_2 | ( | InputIterator | point_first, |
| InputIterator | point_beyond, | ||
| ForwardIterator | poly_first, | ||
| ForwardIterator | poly_beyond, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_is_valid_2.h>
returns true iff the polygons in the range [poly_first, poly_beyond) define a valid partition of the polygon defined by the points in the range [point_first, point_beyond) and false otherwise.
A valid partition is one in which the polygons are nonoverlapping and the union of the polygons is the same as the original polygon. Each polygon must also satisfy the property tested by Traits::Is_valid().
point_first, point_beyond) define a simple, counterclockwise-oriented polygon.Requires
Traits is a model of the concept PartitionIsValidTraits_2 and the concept defining the requirements for the validity test implemented by Traits::Is_valid().std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2.std::iterator_traits<ForwardIterator>::value_type should be Traits::Polygon_2.The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::approx_convex_partition_2() CGAL::greene_approx_convex_partition_2() CGAL::is_y_monotone_2() CGAL::optimal_convex_partition_2() CGAL::Partition_is_valid_traits_2<Traits, PolygonIsValid> CGAL::y_monotone_partition_2() CGAL::is_convex_2()Implementation
This function requires \( O(n \log n + e \log e + \Sigma_{i=1}^p m_i)\) where \( n\) is the total number of vertices of the \( p\) partition polygons, \( e\) is the total number of edges of the partition polygons and \( m_i\) is the time required by Traits::Is_valid() to test if partition polygon \( p_i\) is valid.
Example
See the example presented with the function optimal_convex_partition_2() for an illustration of the use of this function.
| OutputIterator CGAL::y_monotone_partition_2 | ( | InputIterator | first, |
| InputIterator | beyond, | ||
| OutputIterator | result, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_2.h>
computes a partition of the polygon defined by the points in the range [first, beyond) into \( y\)-monotone polygons.
The counterclockwise-oriented partition polygons are written to the sequence starting at position result. The past-the-end iterator for the resulting sequence of polygons is returned.
first, beyond) define a simple, counterclockwise-oriented polygon.Requirements
Traits is a model of the concept YMonotonePartitionTraits_2 and, for the purposes of checking the postcondition that the partition is valid, it should also be a model of YMonotonePartitionIsValidTraits_2. std::iterator_traits<OutputIterator>::value_type should be Traits::Polygon_2. std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2. The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::approx_convex_partition_2() CGAL::greene_approx_convex_partition_2() CGAL::optimal_convex_partition_2() CGAL::partition_is_valid_2() CGAL::y_monotone_partition_is_valid_2()Implementation
This function implements the algorithm presented by de Berg et al. [1] which requires \( O(n \log n)\) time and \( O(n)\) space for a polygon with \( n\) vertices.
Example
The following program computes a \( y\)-monotone partitioning of a polygon using the default traits class and stores the partition polygons in the list partition_polys. It then asserts that each partition polygon produced is, in fact, \( y\)-monotone and that the partition is valid. (Note that these assertions are superfluous unless the postcondition checking for y_monotone_partition_2() has been turned off.)
File Partition_2/y_monotone_partition_2.cpp
| bool CGAL::y_monotone_partition_is_valid_2 | ( | InputIterator | point_first, |
| InputIterator | point_beyond, | ||
| ForwardIterator | poly_first, | ||
| ForwardIterator | poly_beyond, | ||
| const Traits & | traits = Default_traits |
||
| ) |
#include <CGAL/partition_is_valid_2.h>
determines if the polygons in the range [poly_first, poly_beyond) define a valid \( y\)-monotone partition of the simple, counterclockwise-oriented polygon represented by the points in the range [point_first, point_beyond).
A valid partition is one in which the polygons are nonoverlapping and the union of the polygons is the same as the original polygon and each polygon is \( y\)-monotone
true iff the partition is valid and otherwise returns false.Requires
Traits is a model of the concept YMonotonePartitionIsValidTraits_2.std::iterator_traits<InputIterator>::value_type should be Traits::Point_2, which should also be the type of the points stored in an object of type Traits::Polygon_2.std::iterator_traits<ForwardIterator>::value_type should be Traits::Polygon_2.The default traits class Default_traits is Partition_traits_2, with the representation type determined by std::iterator_traits<InputIterator>::value_type.
CGAL::y_monotone_partition_2() CGAL::is_y_monotone_2() CGAL::partition_is_valid_2() CGAL::Partition_is_valid_traits_2<Traits, PolygonIsValid>Implementation
This function uses the function partition_is_valid_2() together with the function object Is_y_monotone_2 to determine if each polygon is \( y\)-monotone or not. Thus the time required is \( O(n \log n + e \log e)\) where \( n\) is the total number of vertices of the partition polygons and \( e\) is the total number of edges.
Example
See the example presented with the function y_monotone_partition_2() for an illustration of the use of this function.